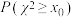名校
解题方法
1 . 袋中有8个除颜色外完全相同的小球,其中1个黑球,3个白球,4个红球.
(1)若从袋中一次性取出两个小球,即取到的红球个数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)若从袋中不放回的取3次,每次取一个小球,取到黑球记0分,取到白球记2分,取到红球记4分,在最终得分为8分的条件下,恰取到一个红球的概率.
(1)若从袋中一次性取出两个小球,即取到的红球个数为
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)若从袋中不放回的取3次,每次取一个小球,取到黑球记0分,取到白球记2分,取到红球记4分,在最终得分为8分的条件下,恰取到一个红球的概率.
您最近一年使用:0次
解题方法
2 . 下列说法中正确的是( )
A.若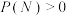 ,则 ,则 |
B.若 ,则 ,则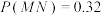 |
C.若随机变量 ,且 ,且 ,则 ,则 |
D.若随机变量 的分布列为 的分布列为 ,则 ,则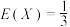 |
您最近一年使用:0次
名校
3 . 电视剧《庆余年2》自2024年5月16日在CCTV-8和腾讯视频双平台开播以来,其收视率一路飙升,《庆余年2》剧组为了解该剧的收视情况,在喜欢看电视的居民中随机抽取了1000名居民进行调查,其中,男性居民和女性居民人数之比为9:11,且观看本剧的居民比没有观看本剧的居民多800人,没有观看本剧的女性居民有50人.
(1)完成 列联表,并根据小概率值
列联表,并根据小概率值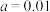 的独立性检验,能否认为是否观看《庆余年2》与性别有关联?
的独立性检验,能否认为是否观看《庆余年2》与性别有关联?
(2)在这1000名居民中,按性别比例用分层随机抽样的方法从看过《庆余年2》的居民中随机抽取9人,并从这9人中随机抽取3人采访其观剧感受,记这3人中男性居民的人数为X,求X的分布列和数学期望.
附: ,其中
,其中 .
.
(1)完成
 列联表,并根据小概率值
列联表,并根据小概率值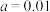 的独立性检验,能否认为是否观看《庆余年2》与性别有关联?
的独立性检验,能否认为是否观看《庆余年2》与性别有关联?男性居民 | 女性居民 | 总计 | |
看过《庆余年2》 | |||
没看过《庆余年2》 | 50 | ||
总计 | 1000 |
附:
 ,其中
,其中 .
.a | 0.01 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-07-13更新
|
487次组卷
|
4卷引用:河南省商丘市商师联盟2023-2024学年高二下学期7月期末联考数学试题
名校
解题方法
4 . 在2024年“市长杯”青少年校园足球联赛期间,市足球协会发起了“射手的连续进球与射手在球场上的区域位置有关系吗”的调查活动,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如下表所示:
(1)在所有参与调查的人中,用分层抽样的方法抽取 个人,已知从持“有关系”态度的人群中抽取了45人,求
个人,已知从持“有关系”态度的人群中抽取了45人,求 的值;
的值;
(2)在持“不知道”态度的人群中,用分层抽样的方法抽取10人看作一个总体.从这10人中随机选取3人,若设其中40岁以下的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
有关系 | 无关系 | 不知道 | |
40岁以下 | 800 | 450 | 200 |
40岁以上(含40岁) | 100 | 150 | 300 |
 个人,已知从持“有关系”态度的人群中抽取了45人,求
个人,已知从持“有关系”态度的人群中抽取了45人,求 的值;
的值;(2)在持“不知道”态度的人群中,用分层抽样的方法抽取10人看作一个总体.从这10人中随机选取3人,若设其中40岁以下的人数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
2024-06-28更新
|
248次组卷
|
2卷引用:河南省林州市第一中学2024-2025学年新高三7月调研考试数学试题
名校
解题方法
5 . 一个袋子中共有6个大小相同的球,其中3个红球,3个白球,从中随机摸出2个球,设取到白球的个数为X,则 的方差为
的方差为______ .
 的方差为
的方差为
您最近一年使用:0次
2024-06-22更新
|
268次组卷
|
5卷引用:河南省开封市五校2023-2024学年高二下学期4月期中联考数学试题
名校
6 . 2024年1月4日,教育部在京召开全国“双减”工作视频调度会,会议要求进一步提高双减政治站位,将“双减”工作作为重中之重,坚定不移推进,成为受老师和家长关注的重要话题.某学校为了解家长对双减工作的满意程度进行问卷调查(评价结果仅有“满意”、“不满意”),从所有参与评价的对象中随机抽取120人进行调查,部分数据如表所示(单位:人):
(1)请将 列联表补充完整,试根据小概率值
列联表补充完整,试根据小概率值 的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?
的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?
(2)若将频率视为概率,从所有给出“满意”的家长中随机抽取3人,用随机变量 表示被抽到的男性家长的人数,求
表示被抽到的男性家长的人数,求 的分布列;
的分布列;
(3)在抽出的120人中,从给出“满意”的家长中利用分层抽样的方法抽取10人,从给出“不满意”的对象中抽取 人.现从这
人.现从这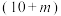 人中,随机抽出2人,用随机变量
人中,随机抽出2人,用随机变量 表示被抽到的给出“满意”的女性家长的人数.若随机变量
表示被抽到的给出“满意”的女性家长的人数.若随机变量 的数学期望不小于1,求
的数学期望不小于1,求 的最大值.
的最大值.
参考公式: ,其中
,其中 .
.
参考数据:
满意 | 不满意 | 合计 | |
男性 | 10 | 50 | |
女性 | 60 | ||
合计 | 120 |
 列联表补充完整,试根据小概率值
列联表补充完整,试根据小概率值 的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?
的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?(2)若将频率视为概率,从所有给出“满意”的家长中随机抽取3人,用随机变量
 表示被抽到的男性家长的人数,求
表示被抽到的男性家长的人数,求 的分布列;
的分布列;(3)在抽出的120人中,从给出“满意”的家长中利用分层抽样的方法抽取10人,从给出“不满意”的对象中抽取
 人.现从这
人.现从这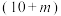 人中,随机抽出2人,用随机变量
人中,随机抽出2人,用随机变量 表示被抽到的给出“满意”的女性家长的人数.若随机变量
表示被抽到的给出“满意”的女性家长的人数.若随机变量 的数学期望不小于1,求
的数学期望不小于1,求 的最大值.
的最大值.参考公式:
 ,其中
,其中 .
.参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-05-08更新
|
737次组卷
|
5卷引用:河南省百师联盟联考2023-2024学年高二下学期6月联考数学试题
河南省百师联盟联考2023-2024学年高二下学期6月联考数学试题吉林省长春市第八中学2023-2024学年高二下学期第一次月考数学试题(已下线)第八章:成对数据的统计分析章末综合检测卷(新题型)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)专题07 回归方程与独立性检验--高二期末考点大串讲(苏教版2019选择性必修第二册)吉林省长春市文理高中2023-2024学年高二下学期5月月考数学试题
名校
7 . 某市组织宣传小分队进行法律法规宣传,某宣传小分队记录了前9天每天普及的人数,得到下表:
(1)从这9天的数据中任选4天的数据,以 表示4天中每天普及人数不少于240人的天数,求
表示4天中每天普及人数不少于240人的天数,求 的分布列和数学期望;
的分布列和数学期望;
(2)由于统计人员的疏忽,第5天的数据统计有误,如果去掉第5天的数据,试用剩下的数据求出每天普及的人数y关于天数 的线性回归方程.
的线性回归方程.
(参考数据:
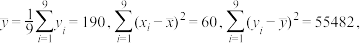
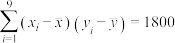 ,
,
附:对于一组数据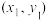 ,
,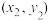 ,
, ,
, ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: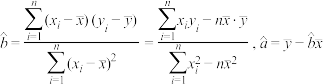 ).
).
时间 (天) (天) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 每天普及的人数y | 80 | 98 | 129 | 150 | 203 | 190 | 258 | 292 | 310 |
 表示4天中每天普及人数不少于240人的天数,求
表示4天中每天普及人数不少于240人的天数,求 的分布列和数学期望;
的分布列和数学期望;(2)由于统计人员的疏忽,第5天的数据统计有误,如果去掉第5天的数据,试用剩下的数据求出每天普及的人数y关于天数
 的线性回归方程.
的线性回归方程.(参考数据:
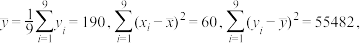
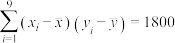 ,
,附:对于一组数据
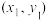 ,
,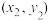 ,
, ,
, ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: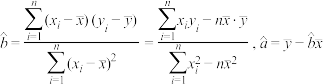 ).
).
您最近一年使用:0次
2024-04-08更新
|
1293次组卷
|
5卷引用:河南省安阳市2024届高三第三次模拟考试数学试题
河南省安阳市2024届高三第三次模拟考试数学试题湖南省常德市2024届高三下学期3月模拟考试数学试题 (已下线)第八章:成对数据的统计分析章末重点题型复习(5题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)8.5 二项分布、超几何分布与正态分布(高考真题素材之十年高考)山西省长治市第一中学校2023-2024学年高二下学期第二次段考数学试题
8 . 某学校共有1000名学生参加知识竞赛,其中男生400人,为了解该校学生在知识竞赛中的情况,采取分层抽样随机抽取了100名学生进行调查,分数分布在 分之间,根据调查的结果绘制的学生分数频率分布直方图如图所示:
分之间,根据调查的结果绘制的学生分数频率分布直方图如图所示:
(1)求 的值,并估计该校学生分数的平均数、中位数和众数(同一组中的数据用该组区间的中点值作代表);
的值,并估计该校学生分数的平均数、中位数和众数(同一组中的数据用该组区间的中点值作代表);
(2)现采用分层抽样的方式从分数落在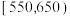 ,
,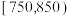 内的两组学生中抽取10人,再从这10人中随机抽取3人,记被抽取的3名学生中属于“高分选手”的学生人数为随机变量
内的两组学生中抽取10人,再从这10人中随机抽取3人,记被抽取的3名学生中属于“高分选手”的学生人数为随机变量 ,求
,求 的分布列及数学期望;
的分布列及数学期望;
 分之间,根据调查的结果绘制的学生分数频率分布直方图如图所示:
分之间,根据调查的结果绘制的学生分数频率分布直方图如图所示: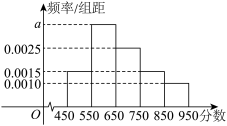
(1)求
 的值,并估计该校学生分数的平均数、中位数和众数(同一组中的数据用该组区间的中点值作代表);
的值,并估计该校学生分数的平均数、中位数和众数(同一组中的数据用该组区间的中点值作代表);(2)现采用分层抽样的方式从分数落在
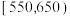 ,
,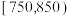 内的两组学生中抽取10人,再从这10人中随机抽取3人,记被抽取的3名学生中属于“高分选手”的学生人数为随机变量
内的两组学生中抽取10人,再从这10人中随机抽取3人,记被抽取的3名学生中属于“高分选手”的学生人数为随机变量 ,求
,求 的分布列及数学期望;
的分布列及数学期望;
您最近一年使用:0次
2024-01-18更新
|
777次组卷
|
6卷引用:河南省郑州市宇华实验学校2024届高三下学期开学摸底考试数学试题
河南省郑州市宇华实验学校2024届高三下学期开学摸底考试数学试题广东省广州美术学院附属中等美术学校2024届高三上学期期末数学试题(已下线)第07讲 7.4.2超几何分布-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)7.4.2 超几何分布——课后作业(基础版)(已下线)专题3.3二项分布与超几何分布(六个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)新疆阿勒泰地区2023-2024学年高二下学期期末联考数学试卷
9 . 在一个袋中装有除颜色外其余完全一样的3个黑球,3个白球,现从中任取4个球,设这4个球中黑球的个数为 ,则( )
,则( )
 ,则( )
,则( )A. 服从二项分布 服从二项分布 | B. 的值最小为1 的值最小为1 |
C. | D.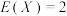 |
您最近一年使用:0次
解题方法
10 . 学校要从5名男生和2名女生中随机抽取2人参加社区志愿者服务,若用X表示抽取的志愿者中女生的人数,
(1)求抽取的2人恰有1个女生的概率;
(2)请写出随机变量 的分布列、数学期望
的分布列、数学期望 与方差
与方差 .
.
(1)求抽取的2人恰有1个女生的概率;
(2)请写出随机变量
 的分布列、数学期望
的分布列、数学期望 与方差
与方差 .
.
您最近一年使用:0次
2024-06-15更新
|
464次组卷
|
3卷引用:河南省洛阳市新安县职业高级中学 2023-2024学年高二下学期期末考试数学试卷
河南省洛阳市新安县职业高级中学 2023-2024学年高二下学期期末考试数学试卷广东省东莞市长安中学等七校2022-2023学年高二下学期期中联考数学试卷(已下线)第2套 全真模拟卷 (基础)【高二期末复习全真模拟】