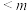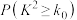1 . (1)为了解中草药甲对某疾病的预防效果,研究人员随机调查了100名人员,调查数据如表.(单位:个)若规定显著性水平 ,试分析中草药甲对预防此疾病是否有效;
,试分析中草药甲对预防此疾病是否有效;
(2)已知一个盒子中装有大小和质地相同的6个红球和3个白球.现从盒子中不放回地依次随机取出2个球,设2个球中红球的个数为X,求X的分布列、期望和方差.
附: ,
, .
.
 ,试分析中草药甲对预防此疾病是否有效;
,试分析中草药甲对预防此疾病是否有效;| 未患病者 | 患病者 | 合计 | |
| 未服用 中草药甲 | 29 | 16 | 45 |
| 服用 中草药甲 | 46 | 9 | 55 |
| 合计 | 75 | 25 | 100 |
附:
 ,
, .
.| α | 0.100 | 0.050 | 0.010 | 0.001 |
| x | 2.706 | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
名校
2 . 治疗某种疾病有一种传统药和一种创新药,治疗效果对比试验数据如下:服用创新药的50名患者中有40名治愈;服用传统药的400名患者中有120名未治愈.
(1)补全 列联表(单位:人),并根据小概率值
列联表(单位:人),并根据小概率值 的独立性检验,分析创新药的疗效是否比传统的疗效药好;
的独立性检验,分析创新药的疗效是否比传统的疗效药好;
(2)从服用传统药的400名患者中按疗效比例分层随机抽取10名,在这10人中随机抽取8人进行回访,用 表示回访中治愈者的人数,求
表示回访中治愈者的人数,求 的分布列及均值.
的分布列及均值.
附: ,
,
(1)补全
 列联表(单位:人),并根据小概率值
列联表(单位:人),并根据小概率值 的独立性检验,分析创新药的疗效是否比传统的疗效药好;
的独立性检验,分析创新药的疗效是否比传统的疗效药好;| 药物 | 疗效 | 合计 | |
| 治愈 | 未治愈 | ||
| 创新药 | |||
| 传统药 | |||
| 合计 | |||
(2)从服用传统药的400名患者中按疗效比例分层随机抽取10名,在这10人中随机抽取8人进行回访,用
 表示回访中治愈者的人数,求
表示回访中治愈者的人数,求 的分布列及均值.
的分布列及均值.附:
 ,
, | 0.1 | 0.05 | 0.01 |
 | 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
2024-05-14更新
|
1198次组卷
|
3卷引用:上海市延安中学2023-2024学年高二下学期期末考试数学试卷
名校
3 . 刷脸时代来了,人们为“刷脸支付”给生活带来的便捷感到高兴,但“刷脸支付”的安全性也引起了人们的担忧.某调查机构为了解人们对“刷脸支付”的接受程度,通过安全感问卷进行调查(问卷得分在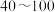 分之间),并从参与者中随机抽取
分之间),并从参与者中随机抽取 人.根据调查结果绘制出如图所示的频率分布直方图.
人.根据调查结果绘制出如图所示的频率分布直方图.
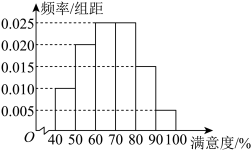
(1)据此估计这 人满意度的平均数
人满意度的平均数 同一组中的数据用该组区间的中点值作代表
同一组中的数据用该组区间的中点值作代表 ;
;
(2)某大型超市引入“刷脸支付”后,在推广“刷脸支付”期间,推出两种付款方案:方案一:不采用“刷脸支付”,无任何优惠,但可参加超市的抽奖返现金活动.活动方案为:从装有 个形状、大小完全相同的小球
个形状、大小完全相同的小球 其中红球
其中红球 个,黑球
个,黑球 个
个 的抽奖盒中,一次性摸出
的抽奖盒中,一次性摸出 个球,若摸到
个球,若摸到 个红球,返消费金额的
个红球,返消费金额的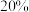 ;若摸到
;若摸到 个红球,返消费金额的
个红球,返消费金额的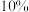 ,除此之外不返现金.
,除此之外不返现金.
方案二:采用“刷脸支付”,此时对购物的顾客随机优惠,但不参加超市的抽奖返现金活动,根据统计结果得知,使用“刷脸支付”时有 的概率享受
的概率享受 折优惠,有
折优惠,有 的概率享受
的概率享受 折优惠,有
折优惠,有 的概率享受
的概率享受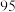 折优惠.现小张在该超市购买了总价为
折优惠.现小张在该超市购买了总价为 元的商品.
元的商品.
①求小张选择方案一付款时实际付款额 的分布列与数学期望;
的分布列与数学期望;
②试从期望角度,比较小张选择方案一与方案二付款,哪个方案更划算?(注:结果精确到 )
)
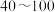 分之间),并从参与者中随机抽取
分之间),并从参与者中随机抽取 人.根据调查结果绘制出如图所示的频率分布直方图.
人.根据调查结果绘制出如图所示的频率分布直方图.
(1)据此估计这
 人满意度的平均数
人满意度的平均数 同一组中的数据用该组区间的中点值作代表
同一组中的数据用该组区间的中点值作代表 ;
;(2)某大型超市引入“刷脸支付”后,在推广“刷脸支付”期间,推出两种付款方案:方案一:不采用“刷脸支付”,无任何优惠,但可参加超市的抽奖返现金活动.活动方案为:从装有
 个形状、大小完全相同的小球
个形状、大小完全相同的小球 其中红球
其中红球 个,黑球
个,黑球 个
个 的抽奖盒中,一次性摸出
的抽奖盒中,一次性摸出 个球,若摸到
个球,若摸到 个红球,返消费金额的
个红球,返消费金额的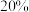 ;若摸到
;若摸到 个红球,返消费金额的
个红球,返消费金额的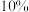 ,除此之外不返现金.
,除此之外不返现金.方案二:采用“刷脸支付”,此时对购物的顾客随机优惠,但不参加超市的抽奖返现金活动,根据统计结果得知,使用“刷脸支付”时有
 的概率享受
的概率享受 折优惠,有
折优惠,有 的概率享受
的概率享受 折优惠,有
折优惠,有 的概率享受
的概率享受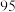 折优惠.现小张在该超市购买了总价为
折优惠.现小张在该超市购买了总价为 元的商品.
元的商品.①求小张选择方案一付款时实际付款额
 的分布列与数学期望;
的分布列与数学期望;②试从期望角度,比较小张选择方案一与方案二付款,哪个方案更划算?(注:结果精确到
 )
)
您最近一年使用:0次
2024-04-30更新
|
1878次组卷
|
7卷引用:上海市金山中学2023-2024学年高二下学期5月月考数学试卷
上海市金山中学2023-2024学年高二下学期5月月考数学试卷宁夏回族自治区石嘴山市平罗中学2024届高三下学期第三次模拟考试数学(理)试题(已下线)9.1 随机抽样与统计图标(高考真题素材之十年高考)湖南省长沙市长郡中学2024届高三下学期模拟(三)数学试题(已下线)专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)辽宁省沈阳市东北育才学校2024届高三考前最后一模数学试题广东省茂名市高州中学2025届高三上学期8月月考数学试题
名校
4 . 某商店随机抽取了当天100名客户的消费金额,并分组如下: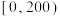 ,
,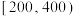 ,
,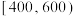 ,…,
,…,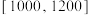 (单位:元),得到如图所示的频率分布直方图.
(单位:元),得到如图所示的频率分布直方图.
(2)若利用分层随机抽样的方法从消费不少于800元的客户中共抽取6人,再从这6人中随机抽取2人做进一步调查,则抽到的2人中至少有1人的消费金额不少于1000元的概率是多少;
(3)为吸引顾客消费,该商店考虑两种促销方案.方案一:消费金额每满300元可立减50元,并可叠加使用;方案二:消费金额每满1000元即可抽奖三次,每次中奖的概率均为 ,且每次抽奖互不影响.中奖1次当天消费金额可打9折,中奖2次当天消费金额可打6折,中奖3次当天消费金额可打3折.若两种方案只能选择其中一种,小王准备购买的商品又恰好标价1000元,请帮助他选择合适的促销方案并说明理由.
,且每次抽奖互不影响.中奖1次当天消费金额可打9折,中奖2次当天消费金额可打6折,中奖3次当天消费金额可打3折.若两种方案只能选择其中一种,小王准备购买的商品又恰好标价1000元,请帮助他选择合适的促销方案并说明理由.
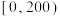 ,
,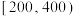 ,
,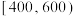 ,…,
,…,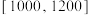 (单位:元),得到如图所示的频率分布直方图.
(单位:元),得到如图所示的频率分布直方图.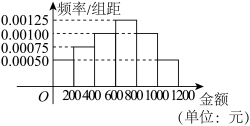
(2)若利用分层随机抽样的方法从消费不少于800元的客户中共抽取6人,再从这6人中随机抽取2人做进一步调查,则抽到的2人中至少有1人的消费金额不少于1000元的概率是多少;
(3)为吸引顾客消费,该商店考虑两种促销方案.方案一:消费金额每满300元可立减50元,并可叠加使用;方案二:消费金额每满1000元即可抽奖三次,每次中奖的概率均为
 ,且每次抽奖互不影响.中奖1次当天消费金额可打9折,中奖2次当天消费金额可打6折,中奖3次当天消费金额可打3折.若两种方案只能选择其中一种,小王准备购买的商品又恰好标价1000元,请帮助他选择合适的促销方案并说明理由.
,且每次抽奖互不影响.中奖1次当天消费金额可打9折,中奖2次当天消费金额可打6折,中奖3次当天消费金额可打3折.若两种方案只能选择其中一种,小王准备购买的商品又恰好标价1000元,请帮助他选择合适的促销方案并说明理由.
您最近一年使用:0次
2024-04-01更新
|
1054次组卷
|
7卷引用:上海市浦东新区2024届高三下学期期中教学质量检测数学试卷
上海市浦东新区2024届高三下学期期中教学质量检测数学试卷上海市新川中学2023-2024学年高二下学期期中考试数学试题上海市南洋中学2023-2024学年高二下学期期末数学试题(已下线)第七章 随机变量及其分布总结 第二练 数学思想训练(已下线)第七章 随机变量及其分布(提升卷)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)山东省青岛第九中学2023-2024学年高二下学期期中阶段检测数学试题(已下线)第五章 概率统计创新问题 专题四 概率统计中的开放题 微点2 概率统计中的开放题综合训练【基础版】
名校
解题方法
5 . 为深入学习贯彻党的二十大精神,推动全市党员干部群众用好“学习强国”学习平台,激发干事创业热情.某单位组织“学习强国”知识竞赛,竞赛共有 道题目,随机抽取
道题目,随机抽取 道让参赛者回答.已知小明只能答对其中的
道让参赛者回答.已知小明只能答对其中的 道,试求:
道,试求:
(1)抽到他能答对题目数 的分布列;
的分布列;
(2)求 的期望和方差
的期望和方差
 道题目,随机抽取
道题目,随机抽取 道让参赛者回答.已知小明只能答对其中的
道让参赛者回答.已知小明只能答对其中的 道,试求:
道,试求:(1)抽到他能答对题目数
 的分布列;
的分布列;(2)求
 的期望和方差
的期望和方差
您最近一年使用:0次
2024-03-19更新
|
2681次组卷
|
10卷引用:上海市位育中学2023-2024学年高二下学期3月月考数学试卷
上海市位育中学2023-2024学年高二下学期3月月考数学试卷(已下线)专题07概率初步(续)全章复习攻略--高二期末考点大串讲(沪教版2020选修)(已下线)第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)8.2 离散型随机变量及其分布列(3)河北省沧州市吴桥县吴桥中学2023-2024学年高二下学期3月月考数学试题江苏省无锡市运河实验学校2023-2024学年高二下学期期中考试数学试卷(已下线)第七章:随机变量及其分布章末重点题型复习(7题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)江苏高二专题08概率与统计(第二部分)浙江省学军中学紫金港校区2023-2024学年高二下学期期中数学试题(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点1 重要的概率分布模型(一)【基础版】
23-24高三上·北京西城·期末
名校
解题方法
6 . 生活中人们喜爱用跑步软件记录分享自己的运动轨迹.为了解某地中学生和大学生对跑步软件的使用情况,从该地随机抽取了200名中学生和80名大学生,统计他们最喜爱使用的一款跑步软件,结果如下:
假设大学生和中学生对跑步软件的喜爱互不影响.
(1)从该地区的中学生和大学生中各随机抽取1人,用频率估计概率,试估计这2人都最喜爱使用跑步软件一的概率;
(2)采用分层抽样的方式先从样本中的大学生中随机抽取 人,再从这
人,再从这 人中随机抽取
人中随机抽取 人.记
人.记 为这
为这 人中最喜爱使用跑步软件二的人数,求
人中最喜爱使用跑步软件二的人数,求 的分布列和数学期望;
的分布列和数学期望;
(3)记样本中的中学生最喜爱使用这四款跑步软件的频率依次为 ,
, ,
, ,
, ,其方差为
,其方差为 ;样本中的大学生最喜爱使用这四款跑步软件的频率依次为
;样本中的大学生最喜爱使用这四款跑步软件的频率依次为 ,
, ,
,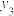 ,
,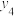 ,其方差为
,其方差为 ;
; ,
, ,
, ,
, ,
, ,
, ,
,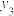 ,
,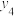 的方差为
的方差为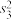 .写出
.写出 ,
, ,
,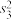 的大小关系.(结论不要求证明)
的大小关系.(结论不要求证明)
跑步软件一 | 跑步软件二 | 跑步软件三 | 跑步软件四 | |
中学生 | 80 | 60 | 40 | 20 |
大学生 | 30 | 20 | 20 | 10 |
(1)从该地区的中学生和大学生中各随机抽取1人,用频率估计概率,试估计这2人都最喜爱使用跑步软件一的概率;
(2)采用分层抽样的方式先从样本中的大学生中随机抽取
 人,再从这
人,再从这 人中随机抽取
人中随机抽取 人.记
人.记 为这
为这 人中最喜爱使用跑步软件二的人数,求
人中最喜爱使用跑步软件二的人数,求 的分布列和数学期望;
的分布列和数学期望;(3)记样本中的中学生最喜爱使用这四款跑步软件的频率依次为
 ,
, ,
, ,
, ,其方差为
,其方差为 ;样本中的大学生最喜爱使用这四款跑步软件的频率依次为
;样本中的大学生最喜爱使用这四款跑步软件的频率依次为 ,
, ,
,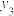 ,
,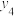 ,其方差为
,其方差为 ;
; ,
, ,
, ,
, ,
, ,
, ,
,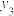 ,
,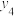 的方差为
的方差为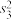 .写出
.写出 ,
, ,
,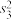 的大小关系.(结论不要求证明)
的大小关系.(结论不要求证明)
您最近一年使用:0次
2024-01-19更新
|
1751次组卷
|
7卷引用:上海市普陀区晋元高级中学2024届高三上学期秋考模拟数学试题
上海市普陀区晋元高级中学2024届高三上学期秋考模拟数学试题(已下线)2024年高考数学二轮复习测试卷(上海专用)上海市上海师范大学附属外国语学校2024届高三热身考试数学试卷(已下线)北京市西城区2024届高三上学期期末数学试题北京市西城区2024届高三上学期期末数学试题(已下线)专题21 概率与统计的综合运用(13大题型)(练习)(已下线)专题8-2分布列综合归类-1
23-24高二上·上海·课后作业
解题方法
7 . 从4名男生和2名女生中任选3人参加演讲比赛,设随机变量X表示所选3人中女生的人数.求:
(1)X的分布;
(2)X的期望与方差;
(3)“所选3人中女生人数 ”的概率.
”的概率.
(1)X的分布;
(2)X的期望与方差;
(3)“所选3人中女生人数
 ”的概率.
”的概率.
您最近一年使用:0次
解题方法
8 . 从4名男生和2名女生中任选3人参加演讲比赛,设随机变量X表示所选3人中女生的人数,求:
(1)“所选3人中女生人数 ”的概率;
”的概率;
(2)X的期望与方差.
(1)“所选3人中女生人数
 ”的概率;
”的概率;(2)X的期望与方差.
您最近一年使用:0次
名校
解题方法
9 . 某大学 学院共有学生1000人,其中男生640人,女生360人.该学院体育社团为了解学生参与跑步运动的情况,按性别分层抽样,从该学院所有学生中抽取若干人作为样本,对样本中的每位学生在5月份的累计跑步里程进行统计,得到下表.
学院共有学生1000人,其中男生640人,女生360人.该学院体育社团为了解学生参与跑步运动的情况,按性别分层抽样,从该学院所有学生中抽取若干人作为样本,对样本中的每位学生在5月份的累计跑步里程进行统计,得到下表.
(1)求 的值,并估计
的值,并估计 学院学生5月份累计跑步里程
学院学生5月份累计跑步里程 在
在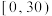 中的男生人数;
中的男生人数;
(2)从 学院样本中5月份累计跑步里程不少于
学院样本中5月份累计跑步里程不少于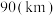 的学生中随机抽取3人,其中男生人数记为
的学生中随机抽取3人,其中男生人数记为 ,求
,求 的分布及期望.
的分布及期望.
 学院共有学生1000人,其中男生640人,女生360人.该学院体育社团为了解学生参与跑步运动的情况,按性别分层抽样,从该学院所有学生中抽取若干人作为样本,对样本中的每位学生在5月份的累计跑步里程进行统计,得到下表.
学院共有学生1000人,其中男生640人,女生360人.该学院体育社团为了解学生参与跑步运动的情况,按性别分层抽样,从该学院所有学生中抽取若干人作为样本,对样本中的每位学生在5月份的累计跑步里程进行统计,得到下表.跑步里程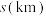 |  | 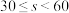 | 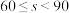 | 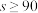 |
| 男生(人数) |  | 12 | 10 | 5 |
| 女生(人数) | 6 | 6 | 4 | 2 |
 的值,并估计
的值,并估计 学院学生5月份累计跑步里程
学院学生5月份累计跑步里程 在
在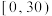 中的男生人数;
中的男生人数;(2)从
 学院样本中5月份累计跑步里程不少于
学院样本中5月份累计跑步里程不少于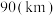 的学生中随机抽取3人,其中男生人数记为
的学生中随机抽取3人,其中男生人数记为 ,求
,求 的分布及期望.
的分布及期望.
您最近一年使用:0次
10 . 一项试验旨在研究臭氧效应.实验方案如下:选40只小白鼠,随机地将其中20只分配到实验组,另外20只分配到对照组,实验组的小白鼠饲养在高浓度臭氧环境,对照组的小白鼠饲养在正常环境,一段时间后统计每只小白鼠体重的增加量(单位:g).
(1)设 表示指定的两只小白鼠中分配到对照组的只数,求
表示指定的两只小白鼠中分配到对照组的只数,求 的分布列和数学期望;
的分布列和数学期望;
(2)实验结果如下:
对照组的小白鼠体重的增加量从小到大排序为:
15.2 18.8 20.2 21.3 22.5 23.2 25.8 26.5 27.5 30.1
32.6 34.3 34.8 35.6 35.6 35.8 36.2 37.3 40.5 43.2
实验组的小白鼠体重的增加量从小到大排序为:
7.8 9.2 11.4 12.4 13.2 15.5 16.5 18.0 18.8 19.2
19.8 20.2 21.6 22.8 23.6 23.9 25.1 28.2 32.3 36.5
(i)求40只小鼠体重的增加量的中位数m,再分别统计两样本中小于m与不小于的数据的个数,完成如下列联表:
(ii)根据(i)中的列联表,能否有95%的把握认为小白鼠在高浓度臭氧环境中与正常环境中体重的增加量有差异.
附:
(1)设
 表示指定的两只小白鼠中分配到对照组的只数,求
表示指定的两只小白鼠中分配到对照组的只数,求 的分布列和数学期望;
的分布列和数学期望;(2)实验结果如下:
对照组的小白鼠体重的增加量从小到大排序为:
15.2 18.8 20.2 21.3 22.5 23.2 25.8 26.5 27.5 30.1
32.6 34.3 34.8 35.6 35.6 35.8 36.2 37.3 40.5 43.2
实验组的小白鼠体重的增加量从小到大排序为:
7.8 9.2 11.4 12.4 13.2 15.5 16.5 18.0 18.8 19.2
19.8 20.2 21.6 22.8 23.6 23.9 25.1 28.2 32.3 36.5
(i)求40只小鼠体重的增加量的中位数m,再分别统计两样本中小于m与不小于的数据的个数,完成如下列联表:
|
| |
对照组 | ||
实验组 |
附:

| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
2023-06-09更新
|
21682次组卷
|
30卷引用:上海市奉贤区奉贤中学2024届高三下学期开学考试数学试题
上海市奉贤区奉贤中学2024届高三下学期开学考试数学试题2023年高考全国甲卷数学(理)真题全国甲乙卷真题5年分类汇编《概率统计》解答题全国甲乙卷3年真题分类汇编《概率统计》解答题专题08计数原理与概率统计(成品)(已下线)2023年高考全国甲卷数学(理)真题变式题16-20福建省晋江市平山学校、泉州中远学校、晋江市内坑中学、晋江市磁灶中学、永春第二中学2022-2023学年高二下学期期末联考数学试题(已下线)专题09 计数原理与概率统计-1(已下线)第07讲 离散型随机变量的分布列与数字特征(练习)河北省唐山市开滦第一中学2024届高三上学期12月月考数学试题(已下线)考点17 列联表与独立性检验 2024届高考数学考点总动员云南、黑龙江、陕西、河南四省2024届高中毕业生联合命题数学试卷(一)(已下线)第七章 统计案例(单元综合检测卷)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)河南省信阳市浉河区信阳高级中学2024届高三上学期1月月考数学试题(已下线)专题11 统计与概率(解密讲义)(已下线)专题08 统计案例分析(讲义)(已下线)题型27 5类概率统计大题综合解题技巧(已下线)【一题多变】 分类变量 独立检验(已下线)专题10.1 概率与统计的综合运用【十一大题型】(举一反三)(新高考专用)-2(已下线)专题25 概率统计解答题(理科)-3(已下线)专题4 考前押题大猜想16-20【人教A版(2019)】专题14概率与统计(第四部分)-高二下学期名校期末好题汇编专题09统计与成对数据的统计分析专题33概率统计解答题(第二部分)(已下线)三年全国理科专题09计数原理与概率统计(已下线)五年全国理科专题11概率统计选择填空题(已下线)作业03 概率(2)-【暑假分层作业】(苏教版2019选择性必修第二册)【巩固卷】第4章 统计 高考强化 单元测试B-湘教版(2019)选择性必修第二册(已下线)二项分布与超几何分布、正态分布-一轮复习考点专练(已下线)第五章 概率统计创新问题 专题一 概率统计决策问题 微点2 概率统计决策问题(二)【基础版】