1 . 某物流公司专营从甲地到乙地的货运业务,现统计了最近400天内每天可配送的货物量,按照可配送货物量 (单位:箱)分成了以下几组:
(单位:箱)分成了以下几组: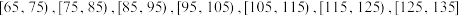 ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图. (单位:箱)服从
(单位:箱)服从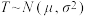 的正态分布,经计算
的正态分布,经计算 近似为
近似为 近似为150.
近似为150.
①利用该正态分布.求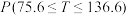 ;
;
②试利用该正态分布,估计该物流公司2000天内货物配送量在区间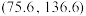 内的天数(结果保留整数).
内的天数(结果保留整数).
(2)该物流公司负责人根据每日的可配送货物量为装卸员工制定了两种不同的工作奖励方案.
方案一:利用该频率分布直方图获取相关概率(将图中的频率视为概率),采用直接发放奖金的方式奖励员工,按每日的可配送货物量划分为三级: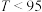 时,奖励60元;
时,奖励60元;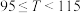 时,奖励80元;
时,奖励80元;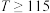 时,奖励120元;方案二:利用正态分布获取相关概率,采用抽奖的方式奖励员工,其中每日的可配送货物量不低于
时,奖励120元;方案二:利用正态分布获取相关概率,采用抽奖的方式奖励员工,其中每日的可配送货物量不低于 时有两次抽奖机会,每日的可配送货物量低于
时有两次抽奖机会,每日的可配送货物量低于 时只有一次抽奖机会,每次抽奖的奖金及对应的概率如下表:
时只有一次抽奖机会,每次抽奖的奖金及对应的概率如下表:
小张为该公司装卸货物的一名员工,试从员工所得奖金的数学期望角度分析,小张选择哪种奖励方案对他更有利?
附: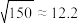 ,若
,若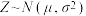 ,则
,则

 (单位:箱)分成了以下几组:
(单位:箱)分成了以下几组: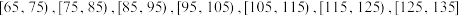 ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.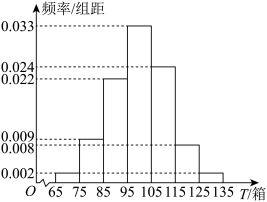
 (单位:箱)服从
(单位:箱)服从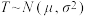 的正态分布,经计算
的正态分布,经计算 近似为
近似为 近似为150.
近似为150.①利用该正态分布.求
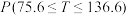 ;
;②试利用该正态分布,估计该物流公司2000天内货物配送量在区间
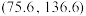 内的天数(结果保留整数).
内的天数(结果保留整数).(2)该物流公司负责人根据每日的可配送货物量为装卸员工制定了两种不同的工作奖励方案.
方案一:利用该频率分布直方图获取相关概率(将图中的频率视为概率),采用直接发放奖金的方式奖励员工,按每日的可配送货物量划分为三级:
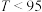 时,奖励60元;
时,奖励60元;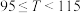 时,奖励80元;
时,奖励80元;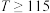 时,奖励120元;方案二:利用正态分布获取相关概率,采用抽奖的方式奖励员工,其中每日的可配送货物量不低于
时,奖励120元;方案二:利用正态分布获取相关概率,采用抽奖的方式奖励员工,其中每日的可配送货物量不低于 时有两次抽奖机会,每日的可配送货物量低于
时有两次抽奖机会,每日的可配送货物量低于 时只有一次抽奖机会,每次抽奖的奖金及对应的概率如下表:
时只有一次抽奖机会,每次抽奖的奖金及对应的概率如下表:资金 | 50 | 100 |
概率 |
|
|
附:
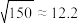 ,若
,若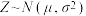 ,则
,则
您最近一年使用:0次
23-24高二上·山东德州·期末
解题方法
2 . 某物流公司专营从甲地到乙地的货运业务,现统计了最近500天内每天可配送的货物量,按照可配送货物量T(单位:箱)分成了以下几组: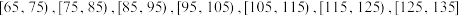 ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.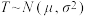 的正态分布,经计算
的正态分布,经计算 近似为
近似为 近似为150.
近似为150.
①利用该正态分布,求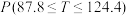 ;
;
②试利用该正态分布,估计该物流公司2000天内货物配送量在区间(87.8,124.4)内的天数(结果保留整数).
(2)该物流公司负责人根据每日的可配送货物量为装卸员工制定了两种不同的工作奖励方案.
方案一:利用该频率分布直方图获取相关概率(将图中的频率视为概率),采用直接发放奖金的方式奖励员工,按每日的可配送货物量划分为三级: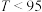 时,奖励50元;
时,奖励50元;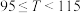 时,奖励80元;
时,奖励80元;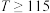 时,奖励120元;方案二:利用正态分布获取相关概率,采用抽奖的方式奖励员工,其中每日的可配送货物量不低于
时,奖励120元;方案二:利用正态分布获取相关概率,采用抽奖的方式奖励员工,其中每日的可配送货物量不低于 时有两次抽奖机会,每日的可配送货物量低于
时有两次抽奖机会,每日的可配送货物量低于 时只有一次抽奖机会,每次抽奖的奖金及对应的概率如下表:
时只有一次抽奖机会,每次抽奖的奖金及对应的概率如下表:
小张为该公司装卸货物的一名员工,试从员工所得奖金的数学期望角度分析,小张选择哪种奖励方案对他更有利?
附: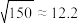 ,若
,若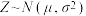 ,则
,则 .
.
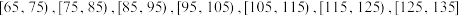 ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.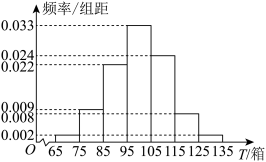
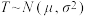 的正态分布,经计算
的正态分布,经计算 近似为
近似为 近似为150.
近似为150.①利用该正态分布,求
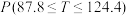 ;
;②试利用该正态分布,估计该物流公司2000天内货物配送量在区间(87.8,124.4)内的天数(结果保留整数).
(2)该物流公司负责人根据每日的可配送货物量为装卸员工制定了两种不同的工作奖励方案.
方案一:利用该频率分布直方图获取相关概率(将图中的频率视为概率),采用直接发放奖金的方式奖励员工,按每日的可配送货物量划分为三级:
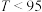 时,奖励50元;
时,奖励50元;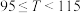 时,奖励80元;
时,奖励80元;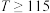 时,奖励120元;方案二:利用正态分布获取相关概率,采用抽奖的方式奖励员工,其中每日的可配送货物量不低于
时,奖励120元;方案二:利用正态分布获取相关概率,采用抽奖的方式奖励员工,其中每日的可配送货物量不低于 时有两次抽奖机会,每日的可配送货物量低于
时有两次抽奖机会,每日的可配送货物量低于 时只有一次抽奖机会,每次抽奖的奖金及对应的概率如下表:
时只有一次抽奖机会,每次抽奖的奖金及对应的概率如下表:奖金 | 50 | 100 |
概率 |
|
|
附:
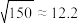 ,若
,若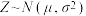 ,则
,则 .
.
您最近一年使用:0次
名校
3 . 某公司在一次年终总结会上举行抽奖活动,在一个不透明的箱子中放入3个红球和3个白球(球的形状和大小都相同),抽奖规则有以下两种方案可供选择:
方案一:选取一名员工在袋中随机摸出一个球,若是红球,则放回袋中;若是白球,则不放回,再在袋中补充一个红球,这样反复进行3次,若最后袋中红球个数为 ,则每位员工颁发奖金
,则每位员工颁发奖金 万元;
万元;
方案二:从袋中一次性摸出3个球,把白球换成红球再全部放回袋中,设袋中红球个数为 ,则每位员工颁发奖金
,则每位员工颁发奖金 万元.
万元.
(1)若用方案一,求 的分布列与数学期望;
的分布列与数学期望;
(2)比较方案一与方案二,求采用哪种方案,员工获得奖金数额的数学期望值更高?请说明理由;
(3)若企业有1000名员工,他们为企业贡献的利润近似服从正态分布 ,
, 为各位员工贡献利润数额的均值,计算结果为100万元,
为各位员工贡献利润数额的均值,计算结果为100万元, 为数据的方差,计算结果为225万元,若规定奖金只有贡献利润大于115万元的员工可以获得,若按方案一与方案二两种抽奖方式获得奖金的数学期望值的最大值计算,求获奖员工的人数及每人可以获得奖金的平均数值(保留到整数)参考数据:若随机变量
为数据的方差,计算结果为225万元,若规定奖金只有贡献利润大于115万元的员工可以获得,若按方案一与方案二两种抽奖方式获得奖金的数学期望值的最大值计算,求获奖员工的人数及每人可以获得奖金的平均数值(保留到整数)参考数据:若随机变量 服从正态分布
服从正态分布 ,则
,则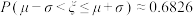
方案一:选取一名员工在袋中随机摸出一个球,若是红球,则放回袋中;若是白球,则不放回,再在袋中补充一个红球,这样反复进行3次,若最后袋中红球个数为
 ,则每位员工颁发奖金
,则每位员工颁发奖金 万元;
万元;方案二:从袋中一次性摸出3个球,把白球换成红球再全部放回袋中,设袋中红球个数为
 ,则每位员工颁发奖金
,则每位员工颁发奖金 万元.
万元.(1)若用方案一,求
 的分布列与数学期望;
的分布列与数学期望;(2)比较方案一与方案二,求采用哪种方案,员工获得奖金数额的数学期望值更高?请说明理由;
(3)若企业有1000名员工,他们为企业贡献的利润近似服从正态分布
 ,
, 为各位员工贡献利润数额的均值,计算结果为100万元,
为各位员工贡献利润数额的均值,计算结果为100万元, 为数据的方差,计算结果为225万元,若规定奖金只有贡献利润大于115万元的员工可以获得,若按方案一与方案二两种抽奖方式获得奖金的数学期望值的最大值计算,求获奖员工的人数及每人可以获得奖金的平均数值(保留到整数)参考数据:若随机变量
为数据的方差,计算结果为225万元,若规定奖金只有贡献利润大于115万元的员工可以获得,若按方案一与方案二两种抽奖方式获得奖金的数学期望值的最大值计算,求获奖员工的人数及每人可以获得奖金的平均数值(保留到整数)参考数据:若随机变量 服从正态分布
服从正态分布 ,则
,则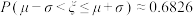
您最近一年使用:0次
2023-04-22更新
|
1136次组卷
|
9卷引用:第七章 随机变量及其分布(单元测试)
(已下线)第七章 随机变量及其分布(单元测试)江西省南昌市铁路第一中学2022-2023学年高二下学期第二次月考数学试题上海市松江二中2023-2024学年高二下学期5月考数学试卷(已下线)核心考点7 二项分布与超几何分布、正态分布 B提升卷 (高二期末考试必考的10大核心考点)(已下线)高二下学期第二次月考模拟试题01(数列、圆锥曲线、导数、排列组合、概率、随机变量及其分布)山西省名校2022-2023学年高二下学期7月期末联合测评数学试题浙江省A9协作体2022-2023学年高二下学期期中联考数学试题湖北省郧阳中学、恩施高中、随州二中、襄阳三中2022-2023学年高二下学期五月联考数学试题江西省宁冈中学2022-2023学年高二下学期6月期末数学试题
4 . 《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为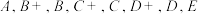 共8个等级.参照正态分布原则,确定各等级人数所占比例分别为
共8个等级.参照正态分布原则,确定各等级人数所占比例分别为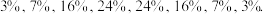 选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100],[81,90],[71,80],[61,70],[51,60],[41,50],[31,40],[21,30]八个分数区间,得到考生的等级成绩.某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布
选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100],[81,90],[71,80],[61,70],[51,60],[41,50],[31,40],[21,30]八个分数区间,得到考生的等级成绩.某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布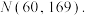
(1)求物理原始成绩在区间[47,86]的人数;
(2)按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间[61,80]的人数,求X的分布列和数学期望.
(附:若随机变量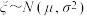 ,则
,则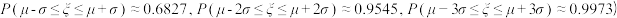
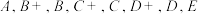 共8个等级.参照正态分布原则,确定各等级人数所占比例分别为
共8个等级.参照正态分布原则,确定各等级人数所占比例分别为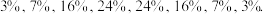 选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100],[81,90],[71,80],[61,70],[51,60],[41,50],[31,40],[21,30]八个分数区间,得到考生的等级成绩.某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布
选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100],[81,90],[71,80],[61,70],[51,60],[41,50],[31,40],[21,30]八个分数区间,得到考生的等级成绩.某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布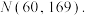
(1)求物理原始成绩在区间[47,86]的人数;
(2)按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间[61,80]的人数,求X的分布列和数学期望.
(附:若随机变量
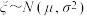 ,则
,则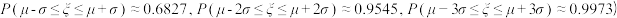
您最近一年使用:0次
名校
5 . 甲企业生产线上生产的零件尺寸的误差 服从正态分布
服从正态分布 ,规定
,规定 的零件为优等品,
的零件为优等品, 的零件为合格品.
的零件为合格品.
(1)从该生产线上随机抽取100个零件,估计抽到合格品但非优等品的个数(精确到整数);
(2)乙企业拟向甲企业购买这批零件,先对该批零件进行质量抽检,检测的方案是:从这批零件中任取2个作检测,若这2个零件都是优等品,则通过检测;若这2个零件中恰有1个为优等品,1个为合格品但非优等品,则再从这批零件中任取1个作检测,若为优等品,则通过检测;其余情况都不通过检测.求这批零件通过检测时,检测了2个零件的概率(精确到0.01).
(附:若随机变量 ,则
,则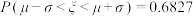 ,
,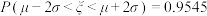 ,
,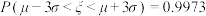 )
)
 服从正态分布
服从正态分布 ,规定
,规定 的零件为优等品,
的零件为优等品, 的零件为合格品.
的零件为合格品.(1)从该生产线上随机抽取100个零件,估计抽到合格品但非优等品的个数(精确到整数);
(2)乙企业拟向甲企业购买这批零件,先对该批零件进行质量抽检,检测的方案是:从这批零件中任取2个作检测,若这2个零件都是优等品,则通过检测;若这2个零件中恰有1个为优等品,1个为合格品但非优等品,则再从这批零件中任取1个作检测,若为优等品,则通过检测;其余情况都不通过检测.求这批零件通过检测时,检测了2个零件的概率(精确到0.01).
(附:若随机变量
 ,则
,则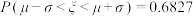 ,
,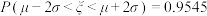 ,
,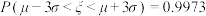 )
)
您最近一年使用:0次
2024-05-07更新
|
1386次组卷
|
5卷引用:福建省福州市2023-2024学年高三下学期4月末质量检测数学试卷
福建省福州市2023-2024学年高三下学期4月末质量检测数学试卷(已下线)专题2 科学研究情境河北省邢台市南宫中学2023-2024学年高三高考考前定心卷3数学试题(已下线)二项分布与超几何分布、正态分布-一轮复习考点专练(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(练习)-1
名校
解题方法
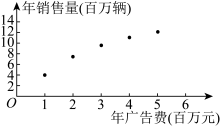
6 . 台州是全国三大电动车生产基地之一,拥有完整的产业链和突出的设计优势.某电动车公司为了抢占更多的市场份额,计划加大广告投入、该公司近5年的年广告费 (单位:百万元)和年销售量
(单位:百万元)和年销售量 (单位:百万辆)关系如图所示:令
(单位:百万辆)关系如图所示:令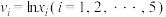 ,数据经过初步处理得:
,数据经过初步处理得:
现有①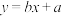 和②
和② 两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,b,m,n均为常数.
两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,b,m,n均为常数.
(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)根据(1)的分析选取拟合程度更好的回归分析模型及表中数据,求出y关于x的回归方程,并预测年广告费为6(百万元)时,产品的年销售量是多少?
(3)该公司生产的电动车毛利润为每辆200元(不含广告费、研发经费).该公司在加大广告投入的同时也加大研发经费的投入,年研发经费为年广告费的199倍.电动车的年净利润受年广告费和年研发经费影响外还受随机变量 影响,设随机变量
影响,设随机变量 服从正态分布
服从正态分布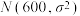 ,且满足
,且满足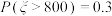 .在(2)的条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量).
.在(2)的条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量).
附:①相关系数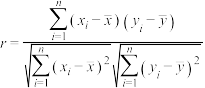 ,
,
回归直线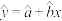 中公式分别为
中公式分别为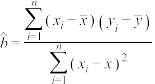 ,
, ;
;
②参考数据: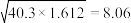 ,
,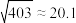 ,
, ,
, .
.
 (单位:百万元)和年销售量
(单位:百万元)和年销售量 (单位:百万辆)关系如图所示:令
(单位:百万辆)关系如图所示:令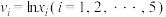 ,数据经过初步处理得:
,数据经过初步处理得:
 | 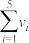 | 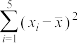 | 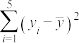 | 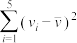 |  |  |
| 44 | 4.8 | 10 | 40.3 | 1.612 | 19.5 | 8.06 |
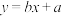 和②
和② 两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,b,m,n均为常数.
两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,b,m,n均为常数.(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)根据(1)的分析选取拟合程度更好的回归分析模型及表中数据,求出y关于x的回归方程,并预测年广告费为6(百万元)时,产品的年销售量是多少?
(3)该公司生产的电动车毛利润为每辆200元(不含广告费、研发经费).该公司在加大广告投入的同时也加大研发经费的投入,年研发经费为年广告费的199倍.电动车的年净利润受年广告费和年研发经费影响外还受随机变量
 影响,设随机变量
影响,设随机变量 服从正态分布
服从正态分布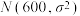 ,且满足
,且满足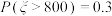 .在(2)的条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量).
.在(2)的条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量).附:①相关系数
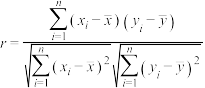 ,
,回归直线
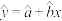 中公式分别为
中公式分别为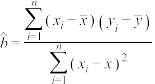 ,
, ;
;②参考数据:
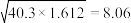 ,
,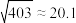 ,
, ,
, .
.
您最近一年使用:0次
2024-04-18更新
|
3756次组卷
|
11卷引用:浙江省台州市2024届高三下学期第二次教学质量评估数学试题
浙江省台州市2024届高三下学期第二次教学质量评估数学试题(已下线)第八章 成对数据的统计分析总结 第一练 考点强化训练(已下线)模块二 专题1统计案例中决策分析问题(北师大高二)(已下线)8.5 二项分布、超几何分布与正态分布(高考真题素材之十年高考)山西省太原市第五中学2023-2024学年高二下学期5月月考数学试题(已下线)专题04 第八章 成对数据的统计分析--高二期末考点大串讲(人教A版2019)(已下线)第八章 成对数据的统计分析(基础卷)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)湖北省武汉市黄陂区第七高级中学2024届高三模拟考试(二)数学试题(已下线)第四章 统计 专题四 相关分析与回归分析 微点3 相关分析与回归分析(三)【基础版】湖北省襄阳市第五中学2024届高三下学期第四次适应性测试数学试题云南省大理新世纪中学2024届高三数学模拟试题
名校
7 . 某市举行了一次大型宣传活动,会后组办方分别从7个不同的地方的问卷调查中各随机抽取了相同数量的数据构成一个样本,依据相关的标准该样本中各地抽取的数据人均得分构成数列 ,且
,且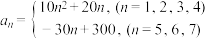 ,由各地的得分可以认为各地人均得分2服从正态分布
,由各地的得分可以认为各地人均得分2服从正态分布 ,
, 近似为抽取的样本中7个地方人均得分的平均值(得分的平均值四舍五入并取整数).
近似为抽取的样本中7个地方人均得分的平均值(得分的平均值四舍五入并取整数).
(1)利用正态分布的知识求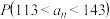 ;
;
(2)组办方为此次参加问卷调查的市民制定如下两种奖励方案:
方案一:(i)得分不低于 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ii)每次获赠的随机话费和对应的概率为
方案二:参加了此次问卷调查的市民可获得价值100元的“元旦迎新”大型晚会活动入场券,参加了此次问卷调查的市民可选择其中一种奖励方案.
①市民小李参加了此次问卷调查,记X(单位:元)为小李参加问卷调查获赠的话费,求X的分布列及数学期望;
②请问小李是选择参加获赠随机话费活动,还是获得价值100元的参加“元旦迎新”入场券?请用统计中相关知识为小李作出决策.
(附:若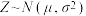 ,则
,则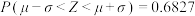 ,
,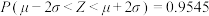 ,
,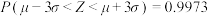 )
)
 ,且
,且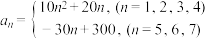 ,由各地的得分可以认为各地人均得分2服从正态分布
,由各地的得分可以认为各地人均得分2服从正态分布 ,
, 近似为抽取的样本中7个地方人均得分的平均值(得分的平均值四舍五入并取整数).
近似为抽取的样本中7个地方人均得分的平均值(得分的平均值四舍五入并取整数).(1)利用正态分布的知识求
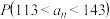 ;
;(2)组办方为此次参加问卷调查的市民制定如下两种奖励方案:
方案一:(i)得分不低于
 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于 的可以获赠1次随机话费;
的可以获赠1次随机话费;(ii)每次获赠的随机话费和对应的概率为
获赠的随机话费(单位:元) | 50 | 100 |
概率 |
|
|
①市民小李参加了此次问卷调查,记X(单位:元)为小李参加问卷调查获赠的话费,求X的分布列及数学期望;
②请问小李是选择参加获赠随机话费活动,还是获得价值100元的参加“元旦迎新”入场券?请用统计中相关知识为小李作出决策.
(附:若
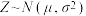 ,则
,则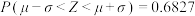 ,
,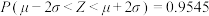 ,
,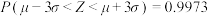 )
)
您最近一年使用:0次
8 . 某小区开展了两会知识问答活动,现将该小区参与该活动的240位居民的得分(满分100分)进行了统计,得到如下的频率分布直方图.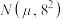 ,其中
,其中 近似为参与本次活动的240位居民的平均得分(同一组中的数据用该组区间的中点值代表),求
近似为参与本次活动的240位居民的平均得分(同一组中的数据用该组区间的中点值代表),求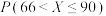 的值;
的值;
(2)本次活动,制定了如下奖励方案:参与本次活动得分低于 的居民获得一次抽奖机会,参与本次活动得分不低于
的居民获得一次抽奖机会,参与本次活动得分不低于 的居民获得两次抽奖机会,每位居民每次有
的居民获得两次抽奖机会,每位居民每次有 的机会抽中一张10元的话费充值卡,有
的机会抽中一张10元的话费充值卡,有 的机会抽中一张20元的话费充值卡,假设每次抽奖相互独立,假设该小区居民王先生参与本次活动,求王先生获得的话费充值卡的总金额Y的概率分布列,并估计本次活动需要准备的话费充值卡的总金额.
的机会抽中一张20元的话费充值卡,假设每次抽奖相互独立,假设该小区居民王先生参与本次活动,求王先生获得的话费充值卡的总金额Y的概率分布列,并估计本次活动需要准备的话费充值卡的总金额.
参考数据: ,
,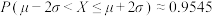 ,
, .
.

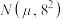 ,其中
,其中 近似为参与本次活动的240位居民的平均得分(同一组中的数据用该组区间的中点值代表),求
近似为参与本次活动的240位居民的平均得分(同一组中的数据用该组区间的中点值代表),求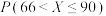 的值;
的值;(2)本次活动,制定了如下奖励方案:参与本次活动得分低于
 的居民获得一次抽奖机会,参与本次活动得分不低于
的居民获得一次抽奖机会,参与本次活动得分不低于 的居民获得两次抽奖机会,每位居民每次有
的居民获得两次抽奖机会,每位居民每次有 的机会抽中一张10元的话费充值卡,有
的机会抽中一张10元的话费充值卡,有 的机会抽中一张20元的话费充值卡,假设每次抽奖相互独立,假设该小区居民王先生参与本次活动,求王先生获得的话费充值卡的总金额Y的概率分布列,并估计本次活动需要准备的话费充值卡的总金额.
的机会抽中一张20元的话费充值卡,假设每次抽奖相互独立,假设该小区居民王先生参与本次活动,求王先生获得的话费充值卡的总金额Y的概率分布列,并估计本次活动需要准备的话费充值卡的总金额.参考数据:
 ,
,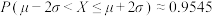 ,
, .
.
您最近一年使用:0次
2024-06-20更新
|
370次组卷
|
3卷引用:【高二模块二】类型3 以随机变量及其分布为背景的解答题(A卷基础卷)
(已下线)【高二模块二】类型3 以随机变量及其分布为背景的解答题(A卷基础卷)内蒙古自治区赤峰市敖汉旗箭桥中学2025届高三上学期开学考试数学试卷湖南省邵阳市邵东市第四中学2023-2024学年高二下学期4月期中考试数学试题
名校
9 . 某公司为考核员工,采用某方案对员工进行业务技能测试,并统计分析测试成绩以确定员工绩效等级.
(1)已知该公司甲部门有3名负责人,乙部门有4名负责人,该公司从甲、乙两部门中随机选取3名负责人做测试分析,记负责人来自甲部门的人数为 ,求
,求 的最有可能的取值:
的最有可能的取值:
(2)该公司统计了七个部门测试的平均成绩 (满分100分)与绩效等级优秀率
(满分100分)与绩效等级优秀率 ,如下表所示:
,如下表所示:
根据数据绘制散点图,初步判断,选用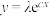 作为回归方程.令
作为回归方程.令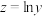 ,经计算得
,经计算得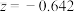 ,
,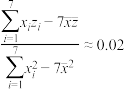
(ⅰ)已知某部门测试的平均成绩为60分,估计其绩效等级优秀率;
(ⅱ)根据统计分析,大致认为各部门测试平均成绩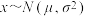 ,其中
,其中 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .经计算
.经计算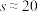 ,求某个部门绩效等级优秀率不低于
,求某个部门绩效等级优秀率不低于 的概率.
的概率.
参考公式与数据:①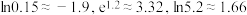 .
.
②线性回归方程 中,
中, ,
, .
.
③若随机变量 ,则
,则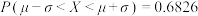 ,
, ,
, .
.
(1)已知该公司甲部门有3名负责人,乙部门有4名负责人,该公司从甲、乙两部门中随机选取3名负责人做测试分析,记负责人来自甲部门的人数为
 ,求
,求 的最有可能的取值:
的最有可能的取值:(2)该公司统计了七个部门测试的平均成绩
 (满分100分)与绩效等级优秀率
(满分100分)与绩效等级优秀率 ,如下表所示:
,如下表所示: | 32 | 41 | 54 | 68 | 74 | 80 | 92 |
 | 0.28 | 0.34 | 0.44 | 0.58 | 0.66 | 0.74 | 0.94 |
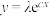 作为回归方程.令
作为回归方程.令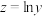 ,经计算得
,经计算得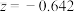 ,
,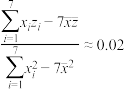
(ⅰ)已知某部门测试的平均成绩为60分,估计其绩效等级优秀率;
(ⅱ)根据统计分析,大致认为各部门测试平均成绩
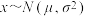 ,其中
,其中 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .经计算
.经计算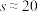 ,求某个部门绩效等级优秀率不低于
,求某个部门绩效等级优秀率不低于 的概率.
的概率.参考公式与数据:①
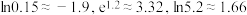 .
.②线性回归方程
 中,
中, ,
, .
.③若随机变量
 ,则
,则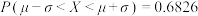 ,
, ,
, .
.
您最近一年使用:0次
2024-05-14更新
|
2845次组卷
|
6卷引用:山东省日照市2024届高三下学期校际联考(二模)数学试题
山东省日照市2024届高三下学期校际联考(二模)数学试题河南省信阳市新县高级中学2024届高三考前第六次适应性考试数学试题安徽省六安市霍山文峰学校2024届高三最后一卷数学试卷(已下线)模型4 以超几何分布为背景的离散型随机变量问题模型(第9章 计数原理、概率、随机变量及其分布 )河南省信阳市新县高级中学2025届高三上学期适应性考试(一)数学试题(已下线)第四章 统计 专题四 相关分析与回归分析 微点3 相关分析与回归分析(三)【基础版】
名校
10 . 某省2023年开始将全面实施新高考方案.在6门选择性考试科目中,物理、历史这两门科目采用原始分计分:思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为A、B,C,D,E共5个等级,各等级人数所占比例分别为15%、35%、35%、13%和2%,并按给定的公式进行转换赋分.该省部分学校联合组织了一次高二年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.
(1)其中一所学校某班生物学科获得A等级的共有10名学生,其原始分及转换赋分如表:
现从这10名学生中随机抽取3人,设这3人中生物的赋分不低于95分的人数为X,求X的分布列和数学期望:
(2)假设此次高二学生生物学科原始分Y近似服从正态分布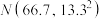 .现随机抽取了100名高二学生的此次生物学科的原始分,后经调查发现其中有一名学生舞弊,剔除掉这名学生成绩后,记ξ为其他被抽到的原始分不低于80分的学生人数,预测当
.现随机抽取了100名高二学生的此次生物学科的原始分,后经调查发现其中有一名学生舞弊,剔除掉这名学生成绩后,记ξ为其他被抽到的原始分不低于80分的学生人数,预测当 取得最大值时k的值.
取得最大值时k的值.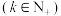
附,若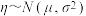 ,则
,则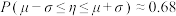 ,
,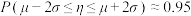 .
.
(1)其中一所学校某班生物学科获得A等级的共有10名学生,其原始分及转换赋分如表:
| 原始分 | 97 | 95 | 91 | 90 | 89 | 87 | 85 | 84 | 84 | 83 |
| 赋分 | 99 | 97 | 95 | 95 | 94 | 92 | 91 | 90 | 90 | 90 |
(2)假设此次高二学生生物学科原始分Y近似服从正态分布
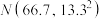 .现随机抽取了100名高二学生的此次生物学科的原始分,后经调查发现其中有一名学生舞弊,剔除掉这名学生成绩后,记ξ为其他被抽到的原始分不低于80分的学生人数,预测当
.现随机抽取了100名高二学生的此次生物学科的原始分,后经调查发现其中有一名学生舞弊,剔除掉这名学生成绩后,记ξ为其他被抽到的原始分不低于80分的学生人数,预测当 取得最大值时k的值.
取得最大值时k的值.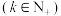
附,若
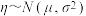 ,则
,则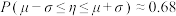 ,
,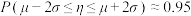 .
.
您最近一年使用:0次
2024-04-30更新
|
1000次组卷
|
9卷引用:7.5 正态分布(6大题型)精讲-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)
(已下线)7.5 正态分布(6大题型)精讲-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)高二期末模拟卷01(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)(已下线)第五章 概率统计创新问题 专题三 概率统计中的函数思想 微点3 概率统计中的函数思想综合训练【基础版】江西省景德镇市一中2023-2024学年高二下学期4月期中考试数学试题(已下线)专题06 离散型随机变量分布列及正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)(已下线)专题06 离散型随机变量与正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)山东省济宁市第一中学2023-2024学年高二下学期质量检测(三)(6月)数学试题广东省深圳市人大附中深圳学校2023-2024学年高二下学期期中考试数学试卷







