名校
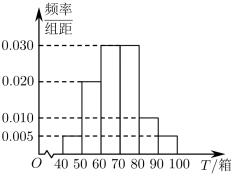
1 . 某物流公司专营从甲地到乙地的货运业务(货物全部用统一规格的包装箱包装),现统计了最近100天内每天可配送的货物量,按照可配送的货物量 (单位:箱)分成了以下几组:
(单位:箱)分成了以下几组: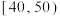 ,
, ,
, ,
, ,
, ,
, ,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
(1)该物流公司负责人决定用分层抽样的方法从前3组中随机抽出11天的数据来分析每日的可配送货物量少的原因,并从这11天的数据中再抽出3天的数据进行财务分析,求这3天的数据中至少有2天的数据来自 这一组的概率;
这一组的概率;
(2)该物流公司负责人根据每日的可配送货物量为公司装卸货物的员工制定了两种不同的工作奖励方案.
方案一:直接发放奖金,按每日的可配送货物量划分为三级,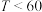 时,奖励50元;
时,奖励50元;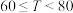 时,奖励80元;
时,奖励80元; 时,奖励120元.
时,奖励120元.
方案二:利用抽奖的方式获得奖金,其中每日的可配送货物量不低于样本的中位数时有两次抽奖机会,每日的可配送货物量低于样本的中位数时只有一次抽奖机会,每次抽奖的奖金及对应的概率为
小张为该公司装卸货物的一名员工,试从数学期望的角度分析,小张选择哪种奖励方案对他更有利?
(3)由频率分布直方图可以认为,该物流公司每日的可配送货物量 (单位:箱)近似服从正态分布
(单位:箱)近似服从正态分布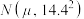 ,其中
,其中 近似为样本平均数.试利用该正态分布,估计该物流公司2000天内日货物配送量在区间
近似为样本平均数.试利用该正态分布,估计该物流公司2000天内日货物配送量在区间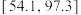 内的天数(结果保留整数).
内的天数(结果保留整数).
附:若 ,则
,则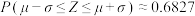 ,
,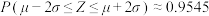 .
.
 (单位:箱)分成了以下几组:
(单位:箱)分成了以下几组: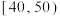 ,
, ,
, ,
, ,
, ,
, ,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
(1)该物流公司负责人决定用分层抽样的方法从前3组中随机抽出11天的数据来分析每日的可配送货物量少的原因,并从这11天的数据中再抽出3天的数据进行财务分析,求这3天的数据中至少有2天的数据来自
 这一组的概率;
这一组的概率;(2)该物流公司负责人根据每日的可配送货物量为公司装卸货物的员工制定了两种不同的工作奖励方案.
方案一:直接发放奖金,按每日的可配送货物量划分为三级,
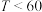 时,奖励50元;
时,奖励50元;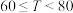 时,奖励80元;
时,奖励80元; 时,奖励120元.
时,奖励120元.方案二:利用抽奖的方式获得奖金,其中每日的可配送货物量不低于样本的中位数时有两次抽奖机会,每日的可配送货物量低于样本的中位数时只有一次抽奖机会,每次抽奖的奖金及对应的概率为
| 奖金 | 50 | 100 |
| 概率 |  |  |
(3)由频率分布直方图可以认为,该物流公司每日的可配送货物量
 (单位:箱)近似服从正态分布
(单位:箱)近似服从正态分布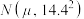 ,其中
,其中 近似为样本平均数.试利用该正态分布,估计该物流公司2000天内日货物配送量在区间
近似为样本平均数.试利用该正态分布,估计该物流公司2000天内日货物配送量在区间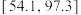 内的天数(结果保留整数).
内的天数(结果保留整数).附:若
 ,则
,则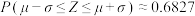 ,
,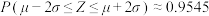 .
.
您最近一年使用:0次
2023-05-21更新
|
783次组卷
|
2卷引用:福建省泉州第五中学2023届高三毕业班高考适应性检测(一)数学试题
名校
2 . 零部件生产水平是评判一个国家高端装备制造能力的重要标准之一,其中切割加工技术是一项重要技术.某精密仪器制造商研发了一种切割设备,用来生产高精度的机械零件,经过长期生产检验,可以认为该设备生产的零件尺寸服从正态分布 .某机械加工厂购买了该切割设备,在正式投入生产前进行了试生产,从试生产的零件中任意抽取10件作为样本,下面是样本的尺寸
.某机械加工厂购买了该切割设备,在正式投入生产前进行了试生产,从试生产的零件中任意抽取10件作为样本,下面是样本的尺寸 (
(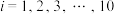 ,单位:
,单位: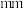 ):
):
用样本的平均数 作为
作为 的估计值,用样本的标准差
的估计值,用样本的标准差 作为
作为 的估计值.
的估计值.
(1)按照技术标准的要求,若样本尺寸均在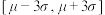 范围内,则认定该设备质量合格,根据数据判断该切割设备的质量是否合格;
范围内,则认定该设备质量合格,根据数据判断该切割设备的质量是否合格;
(2)该机械加工厂将该切割设备投入生产,对生产的零件制订了两种销售方案(假设每种方案对销售量没有影响):
方案1:每个零件均按70元定价销售;
方案2:若零件的实际尺寸在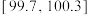 范围内,则该零件为
范围内,则该零件为 级零件,每个零件定价100元,否则为
级零件,每个零件定价100元,否则为 级零件,每个零件定价60元.
级零件,每个零件定价60元.
哪种销售方案的利润更大?请根据数据计算说明.
附: ,样本方差
,样本方差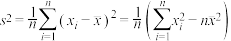 .
.
 .某机械加工厂购买了该切割设备,在正式投入生产前进行了试生产,从试生产的零件中任意抽取10件作为样本,下面是样本的尺寸
.某机械加工厂购买了该切割设备,在正式投入生产前进行了试生产,从试生产的零件中任意抽取10件作为样本,下面是样本的尺寸 (
(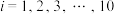 ,单位:
,单位: ):
):100.03 | 100.4 | 99.92 | 100.52 | 99.98 |
100.35 | 99.92 | 100.44 | 100.66 | 100.78 |
 作为
作为 的估计值,用样本的标准差
的估计值,用样本的标准差 作为
作为 的估计值.
的估计值.(1)按照技术标准的要求,若样本尺寸均在
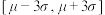 范围内,则认定该设备质量合格,根据数据判断该切割设备的质量是否合格;
范围内,则认定该设备质量合格,根据数据判断该切割设备的质量是否合格;(2)该机械加工厂将该切割设备投入生产,对生产的零件制订了两种销售方案(假设每种方案对销售量没有影响):
方案1:每个零件均按70元定价销售;
方案2:若零件的实际尺寸在
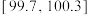 范围内,则该零件为
范围内,则该零件为 级零件,每个零件定价100元,否则为
级零件,每个零件定价100元,否则为 级零件,每个零件定价60元.
级零件,每个零件定价60元.哪种销售方案的利润更大?请根据数据计算说明.
附:
 ,样本方差
,样本方差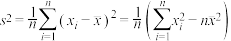 .
.
您最近一年使用:0次
2021-09-23更新
|
529次组卷
|
7卷引用:福建省泉州第五中学2020-2021学年高二下学期期末数学试题
名校
3 . 下列说法中正确的是( )
①设随机变量 服从二项分布
服从二项分布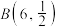 ,则
,则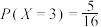
②已知随机变量 服从正态分布
服从正态分布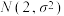 且
且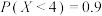 ,则
,则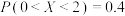
③2023年7月28日第31届成都大学生运动会在成都隆重开幕,将5名大运会志愿者分配到游泳、乒乓球、篮球和排球4个项目进行志愿者服务,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有180种;
④ ,
,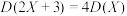 .
.
①设随机变量
 服从二项分布
服从二项分布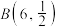 ,则
,则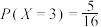
②已知随机变量
 服从正态分布
服从正态分布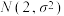 且
且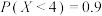 ,则
,则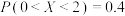
③2023年7月28日第31届成都大学生运动会在成都隆重开幕,将5名大运会志愿者分配到游泳、乒乓球、篮球和排球4个项目进行志愿者服务,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有180种;
④
 ,
,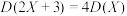 .
.| A.②③ | B.②③④ | C.①②④ | D.①② |
您最近一年使用:0次
2023-09-17更新
|
811次组卷
|
5卷引用:福建省福州市六校2023-2024学年高二下学期期末联考数学试题
福建省福州市六校2023-2024学年高二下学期期末联考数学试题四川省成都市田家炳中学2024届高三第一次月考理科数学试题(已下线)第十章 计数原理、概率、随机变量及其分布(测试)(已下线)7.5 正态分布 (分层作业)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第三册)(已下线)高二数学下学期期末押题试卷01
名校
解题方法
4 . 某地推动乡村振兴发展,推广柑橘种植,经品种改良,农民经济收入显著提高.为了解改良效果,合作社工作人员在该农村地区2000棵果树抽取20棵测量果实平均直径(单位:cm).得到数据如下:
7.11 7.35 6.93 7.11 7.06 7.23 7.16 7.05 7.12 7.09
6.87 7.19 7.12 7.08 7.12 7.11 7.25 6.99 7.12 7.14
根据经验,果实平均直径服从正态分布 ,以样本平均数
,以样本平均数 作为
作为 的估计值
的估计值 ,样本标准差
,样本标准差 作为
作为 的估计值
的估计值 .为提高果实品质,需要将直径小于
.为提高果实品质,需要将直径小于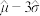 的果实提前去除,果实直径大于7.2cm的即为优果,在该种培育方法下,平均每棵果树结果50个.经计算得
的果实提前去除,果实直径大于7.2cm的即为优果,在该种培育方法下,平均每棵果树结果50个.经计算得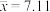 ,
,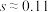 .
.
(1)估计优果的个数;
(2)为进一步提升柑橘质量,需要清除果实较小的果树,专家建议在每棵果树中抽取 个测量果实直径,如果出现果实小于
个测量果实直径,如果出现果实小于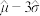 的果实,则认为该果树为果实较小.
的果实,则认为该果树为果实较小.
(ⅰ)试说明此种方案犯错误的概率会随着摘取果实数的增加而增加;
(ⅱ)根据小概率值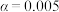 及(ⅰ)中结论确定
及(ⅰ)中结论确定 的值,估计该地所有果树中需要检验的果实的总个数.
的值,估计该地所有果树中需要检验的果实的总个数.
附:若 ,则
,则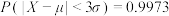 ;
;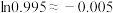 ,
, .
.
7.11 7.35 6.93 7.11 7.06 7.23 7.16 7.05 7.12 7.09
6.87 7.19 7.12 7.08 7.12 7.11 7.25 6.99 7.12 7.14
根据经验,果实平均直径服从正态分布
 ,以样本平均数
,以样本平均数 作为
作为 的估计值
的估计值 ,样本标准差
,样本标准差 作为
作为 的估计值
的估计值 .为提高果实品质,需要将直径小于
.为提高果实品质,需要将直径小于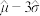 的果实提前去除,果实直径大于7.2cm的即为优果,在该种培育方法下,平均每棵果树结果50个.经计算得
的果实提前去除,果实直径大于7.2cm的即为优果,在该种培育方法下,平均每棵果树结果50个.经计算得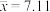 ,
,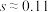 .
.(1)估计优果的个数;
(2)为进一步提升柑橘质量,需要清除果实较小的果树,专家建议在每棵果树中抽取
 个测量果实直径,如果出现果实小于
个测量果实直径,如果出现果实小于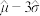 的果实,则认为该果树为果实较小.
的果实,则认为该果树为果实较小.(ⅰ)试说明此种方案犯错误的概率会随着摘取果实数的增加而增加;
(ⅱ)根据小概率值
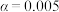 及(ⅰ)中结论确定
及(ⅰ)中结论确定 的值,估计该地所有果树中需要检验的果实的总个数.
的值,估计该地所有果树中需要检验的果实的总个数.附:若
 ,则
,则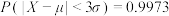 ;
;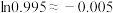 ,
, .
.
您最近一年使用:0次
2023-01-02更新
|
377次组卷
|
2卷引用:福建省厦门双十中学2024届高三下学期高考热身考试数学试题
名校
5 . 某大学为了了解数学专业研究生招生的情况,对近五年的报考人数进行了统计,得到如下统计数据:
(1)经分析, 与
与 存在显著的线性相关性,求
存在显著的线性相关性,求 关于
关于 的线性回归方程
的线性回归方程 并预测
并预测 年(按
年(按 计算)的报考人数;
计算)的报考人数;
(2)每年报考该专业研究生的考试成绩大致符合正态分布 ,根据往年统计数据,
,根据往年统计数据,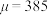 ,
,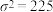 ,录取方案:总分在
,录取方案:总分在 分以上的直接录取;总分在
分以上的直接录取;总分在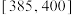 之间的进入面试环节,录取其中的
之间的进入面试环节,录取其中的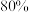 ;低于
;低于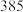 分的不予录取,请预测
分的不予录取,请预测 年该专业录取的大约人数(最后结果四舍五入,保留整数).
年该专业录取的大约人数(最后结果四舍五入,保留整数).
参考公式和数据: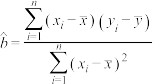 ,
, ,
,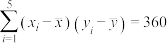 .
.
若随机变量 ,则
,则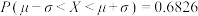 ,
,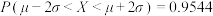 ,
,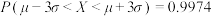 .
.
| 2015 | 2016 | 2017 | 2018 | 2019 | |
| 年份x | 1 | 2 | 3 | 4 | 5 |
| 报考人数y | 30 | 60 | 100 | 140 | 170 |
 与
与 存在显著的线性相关性,求
存在显著的线性相关性,求 关于
关于 的线性回归方程
的线性回归方程 并预测
并预测 年(按
年(按 计算)的报考人数;
计算)的报考人数;(2)每年报考该专业研究生的考试成绩大致符合正态分布
 ,根据往年统计数据,
,根据往年统计数据,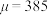 ,
,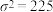 ,录取方案:总分在
,录取方案:总分在 分以上的直接录取;总分在
分以上的直接录取;总分在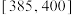 之间的进入面试环节,录取其中的
之间的进入面试环节,录取其中的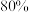 ;低于
;低于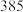 分的不予录取,请预测
分的不予录取,请预测 年该专业录取的大约人数(最后结果四舍五入,保留整数).
年该专业录取的大约人数(最后结果四舍五入,保留整数).参考公式和数据:
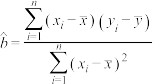 ,
, ,
,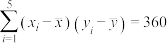 .
.若随机变量
 ,则
,则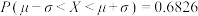 ,
,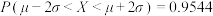 ,
,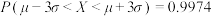 .
.
您最近一年使用:0次
2022-09-23更新
|
346次组卷
|
9卷引用:福建省福州屏东中学2022届高三上学期开学考试数学试题
福建省福州屏东中学2022届高三上学期开学考试数学试题山东省德州市2019-2020学年高二下学期期末考试数学试题江苏省南京、镇江市部分名校2021-2022学年高二下学期5月学情调查考试数学试题黑龙江省哈尔滨市第三中学校2021-2022学年高二下学期期末考试数学试题(已下线)数学建模-预测与估计问题四川省凉山州宁南中学2022-2023学年高二下学期第一次月考理科数学试题内蒙古自治区通辽市科尔沁左翼中旗实验高级中学2023-2024学年高二下学期7月期末数学试题安徽省马鞍山市第二中学2023届高三上学期10月阶段性测试数学试题(已下线)第五章 概率统计创新问题 专题四 数学建模与概率统计 微点1 数学建模与概率统计(一)【培优版】
6 . 南平市于2018年成功获得2022年第十七届福建省运会承办权.为进一步提升第十七届福建省运会志愿者综合素质,提高志愿者服务能力,南平市启动首批志愿者通识培训,并于培训后对参训志愿者进行了一次测试,通过随机抽样,得到100名参训志愿者的测试成绩,统计结果整理得到如图所示的频率分布直方图.
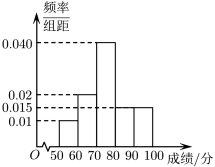
(1)由频率分布直方图可以认为,此次测试成绩 近似于服从正态分布
近似于服从正态分布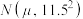 ,
, 近似为这100人测试成绩的平均值(同一组中的数据用该组区间的中点值作代表),
近似为这100人测试成绩的平均值(同一组中的数据用该组区间的中点值作代表),
①求 的值;
的值;
②利用该正态分布,求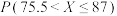 ;
;
(2)在(1)的条件下,主办单位为此次参加测试的志愿者制定如下奖励方案:①测试成绩不低于 的可以获赠2次随机话费,测试成绩低于
的可以获赠2次随机话费,测试成绩低于 的可以获赠1次随机话费;
的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
今在此次参加测试的志愿者中随机抽取一名,记该志愿者获赠的话费为 (单位:元),试根据样本估计总体的思想,求
(单位:元),试根据样本估计总体的思想,求 的分布列与数学期望.
的分布列与数学期望.
参考数据与公式:若 ,则
,则 ,
,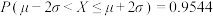 ,
,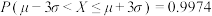 .
.

(1)由频率分布直方图可以认为,此次测试成绩
 近似于服从正态分布
近似于服从正态分布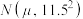 ,
, 近似为这100人测试成绩的平均值(同一组中的数据用该组区间的中点值作代表),
近似为这100人测试成绩的平均值(同一组中的数据用该组区间的中点值作代表),①求
 的值;
的值;②利用该正态分布,求
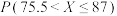 ;
;(2)在(1)的条件下,主办单位为此次参加测试的志愿者制定如下奖励方案:①测试成绩不低于
 的可以获赠2次随机话费,测试成绩低于
的可以获赠2次随机话费,测试成绩低于 的可以获赠1次随机话费;
的可以获赠1次随机话费;②每次获赠的随机话费和对应的概率为:
| 赠送话费的金额(元) | 10 | 30 |
| 概率 |  |  |
 (单位:元),试根据样本估计总体的思想,求
(单位:元),试根据样本估计总体的思想,求 的分布列与数学期望.
的分布列与数学期望.参考数据与公式:若
 ,则
,则 ,
,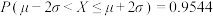 ,
,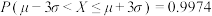 .
.
您最近一年使用:0次
2022-05-08更新
|
1746次组卷
|
5卷引用:福建省南平市2022届高三毕业班第三次质量检测数学试题
福建省南平市2022届高三毕业班第三次质量检测数学试题(已下线)专题12 四大分布:两点分布、超几何分布、二项分布、正态分布-2021-2022学年高二数学下学期期末必考题型归纳及过关测试(人教A版2019)(已下线)考点27 随机变量的分布列、期望与方差(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)(已下线)专题14 统计广东省汕头市潮阳一中明光学校2024届高三上学期11月期中数学试题
解题方法
7 . 《福建省高考改革试点方案》规定:从2018年秋季高中入学的新生开始,不分文理科;2021年高考总成绩由语数外三门统考科目和物理、化学等六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为A、B、C、D、E共5个等级,参照正态分布原则,确定各等级人数所占比例分别为15%、35%、35%、13%、2%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到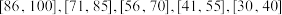 五个分数区间,得到考生的等级成绩.某市高一学生共6000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩
五个分数区间,得到考生的等级成绩.某市高一学生共6000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩 大致服从正态分布
大致服从正态分布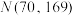 .
.
(1)求该市化学原始成绩在区间 的人数;
的人数;
(2)以各等级人数所占比例作为各分数区间发生的概率,按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间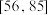 的人数,求
的人数,求
(附:若随机变量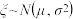 ,则
,则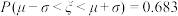 ,
, ,
,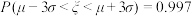 )
)
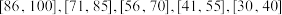 五个分数区间,得到考生的等级成绩.某市高一学生共6000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩
五个分数区间,得到考生的等级成绩.某市高一学生共6000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩 大致服从正态分布
大致服从正态分布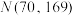 .
.(1)求该市化学原始成绩在区间
 的人数;
的人数;(2)以各等级人数所占比例作为各分数区间发生的概率,按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间
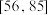 的人数,求
的人数,求
(附:若随机变量
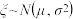 ,则
,则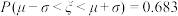 ,
, ,
,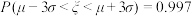 )
)
您最近一年使用:0次
名校
8 . 在创建“全国文明卫生城”过程中,某市“创城办”为了调查市民对创城工作的了解情况,进行了一次创城知识问卷调查(一位市民只能参加一次).通过随机抽样,得到参加问卷调查的1000人的得分(满分100分)统计结果如下表所示.
(1)由频数分布表可以大致认为,此次问卷调查的得分 服从正态分布
服从正态分布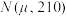 ,
, 近似为这1000人得分的平均值(同一组数据用该组数据区间的中点值表示),请用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组数据区间的中点值表示),请用正态分布的知识求 ;
;
(2)在(1)的条件下,“创城办”为此次参加问卷调查的市民制定如下奖励方案:
(ⅰ)得分不低于 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ⅱ)每次获赠送的随机话费和对应的概率为:
现有市民甲要参加此次问卷调查,记 (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求 的分布列与数学期望.
的分布列与数学期望.
参考数据与公式: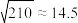 ,若
,若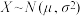 ,则①
,则①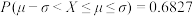 ;②
;②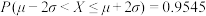 ;③
;③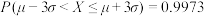 .
.
组别 | 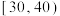 | 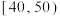 |  |  |  |  | 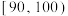 |
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
 服从正态分布
服从正态分布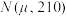 ,
, 近似为这1000人得分的平均值(同一组数据用该组数据区间的中点值表示),请用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组数据区间的中点值表示),请用正态分布的知识求 ;
;(2)在(1)的条件下,“创城办”为此次参加问卷调查的市民制定如下奖励方案:
(ⅰ)得分不低于
 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于 的可以获赠1次随机话费;
的可以获赠1次随机话费;(ⅱ)每次获赠送的随机话费和对应的概率为:
赠送的随机话费(单元:元) | 20 | 40 |
概率 | 0.75 | 0.25 |
 (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求 的分布列与数学期望.
的分布列与数学期望.参考数据与公式:
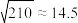 ,若
,若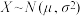 ,则①
,则①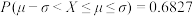 ;②
;②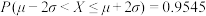 ;③
;③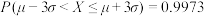 .
.
您最近一年使用:0次
2021-07-28更新
|
2258次组卷
|
22卷引用:福建省2019届高三毕业班数学学科备考关键问题指导系列适应性练习(一)数学(理)试题
福建省2019届高三毕业班数学学科备考关键问题指导系列适应性练习(一)数学(理)试题福建省莆田第一中学2018-2019学年高二下学期期中数学(理)试题福建省师范大学附属中学2024届高三上学期10月月考数学试题福建省莆田市第五中学2024届高三上学期期中数学试题广西桂林、贺州、崇左三市2018届高三第二次联合调研考试数学(理)试题【全国校级联考】江西省重点中学协作体2018届高三第二次联考数学(理)试题(已下线)《高频考点解密》—解密25 概率【全国百强校】湖南省长沙市长郡中学2019届高三上学期第五次调研考试数学(理科)试题【市级联考】山东省德州市2019届高三期末联考数学(理科)试题(已下线)2019年5月12日 《每日一题》理数选修2-3-每周一测湖南省长郡中学2019届高三下学期第一次模拟考试数学(理)试题四川省绵阳南山中学2020届高三三诊模拟数学(理)试题湖北省重点高中联考协作体2018-2019学年高三下学期期中数学(理)试题湖南省衡阳市第八中学2018-2019学年高三下学期第十二次月考数学(理)试题辽宁省大连市2020届高三第二次模拟考试数学理科试题四川省成都市第七中学高中2020届高三下学期高考适应性考试数学(理)试题江西省上高二中2021届高三上学期第二次月考数学(理)试题江西省宜春市上高二中2021届高三(上)第二次月考数学(理科)试题(已下线)2021届高三高考数学适应性测试八省联考考后仿真系列卷三(已下线)解密21 统计与概率 (讲义)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练(已下线)专题03 正态分布-【解题思路培养】2022年高考数学一轮复习解答题拿分秘籍(全国通用版)(已下线)专题7 第1讲 概率、随机变量及其分布列
9 . 《福建省高考改革试点方案》规定:从2018年秋季高中入学的新生开始,不分文理科;2021年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成,将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%、7%、18%、22%、22%、18%、7%、3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100]、[81,90]、[71.80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八个分数区间,得到考生的等级成绩,某校高一年级共2000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩 基本服从正态分布
基本服从正态分布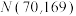 .
.
(1)求化学原始成绩在区间(57,96)的人数;
(2)以各等级人数所占比例作为各分数区间发生的概率,按高考改革方案,若从全省考生中随机抽取3人,记 表示这3人中等级成绩在区间[71,90]的人数,求事件
表示这3人中等级成绩在区间[71,90]的人数,求事件 的概率
的概率
(附:若随机变量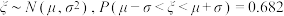 ,
,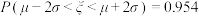 ,
,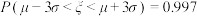 )
)
 基本服从正态分布
基本服从正态分布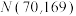 .
.(1)求化学原始成绩在区间(57,96)的人数;
(2)以各等级人数所占比例作为各分数区间发生的概率,按高考改革方案,若从全省考生中随机抽取3人,记
 表示这3人中等级成绩在区间[71,90]的人数,求事件
表示这3人中等级成绩在区间[71,90]的人数,求事件 的概率
的概率(附:若随机变量
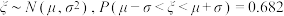 ,
,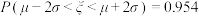 ,
,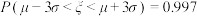 )
)
您最近一年使用:0次



