解题方法
1 . 1799年,哥廷根大学的高斯在其博士论文中证明了如下定理:任何复系数一元 次多项式方程在复数域上至少有一根(
次多项式方程在复数域上至少有一根( ).此定理被称为代数基本定理,在代数乃至整个数学中起着基础作用.由此定理还可以推出以下重要结论:
).此定理被称为代数基本定理,在代数乃至整个数学中起着基础作用.由此定理还可以推出以下重要结论: 次复系数多项式方程在复数域内有且只有
次复系数多项式方程在复数域内有且只有 个根(重根按重数计算).对于
个根(重根按重数计算).对于 次复系数多项式
次复系数多项式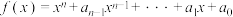 ,其中
,其中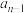 ,
,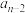 ,
, ,若方程
,若方程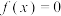 有
有 个复根
个复根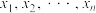 ,则有如下的高阶韦达定理:
,则有如下的高阶韦达定理:
(1)在复数域内解方程 ;
;
(2)若三次方程 的三个根分别是
的三个根分别是 ,
,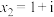 ,
, (
( 为虚数单位),求
为虚数单位),求 ,
, ,
, 的值;
的值;
(3)在 的多项式
的多项式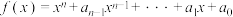 中,已知
中,已知 ,
,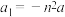 ,
,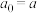 ,
, 为非零实数,且方程
为非零实数,且方程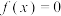 的根恰好全是正实数,求出该方程的所有根(用含
的根恰好全是正实数,求出该方程的所有根(用含 的式子表示).
的式子表示).
 次多项式方程在复数域上至少有一根(
次多项式方程在复数域上至少有一根( ).此定理被称为代数基本定理,在代数乃至整个数学中起着基础作用.由此定理还可以推出以下重要结论:
).此定理被称为代数基本定理,在代数乃至整个数学中起着基础作用.由此定理还可以推出以下重要结论: 次复系数多项式方程在复数域内有且只有
次复系数多项式方程在复数域内有且只有 个根(重根按重数计算).对于
个根(重根按重数计算).对于 次复系数多项式
次复系数多项式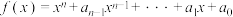 ,其中
,其中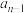 ,
,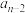 ,
, ,若方程
,若方程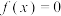 有
有 个复根
个复根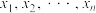 ,则有如下的高阶韦达定理:
,则有如下的高阶韦达定理:
(1)在复数域内解方程
 ;
;(2)若三次方程
 的三个根分别是
的三个根分别是 ,
,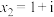 ,
, (
( 为虚数单位),求
为虚数单位),求 ,
, ,
, 的值;
的值;(3)在
 的多项式
的多项式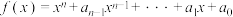 中,已知
中,已知 ,
, ,
,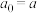 ,
, 为非零实数,且方程
为非零实数,且方程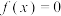 的根恰好全是正实数,求出该方程的所有根(用含
的根恰好全是正实数,求出该方程的所有根(用含 的式子表示).
的式子表示).
您最近一年使用:0次
2 . 对于非空集合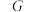 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:
1.(封闭性)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
2.(结合律)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
3.(恒等元)存在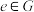 ,使得对任意
,使得对任意 ,
, ;
;
4.(逆的存在性)对任意 ,都存在
,都存在 ,使得
,使得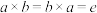 .
.
记群 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意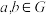 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).
(1)证明:所有实数在普通加法运算下构成群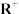 ;
;
(2)记 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群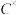 ,并说明理由;
,并说明理由;
(3)所有阶数小于等于四的群 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
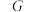 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:1.(封闭性)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;2.(结合律)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;3.(恒等元)存在
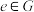 ,使得对任意
,使得对任意 ,
, ;
;4.(逆的存在性)对任意
 ,都存在
,都存在 ,使得
,使得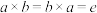 .
.记群
 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意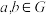 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).(1)证明:所有实数在普通加法运算下构成群
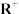 ;
;(2)记
 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群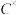 ,并说明理由;
,并说明理由;(3)所有阶数小于等于四的群
 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
您最近一年使用:0次
3 . 数学中的数,除了实数、复数之外,还有四元数.四元数在计算机图形学中有广泛应用,主要用于描述空间中的旋转.集合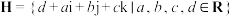 中的元素
中的元素 称为四元数,其中i,j,k都是虚数单位,d称为
称为四元数,其中i,j,k都是虚数单位,d称为 的实部,
的实部,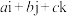 称为
称为 的虚部.两个四元数之间的加法定义为
的虚部.两个四元数之间的加法定义为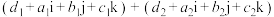
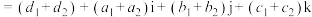 .
.
两个四元数的乘法定义为: ,四元数的乘法具有结合律,且乘法对加法有分配律.对于四元数
,四元数的乘法具有结合律,且乘法对加法有分配律.对于四元数 ,若存在四元数
,若存在四元数 使得
使得 ,称
,称 是
是 的逆,记为
的逆,记为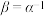 .实部为0的四元数称为纯四元数,把纯四元数的全体记为W.
.实部为0的四元数称为纯四元数,把纯四元数的全体记为W.
(1)设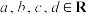 ,四元数
,四元数 .记
.记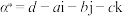 表示
表示 的共轭四元数.
的共轭四元数.
(i)计算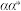 ;
;
(ii)若 ,求
,求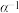 ;
;
(iii)若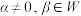 ,证明:
,证明: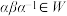 ;
;
(2)在空间直角坐标系中,把空间向量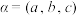 与纯四元数
与纯四元数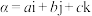 看作同一个数学对象.设
看作同一个数学对象.设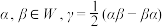 .
.
(i)证明: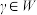 ;
;
(ii)若 是平面X内的两个不共线向量,证明:
是平面X内的两个不共线向量,证明: 是X的一个法向量.
是X的一个法向量.
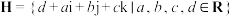 中的元素
中的元素 称为四元数,其中i,j,k都是虚数单位,d称为
称为四元数,其中i,j,k都是虚数单位,d称为 的实部,
的实部,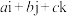 称为
称为 的虚部.两个四元数之间的加法定义为
的虚部.两个四元数之间的加法定义为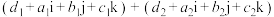
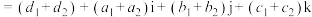 .
.两个四元数的乘法定义为:
 ,四元数的乘法具有结合律,且乘法对加法有分配律.对于四元数
,四元数的乘法具有结合律,且乘法对加法有分配律.对于四元数 ,若存在四元数
,若存在四元数 使得
使得 ,称
,称 是
是 的逆,记为
的逆,记为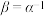 .实部为0的四元数称为纯四元数,把纯四元数的全体记为W.
.实部为0的四元数称为纯四元数,把纯四元数的全体记为W.(1)设
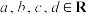 ,四元数
,四元数 .记
.记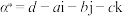 表示
表示 的共轭四元数.
的共轭四元数.(i)计算
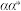 ;
;(ii)若
 ,求
,求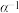 ;
;(iii)若
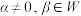 ,证明:
,证明: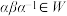 ;
;(2)在空间直角坐标系中,把空间向量
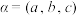 与纯四元数
与纯四元数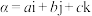 看作同一个数学对象.设
看作同一个数学对象.设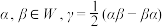 .
.(i)证明:
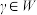 ;
;(ii)若
 是平面X内的两个不共线向量,证明:
是平面X内的两个不共线向量,证明: 是X的一个法向量.
是X的一个法向量.
您最近一年使用:0次
名校
4 . 设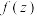 是一个关于复数z的表达式,若
是一个关于复数z的表达式,若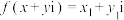 (其中x,y,
(其中x,y, ,
,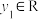

 为虚数单位),就称f将点
为虚数单位),就称f将点 “f对应”到点
“f对应”到点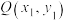 .例如
.例如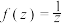 将点
将点 “f对应”到点
“f对应”到点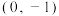 .
.
(1)若 点
点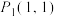 “f对应”到点
“f对应”到点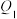 ,点
,点 “f对应”到点
“f对应”到点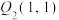 ,求点
,求点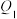 、
、 的坐标;
的坐标;
(2)设常数 ,
,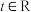 ,若直线l:
,若直线l: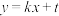 ,
,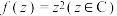 ,是否存在一个有序实数对
,是否存在一个有序实数对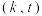 ,使得直线l上的任意一点
,使得直线l上的任意一点 “对应”到点
“对应”到点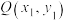 后,点Q仍在直线
后,点Q仍在直线 上?若存在,试求出所有的有序实数对
上?若存在,试求出所有的有序实数对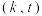 ;若不存在,请说明理由;
;若不存在,请说明理由;
(3)设常数 ,
,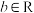 ,集合
,集合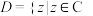 且
且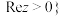 和
和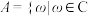 且
且 ,若
,若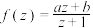 满足:①对于集合D中的任意一个元素z,都有
满足:①对于集合D中的任意一个元素z,都有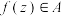 ;②对于集合A中的任意一个元素
;②对于集合A中的任意一个元素 ,都存在集合D中的元素z使得
,都存在集合D中的元素z使得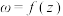 .请写出满足条件的一个有序实数对
.请写出满足条件的一个有序实数对 ,并论证此时的
,并论证此时的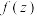 满足条件.
满足条件.
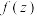 是一个关于复数z的表达式,若
是一个关于复数z的表达式,若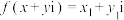 (其中x,y,
(其中x,y, ,
,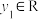

 为虚数单位),就称f将点
为虚数单位),就称f将点 “f对应”到点
“f对应”到点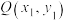 .例如
.例如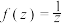 将点
将点 “f对应”到点
“f对应”到点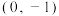 .
.(1)若
 点
点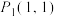 “f对应”到点
“f对应”到点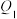 ,点
,点 “f对应”到点
“f对应”到点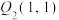 ,求点
,求点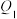 、
、 的坐标;
的坐标;(2)设常数
 ,
,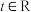 ,若直线l:
,若直线l: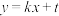 ,
,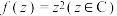 ,是否存在一个有序实数对
,是否存在一个有序实数对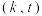 ,使得直线l上的任意一点
,使得直线l上的任意一点 “对应”到点
“对应”到点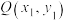 后,点Q仍在直线
后,点Q仍在直线 上?若存在,试求出所有的有序实数对
上?若存在,试求出所有的有序实数对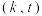 ;若不存在,请说明理由;
;若不存在,请说明理由;(3)设常数
 ,
,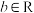 ,集合
,集合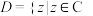 且
且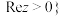 和
和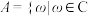 且
且 ,若
,若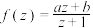 满足:①对于集合D中的任意一个元素z,都有
满足:①对于集合D中的任意一个元素z,都有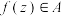 ;②对于集合A中的任意一个元素
;②对于集合A中的任意一个元素 ,都存在集合D中的元素z使得
,都存在集合D中的元素z使得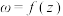 .请写出满足条件的一个有序实数对
.请写出满足条件的一个有序实数对 ,并论证此时的
,并论证此时的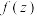 满足条件.
满足条件.
您最近一年使用:0次
2023-07-05更新
|
755次组卷
|
6卷引用:上海市静安区回民中学2024届高三上学期12月阶段性测试数学试题
上海市静安区回民中学2024届高三上学期12月阶段性测试数学试题(已下线)专题01 条件开放型【练】【通用版】湖南省邵阳市第二中学2024届高三下学期入学测试数学试题上海市控江中学2022-2023学年高一下学期期末数学试题(已下线)高一下学期期中数学试卷(提高篇)-举一反三系列浙江省绍兴市第一中学2023-2024学年高一平行班下学期期中考试数学试卷
5 . 意大利数学家卡尔达诺(Cardano.Girolamo,1501-1576)发明了三次方程的代数解法.17世纪人们把卡尔达诺的解法推广并整理为四个步骤:
第一步,把方程 中的
中的 用
用 来替换,得到方程
来替换,得到方程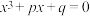 ;
;
第二步,利用公式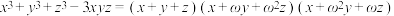 将
将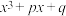 因式分解;
因式分解;
第三步,求得 ,
, 的一组值,得到方程
的一组值,得到方程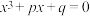 的三个根:
的三个根: ,
,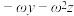 ,
,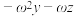 (其中
(其中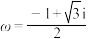 ,
, 为虚数单位);
为虚数单位);
第四步,写出方程 的根:
的根: ,
, ,
, .
.
某同学利用上述方法解方程 时,得到
时,得到 的一个值:
的一个值: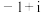 ,则下列说法正确的是( )
,则下列说法正确的是( )
第一步,把方程
 中的
中的 用
用 来替换,得到方程
来替换,得到方程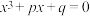 ;
;第二步,利用公式
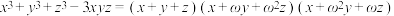 将
将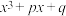 因式分解;
因式分解;第三步,求得
 ,
, 的一组值,得到方程
的一组值,得到方程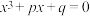 的三个根:
的三个根: ,
,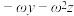 ,
,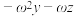 (其中
(其中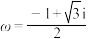 ,
, 为虚数单位);
为虚数单位);第四步,写出方程
 的根:
的根: ,
, ,
, .
.某同学利用上述方法解方程
 时,得到
时,得到 的一个值:
的一个值: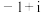 ,则下列说法正确的是( )
,则下列说法正确的是( )A. | B. | C.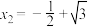 | D. |
您最近一年使用:0次
2022-03-09更新
|
2508次组卷
|
9卷引用:福建省莆田市2022届高三3月第二次教学质量检测数学试题
福建省莆田市2022届高三3月第二次教学质量检测数学试题(已下线)专题16 复数-2022届高考数学一模试题分类汇编(新高考卷)(已下线)考点11 复数(核心考点讲与练)(已下线)专题05 策略开放型【练】【通用版】(已下线)复数的概念与运算山东省齐鲁2021-2022学年3月份高一阶段性质量检测试卷A广东省广州市八校联考2021-2022学年高一下学期期中数学(A卷)试题(已下线)7.2.2 复数的乘、除运算(分层作业)-【上好课】2022-2023学年高一数学同步备课系列(人教A版2019必修第二册)专题07数系的扩充与复数的运算
6 . 设复数 的实部和虚部都是整数,则( )
的实部和虚部都是整数,则( )
 的实部和虚部都是整数,则( )
的实部和虚部都是整数,则( )A.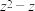 的实部都能被2 整除 的实部都能被2 整除 |
B. 的实部都能被3 整除 的实部都能被3 整除 |
C. 的实部都能被4 整除 的实部都能被4 整除 |
D.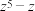 的实部都能被5 整除 的实部都能被5 整除 |
您最近一年使用:0次



