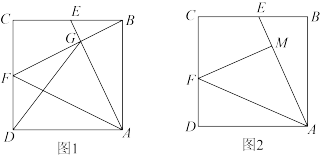
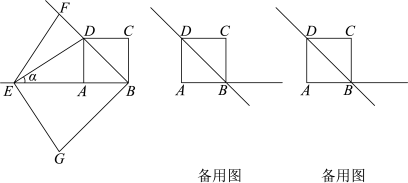
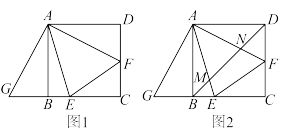
如图,在正方形 中,E,F分别是边
中,E,F分别是边 上的一点,
上的一点, ,连接
,连接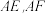 .
. ;
;
(2)如图1,连接 交
交 于点G,连接
于点G,连接 ,若
,若 ,求
,求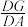 的值;
的值;
(3)如图2,过点F作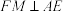 于点M,若
于点M,若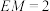 ,
, ,直接写出
,直接写出 的长.
的长.
 中,E,F分别是边
中,E,F分别是边 上的一点,
上的一点, ,连接
,连接 .
.
 ;
;(2)如图1,连接
 交
交 于点G,连接
于点G,连接 ,若
,若 ,求
,求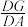 的值;
的值;(3)如图2,过点F作
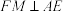 于点M,若
于点M,若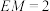 ,
, ,直接写出
,直接写出 的长.
的长.
22-23八年级下·湖北武汉·期末 查看更多[2]
湖北省武汉市新洲区2022--2023学年八年级下学期期末数学试题(已下线)专题04中位线与直角三角形斜边上的中线(三大题型)-【好题汇编】备战2023-2024学年八年级数学下学期期末真题分类汇编(湖北专用)
更新时间:2023/07/03 13:50:38
|
相似题推荐
解答题-证明题
|
适中
(0.65)
名校
【推荐1】如图1,在正方形 中,点
中,点 是直线
是直线 上一点,点
上一点,点 是直线
是直线 上一点(
上一点( 与
与 不重合),
不重合), ,作点
,作点 关于直线
关于直线 的对称点
的对称点 ,连接
,连接 ,
,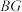 .
. 在线段
在线段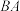 的延长线上,点
的延长线上,点 在线段
在线段 的延长线上,
的延长线上,
①记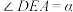 ,求
,求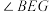 的度数(用含
的度数(用含 的式子表示);
的式子表示);
②用等式表示 ,
, ,
,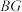 之间的数量关系,并证明;
之间的数量关系,并证明;
(2)当点 在射线
在射线 上,点
上,点 在直线
在直线 上时,直接用等式表示
上时,直接用等式表示 ,
, ,
,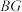 之间的数量关系.
之间的数量关系.
 中,点
中,点 是直线
是直线 上一点,点
上一点,点 是直线
是直线 上一点(
上一点( 与
与 不重合),
不重合), ,作点
,作点 关于直线
关于直线 的对称点
的对称点 ,连接
,连接 ,
,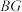 .
.
 在线段
在线段 的延长线上,点
的延长线上,点 在线段
在线段 的延长线上,
的延长线上,①记
 ,求
,求 的度数(用含
的度数(用含 的式子表示);
的式子表示);②用等式表示
 ,
, ,
,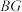 之间的数量关系,并证明;
之间的数量关系,并证明;(2)当点
 在射线
在射线 上,点
上,点 在直线
在直线 上时,直接用等式表示
上时,直接用等式表示 ,
, ,
,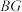 之间的数量关系.
之间的数量关系.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
名校
【推荐2】【建立模型】
如图1,等腰 中,
中, ,
, ,直线
,直线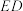 经过点C,过点A作
经过点C,过点A作 于点D,过点B作
于点D,过点B作 于点E,可证明得到
于点E,可证明得到 .
.
【模型应用】

(1)如图2,直线 与x轴、y轴分别交于A、B两点,经过点B作
与x轴、y轴分别交于A、B两点,经过点B作 .点C在第一象限且在直线
.点C在第一象限且在直线 上,
上, ,求点C的坐标;
,求点C的坐标;
(2)在(1)的条件下,求直线 的表达式;
的表达式;
(3)如图3,在平面直角坐标系中,已知点 ,连接
,连接 ,在第二象限内是否存在一点Q,使得
,在第二象限内是否存在一点Q,使得 是以
是以 为直角边的等腰直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
为直角边的等腰直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
如图1,等腰
 中,
中, ,
, ,直线
,直线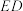 经过点C,过点A作
经过点C,过点A作 于点D,过点B作
于点D,过点B作 于点E,可证明得到
于点E,可证明得到 .
.【模型应用】

(1)如图2,直线
 与x轴、y轴分别交于A、B两点,经过点B作
与x轴、y轴分别交于A、B两点,经过点B作 .点C在第一象限且在直线
.点C在第一象限且在直线 上,
上, ,求点C的坐标;
,求点C的坐标;(2)在(1)的条件下,求直线
 的表达式;
的表达式;(3)如图3,在平面直角坐标系中,已知点
 ,连接
,连接 ,在第二象限内是否存在一点Q,使得
,在第二象限内是否存在一点Q,使得 是以
是以 为直角边的等腰直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
为直角边的等腰直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
【推荐1】如图, 是
是 的直径,点B在线段
的直径,点B在线段 的延长线上,直线
的延长线上,直线 与
与 相切于点D.连接
相切于点D.连接 .
.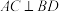 ,交
,交 延长线于点C(保留作图痕迹,不写作法);
延长线于点C(保留作图痕迹,不写作法);
(2)①求证: 平分
平分 ;
;
②若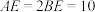 ,求
,求 的长.
的长.
 是
是 的直径,点B在线段
的直径,点B在线段 的延长线上,直线
的延长线上,直线 与
与 相切于点D.连接
相切于点D.连接 .
.
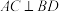 ,交
,交 延长线于点C(保留作图痕迹,不写作法);
延长线于点C(保留作图痕迹,不写作法);(2)①求证:
 平分
平分 ;
;②若
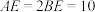 ,求
,求 的长.
的长.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
真题
【推荐2】如图,平面直角坐标系 中,
中,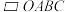 的边
的边 在
在 轴上,对角线
轴上,对角线 ,
, 交于点
交于点 ,函数
,函数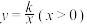 的图象经过点
的图象经过点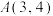 和点
和点 .
.

(1)求 的值和点
的值和点 的坐标;
的坐标;
(2)求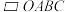 的周长.
的周长.
 中,
中, 的边
的边 在
在 轴上,对角线
轴上,对角线 ,
, 交于点
交于点 ,函数
,函数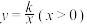 的图象经过点
的图象经过点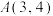 和点
和点 .
.
(1)求
 的值和点
的值和点 的坐标;
的坐标;(2)求
 的周长.
的周长.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
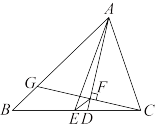
【推荐1】如图, 中,
中, 分别是其角平分线和中线,过点
分别是其角平分线和中线,过点 作
作 于
于 ,交
,交 于
于 ,连接
,连接 ,求线段
,求线段 的长.
的长.
 中,
中, 分别是其角平分线和中线,过点
分别是其角平分线和中线,过点 作
作 于
于 ,交
,交 于
于 ,连接
,连接 ,求线段
,求线段 的长.
的长.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
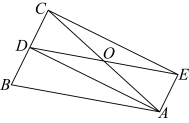
【推荐2】如图,在△ABC中,AB=AC,D为边BC的中点,四边形ABDE是平行四边形,AC,DE相交于点O.
(1)求证:四边形ADCE是矩形;
(2)若∠AOE=60°,AE=2,求矩形ADCE对角线的长.
(1)求证:四边形ADCE是矩形;
(2)若∠AOE=60°,AE=2,求矩形ADCE对角线的长.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
【推荐1】如图,在边长为 的正方形
的正方形 中,点
中,点 为对角线
为对角线 上任意一点(可与
上任意一点(可与 ,
, 重合),连接
重合),连接 ,将线段
,将线段 绕点
绕点 逆时针旋转
逆时针旋转 得到线段
得到线段 ,连接
,连接 ,
, .
.
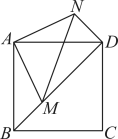
(1)求证: ;
;
(2)当 时,求
时,求 的长.
的长.
 的正方形
的正方形 中,点
中,点 为对角线
为对角线 上任意一点(可与
上任意一点(可与 ,
, 重合),连接
重合),连接 ,将线段
,将线段 绕点
绕点 逆时针旋转
逆时针旋转 得到线段
得到线段 ,连接
,连接 ,
,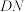 .
.
(1)求证:
 ;
;(2)当
 时,求
时,求 的长.
的长.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
【推荐2】如图, 中,
中, ,
, 是斜边
是斜边 上的中线,点E是
上的中线,点E是 的中点,过点C作
的中点,过点C作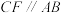 交
交 的延长线于点F,连接
的延长线于点F,连接 .
. ;
;
(2)①当线段 、
、 满足什么数量关系时,四边形
满足什么数量关系时,四边形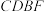 是正方形,并说明理由;
是正方形,并说明理由;
②已知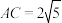 ,
,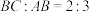 ,求四边形
,求四边形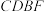 的面积.
的面积.
 中,
中, ,
, 是斜边
是斜边 上的中线,点E是
上的中线,点E是 的中点,过点C作
的中点,过点C作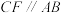 交
交 的延长线于点F,连接
的延长线于点F,连接 .
.
 ;
;(2)①当线段
 、
、 满足什么数量关系时,四边形
满足什么数量关系时,四边形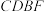 是正方形,并说明理由;
是正方形,并说明理由;②已知
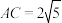 ,
,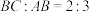 ,求四边形
,求四边形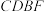 的面积.
的面积.
您最近一年使用:0次

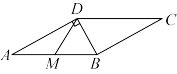
 中,
中, 交
交 的平分线
的平分线 ,交
,交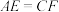 .
.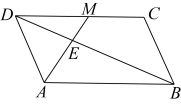
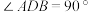 ,点
,点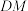 .
.
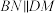 ,交
,交 (尺规作图,不写作法,保留作图痕迹);
(尺规作图,不写作法,保留作图痕迹);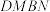 为菱形;
为菱形; ,求四边形
,求四边形
 交
交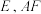 交
交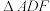 绕点
绕点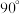 得到
得到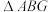 .
.
 ;
;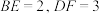 ,求
,求 的面积;
的面积; 于点
于点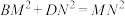 .
.


