如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
(1)求证:DB平分∠ADC;
(2)若CD=9,tan∠ABE= ,求⊙O的半径.
,求⊙O的半径.
(1)求证:DB平分∠ADC;
(2)若CD=9,tan∠ABE=
 ,求⊙O的半径.
,求⊙O的半径.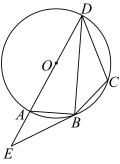
更新时间:2020/01/21 20:04:58
|
相似题推荐
解答题-计算题
|
适中
(0.65)
【推荐1】阅读下列材料:
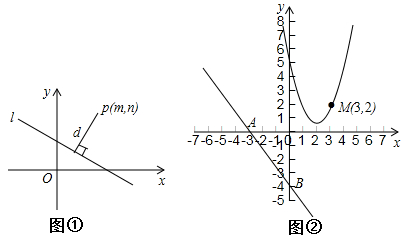
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+By+C=0(A,B,C是常数,且A,B不同时为0).如图①,点P(m,n)到直线l:Ax+By+C=0的距离(d)计算公式是d=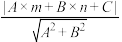 .
.
例:求点P(1,2)到直线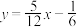 的距离d时,先将
的距离d时,先将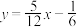 化为5x-12y-2=0,再由上述距离公式求得
化为5x-12y-2=0,再由上述距离公式求得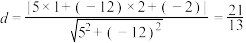 .
.
解答下列问题:
如图②,已知直线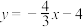 与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
(1)求点M到直线AB的距离;
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+By+C=0(A,B,C是常数,且A,B不同时为0).如图①,点P(m,n)到直线l:Ax+By+C=0的距离(d)计算公式是d=
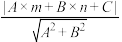 .
.
例:求点P(1,2)到直线
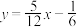 的距离d时,先将
的距离d时,先将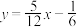 化为5x-12y-2=0,再由上述距离公式求得
化为5x-12y-2=0,再由上述距离公式求得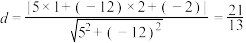 .
.解答下列问题:
如图②,已知直线
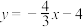 与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).(1)求点M到直线AB的距离;
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
【推荐2】已知 的半径为
的半径为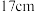 ,弦
,弦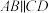 ,
,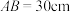 ,圆心
,圆心 位于
位于 、
、 的同侧,
的同侧,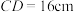 ,求
,求 与
与 之间的距离.
之间的距离.
 的半径为
的半径为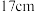 ,弦
,弦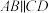 ,
,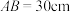 ,圆心
,圆心 位于
位于 、
、 的同侧,
的同侧,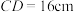 ,求
,求 与
与 之间的距离.
之间的距离.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
【推荐1】已知OA,OB是⊙O的半径,且OA⊥OB,垂足为O,P是射线OA上的一点(点A除外),直线BP交⊙O于点Q,过Q作⊙O的切线交射线OA于点E.

(1)如图①,点P在线段OA上,若∠OBQ=15°,求∠AQE的大小;
(2)如图②,点P在OA的延长线上,若∠OBQ=65°,求∠AQE的大小.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
【推荐2】如图, 中,
中, ,以
,以 为直径的
为直径的 分别交边
分别交边 ,
, 于点
于点 ,
, ,过点
,过点 作
作 的切线交
的切线交 的延长线于点
的延长线于点 .
. ;
;
(2)若 ,
, ,求
,求 和
和 的长.
的长.
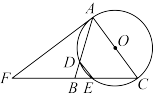
 中,
中, ,以
,以 为直径的
为直径的 分别交边
分别交边 ,
, 于点
于点 ,
, ,过点
,过点 作
作 的切线交
的切线交 的延长线于点
的延长线于点 .
.
 ;
;(2)若
 ,
, ,求
,求 和
和 的长.
的长.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
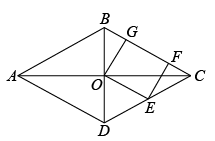
【推荐1】如图,四边形 是一个风筝的框架示意图,G为
是一个风筝的框架示意图,G为 的中点,四边形
的中点,四边形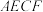 为菱形,
为菱形, .
.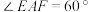 ,求证:四边形
,求证:四边形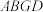 是菱形;
是菱形;
(2)若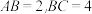 ,求菱形
,求菱形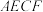 的面积.
的面积.
 是一个风筝的框架示意图,G为
是一个风筝的框架示意图,G为 的中点,四边形
的中点,四边形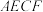 为菱形,
为菱形, .
.

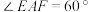 ,求证:四边形
,求证:四边形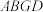 是菱形;
是菱形;(2)若
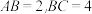 ,求菱形
,求菱形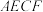 的面积.
的面积.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
名校
【推荐2】如图,在 中,
中, ,以
,以 为直径的
为直径的 分别交
分别交 、
、 于点
于点 、
、 .点
.点 在
在 的延长线上,且
的延长线上,且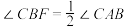 .
. 是
是 的切线;
的切线;
(2)若 ,
, ,求
,求 的长.
的长.
 中,
中, ,以
,以 为直径的
为直径的 分别交
分别交 、
、 于点
于点 、
、 .点
.点 在
在 的延长线上,且
的延长线上,且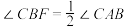 .
.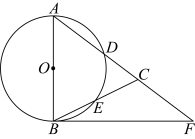
 是
是 的切线;
的切线;(2)若
 ,
, ,求
,求 的长.
的长.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
【推荐1】综合与实践
课本再现
(1)如图1,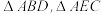 都是等边三角形.
都是等边三角形.
① 与
与 有什么关系?请用旋转的性质说明上述关系.
有什么关系?请用旋转的性质说明上述关系. 中,
中, 的长度与
的长度与 之间存在一定的关系,可考虑通过旋转构造特殊三角形之间的全等或相似求解.
之间存在一定的关系,可考虑通过旋转构造特殊三角形之间的全等或相似求解.
特例感知
②若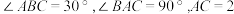 ,则
,则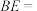 .
.
请你尝试解决以下问题:
类比应用
(2)如图2,在四边形 中,
中, ,
, 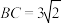 ,求
,求 的长.
的长.
(3)如图3,在四边形 中,
中,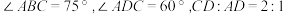 ,
, ,直接写出
,直接写出 的长.
的长.
课本再现
(1)如图1,
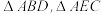 都是等边三角形.
都是等边三角形.①
 与
与 有什么关系?请用旋转的性质说明上述关系.
有什么关系?请用旋转的性质说明上述关系.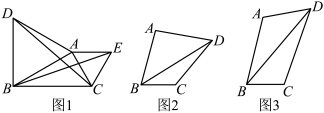
 中,
中, 的长度与
的长度与 之间存在一定的关系,可考虑通过旋转构造特殊三角形之间的全等或相似求解.
之间存在一定的关系,可考虑通过旋转构造特殊三角形之间的全等或相似求解.特例感知
②若
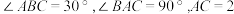 ,则
,则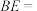 .
.请你尝试解决以下问题:
类比应用
(2)如图2,在四边形
 中,
中, ,
, 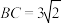 ,求
,求 的长.
的长.(3)如图3,在四边形
 中,
中,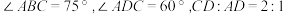 ,
, ,直接写出
,直接写出 的长.
的长.
您最近一年使用:0次
解答题-作图题
|
适中
(0.65)
【推荐2】问题:如果α,β都为锐角,且tanα= ,tanβ=
,tanβ= ,求α+β的度数.
,求α+β的度数.
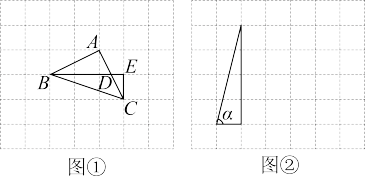
解决:如图①,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,连结AC,易证△ABC是等腰直角三角形,因此可求得α+β=∠ABC= .
拓展:参考以上方法,解决下列问题:如果α,β都为锐角,当tanα=4,tanβ= 时,
时,
(1)在图②的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β;
(2)求出α﹣β= °.
 ,tanβ=
,tanβ= ,求α+β的度数.
,求α+β的度数.
解决:如图①,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,连结AC,易证△ABC是等腰直角三角形,因此可求得α+β=∠ABC= .
拓展:参考以上方法,解决下列问题:如果α,β都为锐角,当tanα=4,tanβ=
 时,
时,(1)在图②的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β;
(2)求出α﹣β= °.
您最近一年使用:0次

 中,点
中,点 的坐标分别为
的坐标分别为 ,点
,点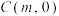 是x正半轴上一个动点,
是x正半轴上一个动点,
 时,写出线段
时,写出线段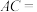 _____,
_____, _____.
_____. 是
是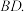
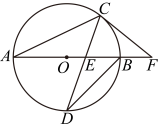
 ;
;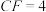 ,
,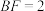 ,求
,求