20-21高一·全国·课后作业
1 . 画一个六面体:
(1)使它是一个四棱柱;
(2)使它是由两个三棱锥组成的;
(3)使它是五棱锥.
(1)使它是一个四棱柱;
(2)使它是由两个三棱锥组成的;
(3)使它是五棱锥.
您最近一年使用:0次
20-21高一·全国·课后作业
2 . 按下列条件分割三棱台ABC-A1B1C1(不需要画图,各写出一种分割方法即可).

(1)一个三棱柱和一个多面体;
(2)三个三棱锥.

(1)一个三棱柱和一个多面体;
(2)三个三棱锥.
您最近一年使用:0次
3 . 是否存在既没有面对角线也没有体对角线的多面体?如果存在,请举出实例;如果不存在,请说明理由.
您最近一年使用:0次
2020-01-31更新
|
356次组卷
|
4卷引用:第十一章 立体几何初步 11.1 空间几何体 11.1.3 多面体与棱柱
(已下线)第十一章 立体几何初步 11.1 空间几何体 11.1.3 多面体与棱柱(已下线)第1课时 课后 基本立体图形-棱柱、棱锥、棱台人教B版(2019) 必修第四册 逆袭之路 第十一章 立体几何初步 11.1.3 多面体与棱柱人教B版(2019)必修第四册课本习题11.1.3 多面体与棱柱
4 . 正多面体也称柏拉图立体,被誉为最有规律的立体结构,其所有面都只由一种正多边形构成的多面体(各面都是全等的正多边形,且每一个顶点所接的面数都一样,各相邻面所成二面角都相等).数学家已经证明世界上只存在五种柏拉图立体,即正四面体、正六面体、正八面体、正十二面体、正二十面体.已知一个正四面体 和一个正八面体
和一个正八面体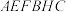 的棱长都是
的棱长都是 (如图),把它们拼接起来,使它们一个表面重合,得到一个新多面体.
(如图),把它们拼接起来,使它们一个表面重合,得到一个新多面体.
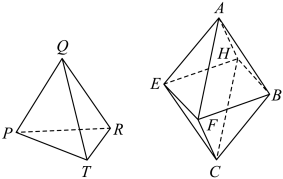
(1)求新多面体的体积;
(2)求正八面体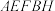 中二面角
中二面角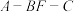 的余弦值;
的余弦值;
(3)判断新多面体为几面体?(只需给出答案,无需证明)
 和一个正八面体
和一个正八面体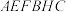 的棱长都是
的棱长都是 (如图),把它们拼接起来,使它们一个表面重合,得到一个新多面体.
(如图),把它们拼接起来,使它们一个表面重合,得到一个新多面体.
(1)求新多面体的体积;
(2)求正八面体
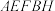 中二面角
中二面角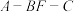 的余弦值;
的余弦值;(3)判断新多面体为几面体?(只需给出答案,无需证明)
您最近一年使用:0次
20-21高二·全国·课后作业
5 . 记A为所有多面体组成的集合,B为所有棱柱组成的集合,C为所有直棱柱组成的集合,D为所有正棱柱组成的集合,写出集合A,B,C,D之间的关系.
您最近一年使用:0次
20-21高一·全国·课后作业
6 . 画一个五面体.
您最近一年使用:0次
7 . 用符号表示出图中所示多面体的所有顶点、棱、面.
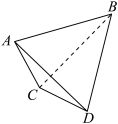
您最近一年使用:0次
2020-01-31更新
|
256次组卷
|
3卷引用:第十一章 立体几何初步 11.1 空间几何体 11.1.3 多面体与棱柱
(已下线)第十一章 立体几何初步 11.1 空间几何体 11.1.3 多面体与棱柱人教B版(2019) 必修第四册 逆袭之路 第十一章 立体几何初步 11.1.3 多面体与棱柱人教B版(2019)必修第四册课本习题11.1.3 多面体与棱柱
8 . 圆柱是不是多面体?为什么?
您最近一年使用:0次
2020-01-31更新
|
241次组卷
|
3卷引用:第十一章 立体几何初步 11.1 空间几何体 11.1.3 多面体与棱柱
(已下线)第十一章 立体几何初步 11.1 空间几何体 11.1.3 多面体与棱柱人教B版(2019) 必修第四册 逆袭之路 第十一章 立体几何初步 11.1.3 多面体与棱柱人教B版(2019)必修第四册课本习题11.1.3 多面体与棱柱
9 . 举出点运动的轨迹是线、线运动的轨迹是面、面运动的轨迹是体的实例.
您最近一年使用:0次



