解题方法
1 . 在空间直角坐标系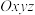 中,过点
中,过点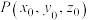 且以
且以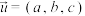 为方向向量的直线方程可表示为
为方向向量的直线方程可表示为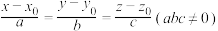 ,过点
,过点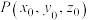 且以
且以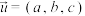 为法向量的平面方程可表示为
为法向量的平面方程可表示为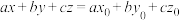 .
.
(1)若直线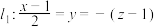 与
与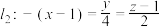 都在平面
都在平面 内,求平面
内,求平面 的方程;
的方程;
(2)在三棱柱 中,点
中,点 与坐标原点
与坐标原点 重合,点
重合,点 在平面
在平面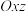 内,平面
内,平面 以
以 为法向量,平面
为法向量,平面 的方程为
的方程为 ,求点
,求点 的坐标;
的坐标;
(3)若集合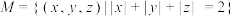 中所有的点构成了多面体
中所有的点构成了多面体 的各个面,求
的各个面,求 的体积和相邻两个面所在平面的夹角的余弦值.
的体积和相邻两个面所在平面的夹角的余弦值.
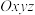 中,过点
中,过点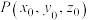 且以
且以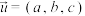 为方向向量的直线方程可表示为
为方向向量的直线方程可表示为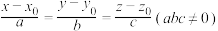 ,过点
,过点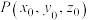 且以
且以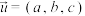 为法向量的平面方程可表示为
为法向量的平面方程可表示为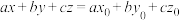 .
.(1)若直线
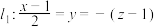 与
与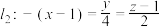 都在平面
都在平面 内,求平面
内,求平面 的方程;
的方程;(2)在三棱柱
 中,点
中,点 与坐标原点
与坐标原点 重合,点
重合,点 在平面
在平面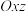 内,平面
内,平面 以
以 为法向量,平面
为法向量,平面 的方程为
的方程为 ,求点
,求点 的坐标;
的坐标;(3)若集合
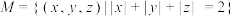 中所有的点构成了多面体
中所有的点构成了多面体 的各个面,求
的各个面,求 的体积和相邻两个面所在平面的夹角的余弦值.
的体积和相邻两个面所在平面的夹角的余弦值.
您最近一年使用:0次
2 . 已知正八面体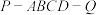 的所有棱长均为
的所有棱长均为 ,将其沿平面
,将其沿平面 切开后分成
切开后分成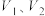 两部分,将
两部分,将 沿直线
沿直线 方向平移至
方向平移至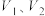 的底面距离为
的底面距离为 且
且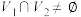 ,则
,则 与
与 公共部分的体积为:( ).
公共部分的体积为:( ).
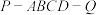 的所有棱长均为
的所有棱长均为 ,将其沿平面
,将其沿平面 切开后分成
切开后分成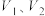 两部分,将
两部分,将 沿直线
沿直线 方向平移至
方向平移至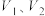 的底面距离为
的底面距离为 且
且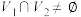 ,则
,则 与
与 公共部分的体积为:( ).
公共部分的体积为:( ).A.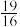 | B.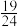 | C.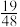 | D.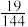 |
您最近一年使用:0次
3 . 如图,已知四面体 的体积为
的体积为 ,
, ,
, 分别为
分别为 ,
, 的中点,
的中点, 、
、 分别在
分别在 、
、 上,且
上,且 、
、 是靠近
是靠近 的三等分点,则多面体
的三等分点,则多面体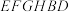 的体积为
的体积为______ .
 的体积为
的体积为 ,
, ,
, 分别为
分别为 ,
, 的中点,
的中点, 、
、 分别在
分别在 、
、 上,且
上,且 、
、 是靠近
是靠近 的三等分点,则多面体
的三等分点,则多面体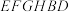 的体积为
的体积为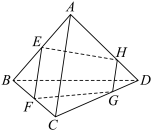
您最近一年使用:0次
4 . 楔体形构件在建筑工程上有广泛的应用.如图,某楔体形构件可视为一个五面体ABCDEF,其中面ABCD为正方形.若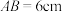 ,
, ,且EF与面ABCD的距离为2cm,则该楔体形构件的体积为
,且EF与面ABCD的距离为2cm,则该楔体形构件的体积为______ .
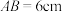 ,
, ,且EF与面ABCD的距离为2cm,则该楔体形构件的体积为
,且EF与面ABCD的距离为2cm,则该楔体形构件的体积为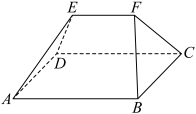
您最近一年使用:0次
5 . 沙漏是古代的一种计时仪器,根据沙子从一个容器漏到另一容器的时间来计时.如图,沙漏可视为上下两个相同的圆锥构成的组合体,下方的容器中装有沙子,沙子堆积成一个圆台,若该沙漏高为6,沙子体积占该沙漏容积的 ,则沙子堆积成的圆台的高( )
,则沙子堆积成的圆台的高( )
 ,则沙子堆积成的圆台的高( )
,则沙子堆积成的圆台的高( )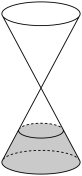
| A.1 | B. | C. | D.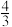 |
您最近一年使用:0次
2024-10-12更新
|
441次组卷
|
4卷引用:广东省部分学校大联考2022-2023学年高三下学期模拟(二)数学试题
名校
解题方法
6 . 如图,一个漏斗形状的几何体上面部分是一个长方体,下面部分是一个四棱锥 ,四棱锥的四条侧棱都相等,两部分的高都是
,四棱锥的四条侧棱都相等,两部分的高都是 ,公共面
,公共面 是一个边长为1的正方形,则( )
是一个边长为1的正方形,则( )
 ,四棱锥的四条侧棱都相等,两部分的高都是
,四棱锥的四条侧棱都相等,两部分的高都是 ,公共面
,公共面 是一个边长为1的正方形,则( )
是一个边长为1的正方形,则( )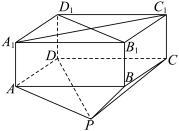
A.该几何体的体积 |
B.直线PD与平面ABCD所成角的正切值为 |
C.异面直线AP与CC1的夹角正弦值为 |
| D.存在一个球,使得该几何体所有顶点都在球面上 |
您最近一年使用:0次
名校
解题方法
7 . 如图所示,一个组合体的上面部分是一个高为0.5 长方体,下面部分是一个正四棱锥,公共面是边长为
长方体,下面部分是一个正四棱锥,公共面是边长为 的正方形,已知该组合体的体积为
的正方形,已知该组合体的体积为 ,则其表面积为( )
,则其表面积为( )
 长方体,下面部分是一个正四棱锥,公共面是边长为
长方体,下面部分是一个正四棱锥,公共面是边长为 的正方形,已知该组合体的体积为
的正方形,已知该组合体的体积为 ,则其表面积为( )
,则其表面积为( )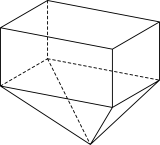
A. | B.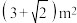 | C. | D.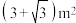 |
您最近一年使用:0次
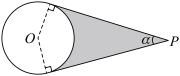
8 . “北斗”卫星系统的全面建成标志着我国的探测领域进入一个新的阶段.单个卫星的探测可简化为如图所示,地球可近似看做圆心为 ,半径
,半径 的球体,
的球体, 为卫星所在位置,阴影部分为观测的空间范围.已知卫星的观测范围为地球表面的可观测区域与
为卫星所在位置,阴影部分为观测的空间范围.已知卫星的观测范围为地球表面的可观测区域与 之间的空间体积
之间的空间体积 (单位:
(单位: ),过
),过 作地球的两条切线,当两切线夹角最大时记为最大观测角
作地球的两条切线,当两切线夹角最大时记为最大观测角 ,可观测地球表面积
,可观测地球表面积 (单位:
(单位: )满足
)满足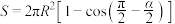 ,则当
,则当 时,
时, ( )
( )
 ,半径
,半径 的球体,
的球体, 为卫星所在位置,阴影部分为观测的空间范围.已知卫星的观测范围为地球表面的可观测区域与
为卫星所在位置,阴影部分为观测的空间范围.已知卫星的观测范围为地球表面的可观测区域与 之间的空间体积
之间的空间体积 (单位:
(单位: ),过
),过 作地球的两条切线,当两切线夹角最大时记为最大观测角
作地球的两条切线,当两切线夹角最大时记为最大观测角 ,可观测地球表面积
,可观测地球表面积 (单位:
(单位: )满足
)满足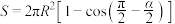 ,则当
,则当 时,
时, ( )
( )
A.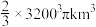 | B.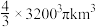 |
C.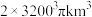 | D.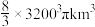 |
您最近一年使用:0次
9 . 图1是边长为1的正六边形 ,将其沿直线
,将其沿直线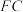 折叠成如图2的空间图形
折叠成如图2的空间图形 ,若
,若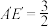 ,则几何体
,则几何体 的体积为( )
的体积为( )
 ,将其沿直线
,将其沿直线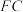 折叠成如图2的空间图形
折叠成如图2的空间图形 ,若
,若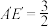 ,则几何体
,则几何体 的体积为( )
的体积为( )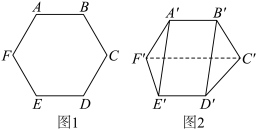
A.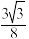 | B. | C.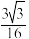 | D. |
您最近一年使用:0次
10 . 某中学开展劳动实习,学习制作模具,有一个模具的毛坏直观图如图所示,它是由一个圆柱体与一个半球对接而成的组合体,已知该几何体的下半部分圆柱的轴截面(过圆柱上、下底面圆的圆心连线的平面) 是面积为16的正方形,则该几何体的体积为( )
是面积为16的正方形,则该几何体的体积为( )
 是面积为16的正方形,则该几何体的体积为( )
是面积为16的正方形,则该几何体的体积为( )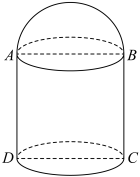
A.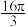 | B. | C.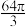 | D. |
您最近一年使用:0次



