名校
解题方法
1 . 如图,已知梯形 中,
中, ,四边形
,四边形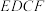 为矩形,
为矩形, ,平面
,平面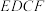 ⊥平面
⊥平面 ,点
,点 是
是 的中点.
的中点.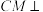 平面
平面 ;
;
(2)求异面直线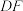 和
和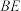 所成角的正弦值.
所成角的正弦值.
(3)求二面角 的余弦值;
的余弦值;
(4)若点 在线段
在线段 上,且直线
上,且直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求线段
,求线段 的长.
的长.
 中,
中, ,四边形
,四边形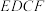 为矩形,
为矩形, ,平面
,平面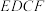 ⊥平面
⊥平面 ,点
,点 是
是 的中点.
的中点.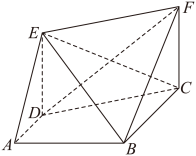
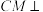 平面
平面 ;
;(2)求异面直线
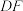 和
和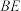 所成角的正弦值.
所成角的正弦值.(3)求二面角
 的余弦值;
的余弦值;(4)若点
 在线段
在线段 上,且直线
上,且直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求线段
,求线段 的长.
的长.
您最近一年使用:0次
名校
解题方法
2 . 如图所示的几何体中,四边形ABCD为矩形,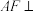 平面
平面 ,
,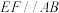 ,
,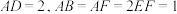 ,点P为棱DF的中点.
,点P为棱DF的中点.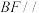 平面APC;
平面APC;
(2)求直线DE与平面BCF所成角的正弦值;
(3)求平面ACP与平面BCF的夹角的余弦值:
(4)求点F到平面ACP的距离.
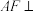 平面
平面 ,
,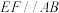 ,
,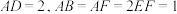 ,点P为棱DF的中点.
,点P为棱DF的中点.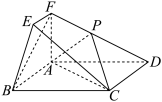
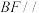 平面APC;
平面APC;(2)求直线DE与平面BCF所成角的正弦值;
(3)求平面ACP与平面BCF的夹角的余弦值:
(4)求点F到平面ACP的距离.
您最近一年使用:0次
名校
解题方法
3 . 在空间直角坐标系 中,已知向量
中,已知向量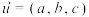 ,点
,点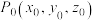 .若直线
.若直线 以
以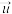 为方向向量且经过点
为方向向量且经过点 ,则直线
,则直线 的标准式方程可表示为
的标准式方程可表示为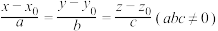 ;若平面
;若平面 以
以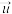 为法向量且经过点
为法向量且经过点 ,则平面
,则平面 的点法式方程表示为
的点法式方程表示为 .
.
(1)已知直线 的标准式方程为
的标准式方程为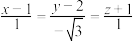 ,平面
,平面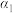 的点法式方程可表示为
的点法式方程可表示为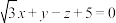 ,求直线
,求直线 与平面
与平面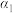 所成角的余弦值;
所成角的余弦值;
(2)已知平面 的点法式方程可表示为
的点法式方程可表示为 ,平面外一点
,平面外一点 ,求点
,求点 到平面
到平面 的距离;
的距离;
(3)(i)若集合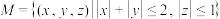 ,记集合
,记集合 中所有点构成的几何体为
中所有点构成的几何体为 ,求几何体
,求几何体 的体积:
的体积:
(ii)若集合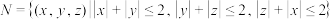 .记集合
.记集合 中所有点构成的几何体为
中所有点构成的几何体为 ,求几何体
,求几何体 相邻两个面(有公共棱)所成二面角的大小
相邻两个面(有公共棱)所成二面角的大小
 中,已知向量
中,已知向量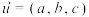 ,点
,点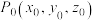 .若直线
.若直线 以
以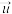 为方向向量且经过点
为方向向量且经过点 ,则直线
,则直线 的标准式方程可表示为
的标准式方程可表示为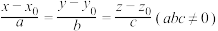 ;若平面
;若平面 以
以 为法向量且经过点
为法向量且经过点 ,则平面
,则平面 的点法式方程表示为
的点法式方程表示为 .
.(1)已知直线
 的标准式方程为
的标准式方程为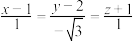 ,平面
,平面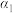 的点法式方程可表示为
的点法式方程可表示为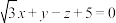 ,求直线
,求直线 与平面
与平面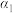 所成角的余弦值;
所成角的余弦值;(2)已知平面
 的点法式方程可表示为
的点法式方程可表示为 ,平面外一点
,平面外一点 ,求点
,求点 到平面
到平面 的距离;
的距离;(3)(i)若集合
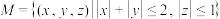 ,记集合
,记集合 中所有点构成的几何体为
中所有点构成的几何体为 ,求几何体
,求几何体 的体积:
的体积:(ii)若集合
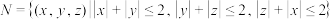 .记集合
.记集合 中所有点构成的几何体为
中所有点构成的几何体为 ,求几何体
,求几何体 相邻两个面(有公共棱)所成二面角的大小
相邻两个面(有公共棱)所成二面角的大小
您最近一年使用:0次
今日更新
|
106次组卷
|
2卷引用:湖南省长沙市明德中学2024-2025学年高二上学期10月阶段检测数学试卷
名校
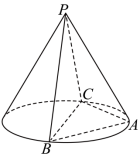
4 . 如图, 、
、 、
、 为圆锥三条母线,
为圆锥三条母线, .
.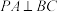 ;
;
(2)若圆锥侧面积为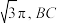 为底面直径,
为底面直径, ,求平面
,求平面 和平面
和平面 所成角的余弦值.
所成角的余弦值.
 、
、 、
、 为圆锥三条母线,
为圆锥三条母线, .
.
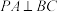 ;
;(2)若圆锥侧面积为
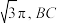 为底面直径,
为底面直径, ,求平面
,求平面 和平面
和平面 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
5 . 如图,在四棱锥 中,底面ABCD为菱形,
中,底面ABCD为菱形,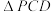 是边长为2的正三角形,
是边长为2的正三角形,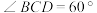 ,平面
,平面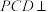 平面ABCD.
平面ABCD.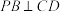 ;
;
(2)直线PB与平面APD所成角的正弦值;
(3)求平面APD与平面PCD夹角的余弦值.
 中,底面ABCD为菱形,
中,底面ABCD为菱形,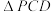 是边长为2的正三角形,
是边长为2的正三角形,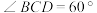 ,平面
,平面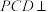 平面ABCD.
平面ABCD.
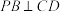 ;
;(2)直线PB与平面APD所成角的正弦值;
(3)求平面APD与平面PCD夹角的余弦值.
您最近一年使用:0次
解题方法
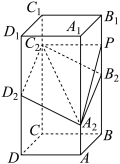
6 . 如图,在正四棱柱 中,
中, ,
,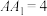 ,点
,点 ,
, ,
, ,
, 分别在棱
分别在棱 ,
, ,
, ,
, 上,
上,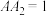 ,
,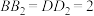 ,
,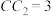 .
. ,
, ,
, ,
, 四点共面;
四点共面;
(2)在棱 上是否存在点
上是否存在点 ,使得平面
,使得平面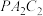 与平面
与平面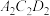 的夹角为
的夹角为 ,若不存在,请说明理由;若存在求
,若不存在,请说明理由;若存在求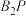 的长.
的长.
(3)若 为棱
为棱 上一点,当
上一点,当 为何值时,平面
为何值时,平面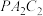 与平面
与平面 的夹角的正弦值最小?
的夹角的正弦值最小?
 中,
中, ,
,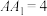 ,点
,点 ,
, ,
, ,
, 分别在棱
分别在棱 ,
, ,
, ,
, 上,
上,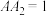 ,
,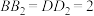 ,
,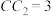 .
.
 ,
, ,
, ,
, 四点共面;
四点共面;(2)在棱
 上是否存在点
上是否存在点 ,使得平面
,使得平面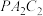 与平面
与平面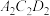 的夹角为
的夹角为 ,若不存在,请说明理由;若存在求
,若不存在,请说明理由;若存在求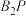 的长.
的长.(3)若
 为棱
为棱 上一点,当
上一点,当 为何值时,平面
为何值时,平面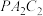 与平面
与平面 的夹角的正弦值最小?
的夹角的正弦值最小?
您最近一年使用:0次
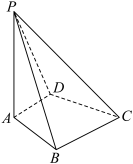
7 . 如图,在四棱锥 中,
中, 底面
底面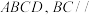 平面
平面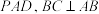 .
. 平面PAB.
平面PAB.
(2)若 ,
, ,且异面直线PD与BC所成角的正切值为
,且异面直线PD与BC所成角的正切值为 ,求平面PAB与平面PCD所成二面角的正弦值.
,求平面PAB与平面PCD所成二面角的正弦值.
 中,
中, 底面
底面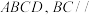 平面
平面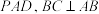 .
.
 平面PAB.
平面PAB.(2)若
 ,
, ,且异面直线PD与BC所成角的正切值为
,且异面直线PD与BC所成角的正切值为 ,求平面PAB与平面PCD所成二面角的正弦值.
,求平面PAB与平面PCD所成二面角的正弦值.
您最近一年使用:0次
今日更新
|
215次组卷
|
2卷引用:江西省多校2024-2025学年高三上学期10月联考数学试题
解题方法
8 . 如图,在六面体 中,
中, ,且底面
,且底面 为菱形.
为菱形. 为平行四边形.
为平行四边形.
(2)若 平面
平面 ,求平面
,求平面 与平面
与平面 所成二面角的正弦值.
所成二面角的正弦值.
 中,
中, ,且底面
,且底面 为菱形.
为菱形.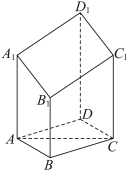
 为平行四边形.
为平行四边形.(2)若
 平面
平面 ,求平面
,求平面 与平面
与平面 所成二面角的正弦值.
所成二面角的正弦值.
您最近一年使用:0次
9 . 如图1,在边长为4的菱形 中,
中,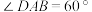 ,点M,N分别是边
,点M,N分别是边 ,
, 的中点,
的中点, ,
,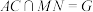 .沿
.沿 将
将 翻折到
翻折到 的位置,连接
的位置,连接 ,
, ,
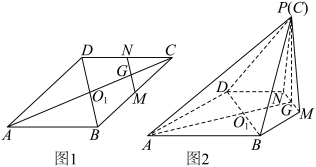
, ,得到如图2 所示的五棱锥
,得到如图2 所示的五棱锥 .
. 平面
平面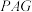 ?证明你的结论;
?证明你的结论;
(2)若平面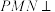 平面
平面 ,线段
,线段 上是否存在一点Q,使得平面
上是否存在一点Q,使得平面 与平面
与平面 所成角的余弦值为
所成角的余弦值为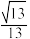 ?若存在,试确定点Q的位置;若不存在,请说明理由.
?若存在,试确定点Q的位置;若不存在,请说明理由.
 中,
中,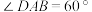 ,点M,N分别是边
,点M,N分别是边 ,
, 的中点,
的中点, ,
,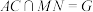 .沿
.沿 将
将 翻折到
翻折到 的位置,连接
的位置,连接 ,
, ,
, ,得到如图2 所示的五棱锥
,得到如图2 所示的五棱锥 .
.
 平面
平面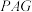 ?证明你的结论;
?证明你的结论;(2)若平面
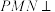 平面
平面 ,线段
,线段 上是否存在一点Q,使得平面
上是否存在一点Q,使得平面 与平面
与平面 所成角的余弦值为
所成角的余弦值为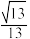 ?若存在,试确定点Q的位置;若不存在,请说明理由.
?若存在,试确定点Q的位置;若不存在,请说明理由.
您最近一年使用:0次
昨日更新
|
636次组卷
|
4卷引用:福建省厦门双十中学2022-2023学年高二上学期第二次月考数学试题
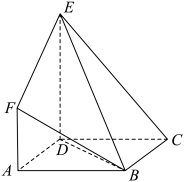
10 . 如图,在多面体 中,梯形
中,梯形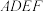 与平行四边形
与平行四边形 所在平面互相垂直,
所在平面互相垂直,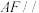
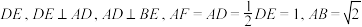 .
. ;
;
(2)求二面角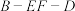 的余弦值;
的余弦值;
(3)判断线段 上是否存在点
上是否存在点 ,使得平面
,使得平面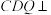 平面
平面 ?若存在,求出
?若存在,求出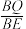 的值,若不存在,说明理由.
的值,若不存在,说明理由.
 中,梯形
中,梯形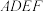 与平行四边形
与平行四边形 所在平面互相垂直,
所在平面互相垂直,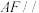
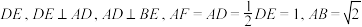 .
.
 ;
;(2)求二面角
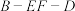 的余弦值;
的余弦值;(3)判断线段
 上是否存在点
上是否存在点 ,使得平面
,使得平面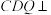 平面
平面 ?若存在,求出
?若存在,求出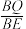 的值,若不存在,说明理由.
的值,若不存在,说明理由.
您最近一年使用:0次



