2024高三下·全国·专题练习
解题方法
1 . 如图1,矩形 中,
中, ,将三角形
,将三角形 沿着线段
沿着线段 翻折,正方形
翻折,正方形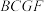 沿着
沿着 翻折,使得
翻折,使得 与
与 重合,
重合, 与
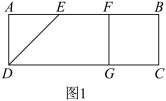
与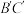 重合,得到如图2所示的几何体,其中
重合,得到如图2所示的几何体,其中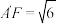 ,平面
,平面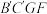 ⊥平面
⊥平面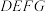 ,点
,点 为线段
为线段 的中点,点
的中点,点 在线段
在线段 上,且
上,且 .
.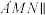 平面
平面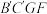 ;
;
(2)求二面角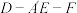 的正弦值.
的正弦值.
 中,
中, ,将三角形
,将三角形 沿着线段
沿着线段 翻折,正方形
翻折,正方形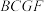 沿着
沿着 翻折,使得
翻折,使得 与
与 重合,
重合, 与
与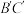 重合,得到如图2所示的几何体,其中
重合,得到如图2所示的几何体,其中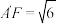 ,平面
,平面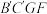 ⊥平面
⊥平面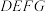 ,点
,点 为线段
为线段 的中点,点
的中点,点 在线段
在线段 上,且
上,且 .
.
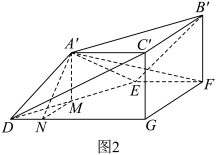
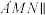 平面
平面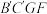 ;
;(2)求二面角
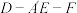 的正弦值.
的正弦值.
您最近半年使用:0次
名校
解题方法
2 . 如图,在边长为 的正方体
的正方体 中,
中, 为
为 中点,
中点,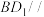 平面
平面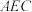 ;
;
(2)求三棱锥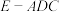 的体积.
的体积.
 的正方体
的正方体 中,
中, 为
为 中点,
中点,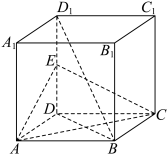
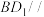 平面
平面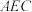 ;
;(2)求三棱锥
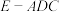 的体积.
的体积.
您最近半年使用:0次
解题方法
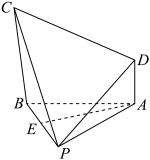
3 . 如图,在四棱锥 中,
中,
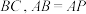 ,平面
,平面 平面
平面 ,平面
,平面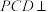 平面
平面 .
. 是
是 的中点,求证:
的中点,求证: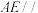 平面
平面 ;
;
(2)若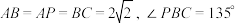 ,求三棱锥
,求三棱锥 体积的最大值.
体积的最大值.
 中,
中,
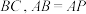 ,平面
,平面 平面
平面 ,平面
,平面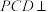 平面
平面 .
.
 是
是 的中点,求证:
的中点,求证: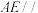 平面
平面 ;
;(2)若
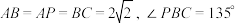 ,求三棱锥
,求三棱锥 体积的最大值.
体积的最大值.
您最近半年使用:0次
名校
解题方法
4 . 在如图所示的多面体中, 平面
平面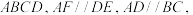
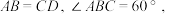

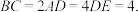
 上求作点
上求作点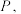 使
使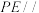 平面
平面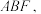 请写出作法并说明理由;
请写出作法并说明理由;
(2)求三棱锥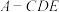 的高.
的高.
 平面
平面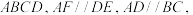
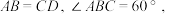

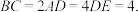
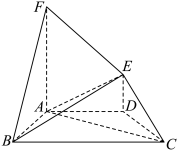
 上求作点
上求作点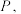 使
使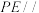 平面
平面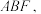 请写出作法并说明理由;
请写出作法并说明理由;(2)求三棱锥
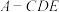 的高.
的高.
您最近半年使用:0次
5 . 如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形, 平面
平面 ,
, 为
为 的中点.
的中点. 与直线
与直线 相交于点
相交于点 ,求证:
,求证: ;
;
(2)若 ,
,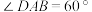 ,
,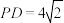 ,求直线
,求直线 与平面
与平面 所成角的大小.
所成角的大小.
 中,底面
中,底面 为菱形,
为菱形, 平面
平面 ,
, 为
为 的中点.
的中点.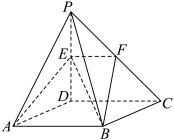
 与直线
与直线 相交于点
相交于点 ,求证:
,求证: ;
;(2)若
 ,
,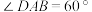 ,
, ,求直线
,求直线 与平面
与平面 所成角的大小.
所成角的大小.
您最近半年使用:0次
解题方法
6 . 如图,在四棱锥 中,底面
中,底面 是边长为1的正方形,
是边长为1的正方形,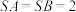 ,
, 、
、 分别是
分别是 、
、 的中点.
的中点.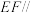 平面
平面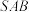 ;
;
(2)若二面角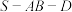 的大小为
的大小为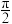 ,求直线
,求直线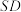 与平面
与平面 所成角的大小.
所成角的大小.
 中,底面
中,底面 是边长为1的正方形,
是边长为1的正方形,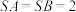 ,
, 、
、 分别是
分别是 、
、 的中点.
的中点.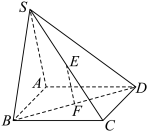
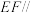 平面
平面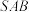 ;
;(2)若二面角
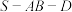 的大小为
的大小为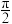 ,求直线
,求直线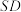 与平面
与平面 所成角的大小.
所成角的大小.
您最近半年使用:0次
名校
7 . 如图,三棱柱 中,面
中,面 面
面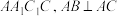 ,
, ,
, .过
.过 的平面交线段
的平面交线段 于点
于点 (不与端点重合),交线段
(不与端点重合),交线段 于点
于点 .
.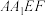 为平行四边形;
为平行四边形;
(2)若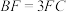 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,面
中,面 面
面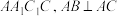 ,
, ,
, .过
.过 的平面交线段
的平面交线段 于点
于点 (不与端点重合),交线段
(不与端点重合),交线段 于点
于点 .
.
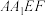 为平行四边形;
为平行四边形;(2)若
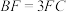 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近半年使用:0次
名校
解题方法
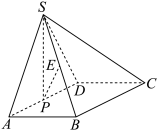
8 . 如图,在四棱锥 中,四边形
中,四边形 是矩形,
是矩形, 是正三角形,且平面
是正三角形,且平面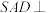 平面
平面 ,
, ,
, 为棱
为棱 的中点,四棱锥
的中点,四棱锥 的体积为
的体积为 .
. 为棱
为棱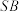 的中点,求证:
的中点,求证: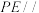 平面
平面 ;
;
(2)在棱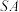 上是否存在点
上是否存在点 ,使得平面
,使得平面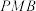 与平面
与平面 所成夹角的余弦值为
所成夹角的余弦值为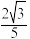 ?若存在,求出线段
?若存在,求出线段 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
 中,四边形
中,四边形 是矩形,
是矩形, 是正三角形,且平面
是正三角形,且平面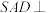 平面
平面 ,
, ,
, 为棱
为棱 的中点,四棱锥
的中点,四棱锥 的体积为
的体积为 .
.
 为棱
为棱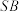 的中点,求证:
的中点,求证: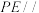 平面
平面 ;
;(2)在棱
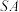 上是否存在点
上是否存在点 ,使得平面
,使得平面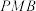 与平面
与平面 所成夹角的余弦值为
所成夹角的余弦值为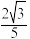 ?若存在,求出线段
?若存在,求出线段 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
您最近半年使用:0次
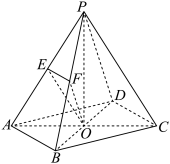
9 . 如图,在四棱锥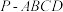 中,底面
中,底面 是矩形,
是矩形, ,
, ,
,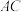 与
与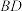 交于点O,
交于点O,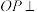 底面
底面 ,
,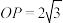 ,点E,F分别是棱
,点E,F分别是棱 ,
,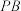 的中点,连接
的中点,连接 ,
,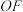 ,
,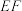 .
.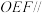 平面
平面 ;
;
(2)求二面角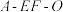 的余弦值.
的余弦值.
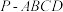 中,底面
中,底面 是矩形,
是矩形, ,
, ,
,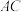 与
与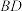 交于点O,
交于点O,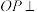 底面
底面 ,
,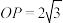 ,点E,F分别是棱
,点E,F分别是棱 ,
,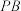 的中点,连接
的中点,连接 ,
,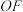 ,
,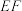 .
.
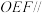 平面
平面 ;
;(2)求二面角
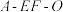 的余弦值.
的余弦值.
您最近半年使用:0次
解题方法
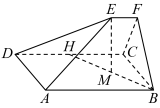
10 . 如图,在五面体 中,底面
中,底面 为正方形,
为正方形,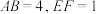 .
.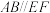 ;
;
(2)若 为
为 的中点,
的中点, 为
为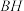 的中点,
的中点,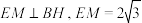 ,再从条件①、条件②这两个条件中选择一个作为已知,求直线
,再从条件①、条件②这两个条件中选择一个作为已知,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
条件①: ;
;
条件②: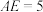 .
.
注:如果选择条件①和条件②分别解答,按第一个解答计分
 中,底面
中,底面 为正方形,
为正方形,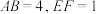 .
.
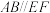 ;
;(2)若
 为
为 的中点,
的中点, 为
为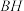 的中点,
的中点,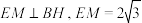 ,再从条件①、条件②这两个条件中选择一个作为已知,求直线
,再从条件①、条件②这两个条件中选择一个作为已知,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.条件①:
 ;
;条件②:
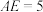 .
.注:如果选择条件①和条件②分别解答,按第一个解答计分
您最近半年使用:0次



