解题方法
1 . 已知正方形ABCD的顶点均在表面积为 的球O的球面上,则当四棱锥
的球O的球面上,则当四棱锥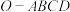 的体积取得最大值时,点O到平面ABCD的距离为( )
的体积取得最大值时,点O到平面ABCD的距离为( )
 的球O的球面上,则当四棱锥
的球O的球面上,则当四棱锥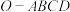 的体积取得最大值时,点O到平面ABCD的距离为( )
的体积取得最大值时,点O到平面ABCD的距离为( )A. | B. | C. | D.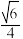 |
您最近一年使用:0次
今日更新
|
3次组卷
|
2卷引用:陕西省铜川市王益中学2024届高三下学期高考猜题信息卷(二)文科数学试题
解题方法
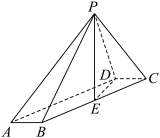
2 . 如图,在四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形,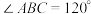 ,
, ,
,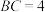 ,
, ,
,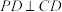 ,点E是
,点E是 的中点,且
的中点,且 .
. ;
;
(2)求点E到平面 的距离.
的距离.
 中,底面
中,底面 是平行四边形,
是平行四边形,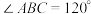 ,
, ,
,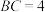 ,
, ,
,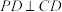 ,点E是
,点E是 的中点,且
的中点,且 .
.
 ;
;(2)求点E到平面
 的距离.
的距离.
您最近一年使用:0次
解题方法
3 . 如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径 相等,则下列结论正确的是( )
相等,则下列结论正确的是( )
 相等,则下列结论正确的是( )
相等,则下列结论正确的是( )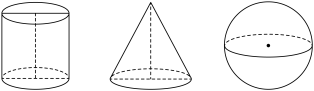
A.圆柱的侧面积为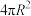 |
B.圆锥的侧面积为 |
| C.圆柱的侧面积与球的表面积相等 |
D.圆柱、圆锥、球的体积之比为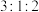 |
您最近一年使用:0次
解题方法
4 . 如图,在棱长为1的正方体 中,点
中,点 ,
, ,
, 分别是棱
分别是棱 ,
, ,
, 的中点,
的中点, 为线段
为线段 上的一个动点,平面
上的一个动点,平面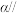 平面
平面 ,则下列说法中正确的是( )
,则下列说法中正确的是( )
 中,点
中,点 ,
, ,
, 分别是棱
分别是棱 ,
, ,
, 的中点,
的中点, 为线段
为线段 上的一个动点,平面
上的一个动点,平面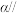 平面
平面 ,则下列说法中正确的是( )
,则下列说法中正确的是( )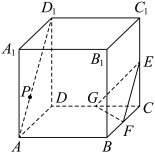
A.不存在点 ,使得 ,使得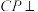 平面 平面 |
B.三棱锥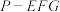 的体积为定值 的体积为定值 |
C.平面 截该正方体所得截面的面积的最大值为 截该正方体所得截面的面积的最大值为 |
D.平面 截该正方体所得截面可能是三角形或六边形 截该正方体所得截面可能是三角形或六边形 |
您最近一年使用:0次
解题方法
5 . 如图,在棱长为4的正方体 中,将侧面
中,将侧面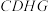 沿
沿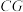 逆时针旋转角度
逆时针旋转角度 至平面
至平面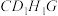 ,其中
,其中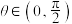 ,点
,点 是线段
是线段 的中点.
的中点.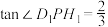 时,求四棱锥
时,求四棱锥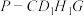 的体积;
的体积;
(2)当直线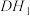 与平面
与平面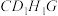 所成的角为
所成的角为 时,求
时,求 的值.
的值.
 中,将侧面
中,将侧面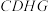 沿
沿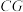 逆时针旋转角度
逆时针旋转角度 至平面
至平面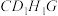 ,其中
,其中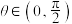 ,点
,点 是线段
是线段 的中点.
的中点.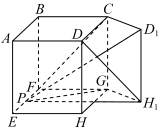
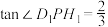 时,求四棱锥
时,求四棱锥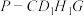 的体积;
的体积;(2)当直线
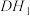 与平面
与平面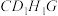 所成的角为
所成的角为 时,求
时,求 的值.
的值.
您最近一年使用:0次
解题方法
6 . 在三棱锥 中,
中, ,
, ,△
,△ 是正三角形,
是正三角形,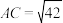 ,则三棱锥
,则三棱锥 的体积为
的体积为______ ;此三棱锥外接球的表面积为______ .
 中,
中, ,
, ,△
,△ 是正三角形,
是正三角形,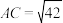 ,则三棱锥
,则三棱锥 的体积为
的体积为
您最近一年使用:0次
解题方法
7 . 已知 ,
, ,
, 为球
为球 的球面上的三个点,若
的球面上的三个点,若 ,
, ,球
,球 的表面积为
的表面积为 ,则三棱锥
,则三棱锥 的体积的最大值为
的体积的最大值为___________ .
 ,
, ,
, 为球
为球 的球面上的三个点,若
的球面上的三个点,若 ,
, ,球
,球 的表面积为
的表面积为 ,则三棱锥
,则三棱锥 的体积的最大值为
的体积的最大值为
您最近一年使用:0次
8 . 在棱长为1的正方体 中,点M在线段
中,点M在线段 上运动(包含端点),则( )
上运动(包含端点),则( )
 中,点M在线段
中,点M在线段 上运动(包含端点),则( )
上运动(包含端点),则( )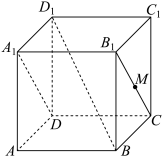
A.直线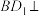 平面 平面 |
B.正方体 外接球的表面积为 外接球的表面积为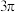 |
C.三棱锥 的体积为定值 的体积为定值 |
D.直线AM与平面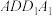 的夹角可能为 的夹角可能为 |
您最近一年使用:0次
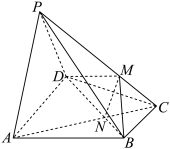
9 . 如图,在四棱锥 中,底面
中,底面 为等腰梯形,
为等腰梯形,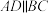 ,
, ,
, 为
为 与
与 的交点,
的交点, 为
为 上一点,且
上一点,且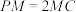 .
. 平面
平面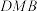 ;
;
(2)若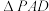 为正三角形,
为正三角形, ,求异面直线
,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)若点 到底面
到底面 的距离为3,求三棱锥
的距离为3,求三棱锥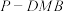 的体积.
的体积.
 中,底面
中,底面 为等腰梯形,
为等腰梯形,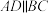 ,
, ,
, 为
为 与
与 的交点,
的交点, 为
为 上一点,且
上一点,且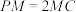 .
.
 平面
平面 ;
;(2)若
 为正三角形,
为正三角形, ,求异面直线
,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;(3)若点
 到底面
到底面 的距离为3,求三棱锥
的距离为3,求三棱锥 的体积.
的体积.
您最近一年使用:0次



