名校
解题方法
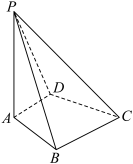
1 . 如图,已知梯形 中,
中, ,四边形
,四边形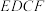 为矩形,
为矩形, ,平面
,平面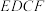 ⊥平面
⊥平面 ,点
,点 是
是 的中点.
的中点.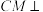 平面
平面 ;
;
(2)求异面直线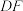 和
和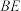 所成角的正弦值.
所成角的正弦值.
(3)求二面角 的余弦值;
的余弦值;
(4)若点 在线段
在线段 上,且直线
上,且直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求线段
,求线段 的长.
的长.
 中,
中, ,四边形
,四边形 为矩形,
为矩形, ,平面
,平面 ⊥平面
⊥平面 ,点
,点 是
是 的中点.
的中点.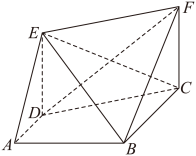
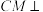 平面
平面 ;
;(2)求异面直线
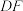 和
和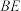 所成角的正弦值.
所成角的正弦值.(3)求二面角
 的余弦值;
的余弦值;(4)若点
 在线段
在线段 上,且直线
上,且直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求线段
,求线段 的长.
的长.
您最近一年使用:0次
2 . 如图,在四棱锥 中,底面ABCD为菱形,
中,底面ABCD为菱形,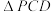 是边长为2的正三角形,
是边长为2的正三角形,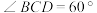 ,平面
,平面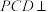 平面ABCD.
平面ABCD.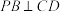 ;
;
(2)直线PB与平面APD所成角的正弦值;
(3)求平面APD与平面PCD夹角的余弦值.
 中,底面ABCD为菱形,
中,底面ABCD为菱形,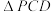 是边长为2的正三角形,
是边长为2的正三角形,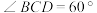 ,平面
,平面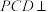 平面ABCD.
平面ABCD.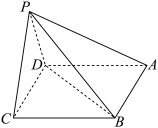
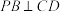 ;
;(2)直线PB与平面APD所成角的正弦值;
(3)求平面APD与平面PCD夹角的余弦值.
您最近一年使用:0次
3 . 如图,在四棱锥 中,
中, 底面
底面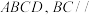 平面
平面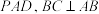 .
. 平面PAB.
平面PAB.
(2)若 ,
, ,且异面直线PD与BC所成角的正切值为
,且异面直线PD与BC所成角的正切值为 ,求平面PAB与平面PCD所成二面角的正弦值.
,求平面PAB与平面PCD所成二面角的正弦值.
 中,
中, 底面
底面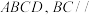 平面
平面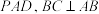 .
.
 平面PAB.
平面PAB.(2)若
 ,
, ,且异面直线PD与BC所成角的正切值为
,且异面直线PD与BC所成角的正切值为 ,求平面PAB与平面PCD所成二面角的正弦值.
,求平面PAB与平面PCD所成二面角的正弦值.
您最近一年使用:0次
今日更新
|
215次组卷
|
2卷引用:江西省多校2024-2025学年高三上学期10月联考数学试题
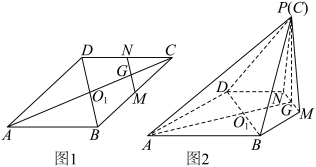
4 . 如图1,在边长为4的菱形 中,
中,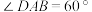 ,点M,N分别是边
,点M,N分别是边 ,
, 的中点,
的中点, ,
,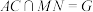 .沿
.沿 将
将 翻折到
翻折到 的位置,连接
的位置,连接 ,
, ,
, ,得到如图2 所示的五棱锥
,得到如图2 所示的五棱锥 .
. 平面
平面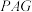 ?证明你的结论;
?证明你的结论;
(2)若平面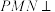 平面
平面 ,线段
,线段 上是否存在一点Q,使得平面
上是否存在一点Q,使得平面 与平面
与平面 所成角的余弦值为
所成角的余弦值为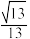 ?若存在,试确定点Q的位置;若不存在,请说明理由.
?若存在,试确定点Q的位置;若不存在,请说明理由.
 中,
中,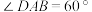 ,点M,N分别是边
,点M,N分别是边 ,
, 的中点,
的中点, ,
,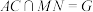 .沿
.沿 将
将 翻折到
翻折到 的位置,连接
的位置,连接 ,
, ,
, ,得到如图2 所示的五棱锥
,得到如图2 所示的五棱锥 .
.
 平面
平面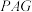 ?证明你的结论;
?证明你的结论;(2)若平面
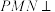 平面
平面 ,线段
,线段 上是否存在一点Q,使得平面
上是否存在一点Q,使得平面 与平面
与平面 所成角的余弦值为
所成角的余弦值为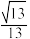 ?若存在,试确定点Q的位置;若不存在,请说明理由.
?若存在,试确定点Q的位置;若不存在,请说明理由.
您最近一年使用:0次
昨日更新
|
636次组卷
|
4卷引用:福建省厦门双十中学2022-2023学年高二上学期第二次月考数学试题
名校
5 . 在三棱柱 中,平面
中,平面 平面
平面 ,
, ,
,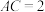 ,
,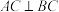 ,
, .
.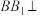 平面
平面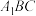 ;
;
(2)若异面直线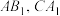 所成角的余弦值为
所成角的余弦值为 ,求BC.
,求BC.
 中,平面
中,平面 平面
平面 ,
, ,
,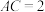 ,
,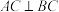 ,
, .
.
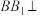 平面
平面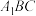 ;
;(2)若异面直线
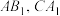 所成角的余弦值为
所成角的余弦值为 ,求BC.
,求BC.
您最近一年使用:0次
昨日更新
|
300次组卷
|
3卷引用:河北省邢台市临西县翰林中学等校2024-2025学年高二上学期第一次月考数学试题
名校
解题方法
6 . 如图,在棱长为2的正方体 中,
中, 为棱
为棱 的中点,
的中点, 为棱
为棱 上一点.请用向量方法解决以下问题:
上一点.请用向量方法解决以下问题: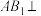 平面
平面 ;
;
(2)是否存在点 ,使直线
,使直线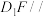 平面
平面 ?若存在,求出
?若存在,求出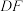 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
 中,
中, 为棱
为棱 的中点,
的中点, 为棱
为棱 上一点.请用向量方法解决以下问题:
上一点.请用向量方法解决以下问题: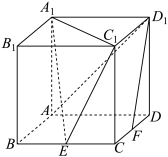
 平面
平面 ;
;(2)是否存在点
 ,使直线
,使直线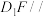 平面
平面 ?若存在,求出
?若存在,求出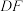 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
您最近一年使用:0次
2024高二上·全国·专题练习
解题方法
7 . 如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,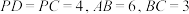 .点E是
.点E是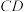 边的中点.点F,G分别在线段
边的中点.点F,G分别在线段 ,BC上,且
,BC上,且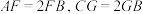 .求直线
.求直线 与直线
与直线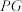 所成角的余弦值.
所成角的余弦值.
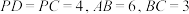 .点E是
.点E是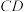 边的中点.点F,G分别在线段
边的中点.点F,G分别在线段 ,BC上,且
,BC上,且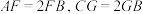 .求直线
.求直线 与直线
与直线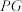 所成角的余弦值.
所成角的余弦值.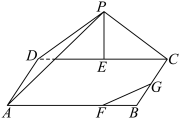
您最近一年使用:0次
名校
解题方法
8 . 如图,在四棱锥 中,底面
中,底面 为矩形且
为矩形且 ,侧面
,侧面 底面
底面 ,且侧面
,且侧面 是正三角形,
是正三角形, 、
、 分别是
分别是 ,
, 的中点.
的中点.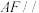 平面
平面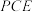 ;
;
(2)求直线 与平面
与平面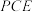 所成角的余弦值.
所成角的余弦值.
 中,底面
中,底面 为矩形且
为矩形且 ,侧面
,侧面 底面
底面 ,且侧面
,且侧面 是正三角形,
是正三角形, 、
、 分别是
分别是 ,
, 的中点.
的中点.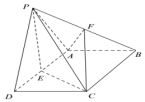
 平面
平面 ;
;(2)求直线
 与平面
与平面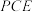 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
2024高二上·全国·专题练习
解题方法
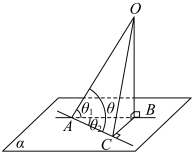
9 . 如图,A为平面 上一点,过A的斜线
上一点,过A的斜线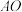 在平面
在平面 上的射影为
上的射影为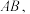
 为平面
为平面 上的一条直线,证明:
上的一条直线,证明: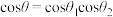 .
.
 上一点,过A的斜线
上一点,过A的斜线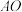 在平面
在平面 上的射影为
上的射影为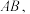
 为平面
为平面 上的一条直线,证明:
上的一条直线,证明: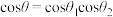 .
.
您最近一年使用:0次
名校
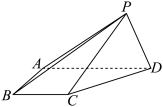
10 . 如图,在四棱锥 中,
中, ,
, ,
, ,
, ,
, 平面
平面 .
. 平面
平面 ;
;
(2)求 的长;
的长;
(3)若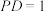 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, ,
, ,
, ,
, ,
, 平面
平面 .
.
 平面
平面 ;
;(2)求
 的长;
的长;(3)若
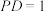 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
昨日更新
|
371次组卷
|
2卷引用:湖南省常德市临澧县第一中学2025届高三上学期第二次阶段性考试数学试题



