名校
解题方法
1 . 2021年3月1日,国务院新闻办公室举行新闻发布会,工业和信息化部长肖亚庆先生提出了芯片发展的五项措施,进一步激励国内科技巨头加大了科技研发投入的力度.中华技术有限公司拟对“麒麟”手机芯片进行科技升级,根据市场调研与模拟,得到科技升级投入 (亿元)与科技升级直接纯收益
(亿元)与科技升级直接纯收益 (亿元)的数据统计如下:
(亿元)的数据统计如下:
当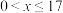 时,建立了
时,建立了 与
与 的两个回归模型:模型①:
的两个回归模型:模型①: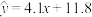 ;模型②:
;模型②: ;当
;当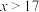 时,确定
时,确定 与
与 满足的线性回归方程为
满足的线性回归方程为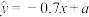 .
.
(1)根据下列表格中的数据,比较当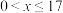 时模型①、②的相关指数
时模型①、②的相关指数 的大小,并选择拟合精度更高、更可靠的模型.
的大小,并选择拟合精度更高、更可靠的模型.
(附:刻画回归效果的相关指数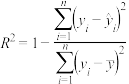 ,
, )
)
(2)为鼓励科技创新,当科技升级的投入不少于20亿元时,国家给予公司补贴5亿元,以回归方程为预测依据,应用(1)的结论,比较科技升级投入17亿元与20亿元时公司实际收益的大小.
(附:线性回归方程 的系数关系:
的系数关系: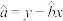 )
)
(3)科技升级后,“麒麟”芯片的效率 大幅提高,经实际试验得
大幅提高,经实际试验得 大致服从正态分布
大致服从正态分布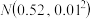 .公司对科技升级团队的奖励方案如下:若芯片的效率不超过
.公司对科技升级团队的奖励方案如下:若芯片的效率不超过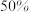 ,不予奖励:若芯片的效率超过
,不予奖励:若芯片的效率超过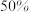 ,但不超过
,但不超过 ,每部芯片奖励2元;若芯片的效率超过
,每部芯片奖励2元;若芯片的效率超过 ,每部芯片奖励4元.记
,每部芯片奖励4元.记 为每部芯片获得的奖励,求
为每部芯片获得的奖励,求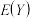 (精确到0.01).
(精确到0.01).
(附:若随机变量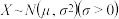 ,则
,则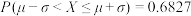 ,
,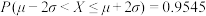 )
)
 (亿元)与科技升级直接纯收益
(亿元)与科技升级直接纯收益 (亿元)的数据统计如下:
(亿元)的数据统计如下:序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 | 3 | 4 | 6 | 8 | 10 | 13 | 21 | 22 | 23 | 24 | 25 |
| 13 | 22 | 31 | 42 | 50 | 56 | 58 | 68.5 | 68 | 67.5 | 66 | 66 |
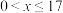 时,建立了
时,建立了 与
与 的两个回归模型:模型①:
的两个回归模型:模型①: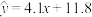 ;模型②:
;模型②: ;当
;当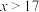 时,确定
时,确定 与
与 满足的线性回归方程为
满足的线性回归方程为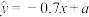 .
.(1)根据下列表格中的数据,比较当
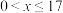 时模型①、②的相关指数
时模型①、②的相关指数 的大小,并选择拟合精度更高、更可靠的模型.
的大小,并选择拟合精度更高、更可靠的模型.回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 182.4 | 79.2 |
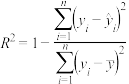 ,
, )
)(2)为鼓励科技创新,当科技升级的投入不少于20亿元时,国家给予公司补贴5亿元,以回归方程为预测依据,应用(1)的结论,比较科技升级投入17亿元与20亿元时公司实际收益的大小.
(附:线性回归方程
 的系数关系:
的系数关系: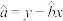 )
)(3)科技升级后,“麒麟”芯片的效率
 大幅提高,经实际试验得
大幅提高,经实际试验得 大致服从正态分布
大致服从正态分布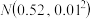 .公司对科技升级团队的奖励方案如下:若芯片的效率不超过
.公司对科技升级团队的奖励方案如下:若芯片的效率不超过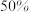 ,不予奖励:若芯片的效率超过
,不予奖励:若芯片的效率超过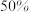 ,但不超过
,但不超过 ,每部芯片奖励2元;若芯片的效率超过
,每部芯片奖励2元;若芯片的效率超过 ,每部芯片奖励4元.记
,每部芯片奖励4元.记 为每部芯片获得的奖励,求
为每部芯片获得的奖励,求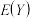 (精确到0.01).
(精确到0.01).(附:若随机变量
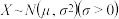 ,则
,则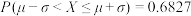 ,
,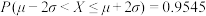 )
)
您最近一年使用:0次
2021-08-23更新
|
668次组卷
|
3卷引用:重庆市南开中学校2023届高三上学期期末数学试题
名校
2 . 今年九月,九龙坡区创建全国文明城区活动正式启动,中央文明办对九龙坡辖区内的市民进行了创建文明城区相关知识(文明城区宣传、建党100周年、社会主义核心价值观、红色基因教育等)网络问卷调查,每一位市民只有一次答题机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,绘制成如下的频率分布直方图

(1)求 的值;
的值;
(2)由频率分布表直方图可以认为,此次问卷调查的得分 近似服从正态分布
近似服从正态分布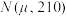 ,
, 近似为1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求 ;
;
(3)在(2)的条件下,文明办为此次参加问卷调查的市民制定如下的奖励方案:
①得分不低于 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于 的可以获赠1次随机话费;
的可以获赠1次随机话费;
②每次赠送的随机话费和对应的概率为:
记 (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求 的分布列和数学期望.
的分布列和数学期望.
附: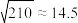 .若
.若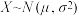 ,则①
,则①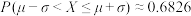 ②
②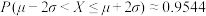 ③
③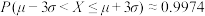

(1)求
 的值;
的值;(2)由频率分布表直方图可以认为,此次问卷调查的得分
 近似服从正态分布
近似服从正态分布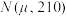 ,
, 近似为1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求 ;
;(3)在(2)的条件下,文明办为此次参加问卷调查的市民制定如下的奖励方案:
①得分不低于
 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于 的可以获赠1次随机话费;
的可以获赠1次随机话费;②每次赠送的随机话费和对应的概率为:
| 赠送的随机话费(单位:元) | 20 | 40 |
| 概率 |  |  |
 (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求 的分布列和数学期望.
的分布列和数学期望.附:
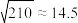 .若
.若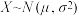 ,则①
,则①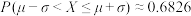 ②
②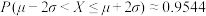 ③
③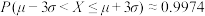
您最近一年使用:0次
名校
3 . 为抢占市场,特斯拉电动车近期进行了一系列优惠促销方案.要保证品质兼优,特斯拉上海工厂在车辆出厂前抽取100辆Model3型汽车作为样本进行了单次最大续航里程的测试.现对测试数据进行分析,得到如图所示的频率分布直方图:
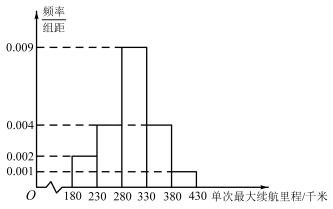
(1)估计这100辆汽车的单次最大续航里程的平均值(同一组中的数据用该组区间的中点值代替).
(2)根据大量的测试数据,可以认为Model3这款汽车的单次最大续航里程 近似地服从正态分布
近似地服从正态分布 ,经计算第(1)问中样本标准差s的近似值为50.用样本平均数
,经计算第(1)问中样本标准差s的近似值为50.用样本平均数 作为
作为 的近似值,用样本标准差s作为
的近似值,用样本标准差s作为 的估计值,现从生产线下任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率.
的估计值,现从生产线下任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率.
(3)为迅速抢占市场举行促销活动,特斯拉销售公司现面向意向客户推出“玩游戏,赢大奖,送车模”活动,客户可根据拋掷硬币的结果,指挥车模在方格图上行进,若车模最终停在“幸运之神”方格,则可获得购车优惠券6万元;若最终停在“赠送车模”方格时,则可获得车模一个.已知硬币出现正、反面的概率都是0.5,方格图上标有第0格、第1格、第2格、……、第20格.车模开始在第0格,客户每掷一次硬币,车模向前移动一次.若掷出正面,车模向前移动一格(从k到k+1),若掷出反面,车模向前移动两格(从k到k+2),直到移到第19格(幸运之神)或第20格(赠送车模)时游戏结束.设车模移到第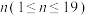 格的概率为
格的概率为 ,试证明
,试证明 是等比数列;若有6人玩游戏,每人参与一次,求这6人获得优惠券总金额的期望值(结果精确到1万元).
是等比数列;若有6人玩游戏,每人参与一次,求这6人获得优惠券总金额的期望值(结果精确到1万元).
参考数据:若随机变量 服从正态分布
服从正态分布 ,则
,则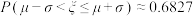
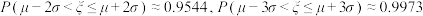

(1)估计这100辆汽车的单次最大续航里程的平均值(同一组中的数据用该组区间的中点值代替).
(2)根据大量的测试数据,可以认为Model3这款汽车的单次最大续航里程
 近似地服从正态分布
近似地服从正态分布 ,经计算第(1)问中样本标准差s的近似值为50.用样本平均数
,经计算第(1)问中样本标准差s的近似值为50.用样本平均数 作为
作为 的近似值,用样本标准差s作为
的近似值,用样本标准差s作为 的估计值,现从生产线下任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率.
的估计值,现从生产线下任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率.(3)为迅速抢占市场举行促销活动,特斯拉销售公司现面向意向客户推出“玩游戏,赢大奖,送车模”活动,客户可根据拋掷硬币的结果,指挥车模在方格图上行进,若车模最终停在“幸运之神”方格,则可获得购车优惠券6万元;若最终停在“赠送车模”方格时,则可获得车模一个.已知硬币出现正、反面的概率都是0.5,方格图上标有第0格、第1格、第2格、……、第20格.车模开始在第0格,客户每掷一次硬币,车模向前移动一次.若掷出正面,车模向前移动一格(从k到k+1),若掷出反面,车模向前移动两格(从k到k+2),直到移到第19格(幸运之神)或第20格(赠送车模)时游戏结束.设车模移到第
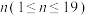 格的概率为
格的概率为 ,试证明
,试证明 是等比数列;若有6人玩游戏,每人参与一次,求这6人获得优惠券总金额的期望值(结果精确到1万元).
是等比数列;若有6人玩游戏,每人参与一次,求这6人获得优惠券总金额的期望值(结果精确到1万元).参考数据:若随机变量
 服从正态分布
服从正态分布 ,则
,则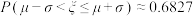
您最近一年使用:0次