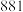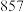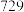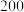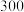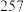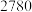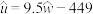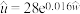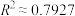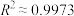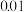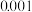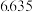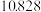解题方法
1 . 某地区5家超市销售额 (单位:万元)与广告支出
(单位:万元)与广告支出 (单位:万元)有如下一组数据:
(单位:万元)有如下一组数据:
下列说法正确的是( )
参考公式:样本相关系数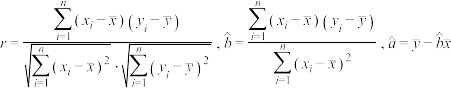
 (单位:万元)与广告支出
(单位:万元)与广告支出 (单位:万元)有如下一组数据:
(单位:万元)有如下一组数据:| 超市 | A | B | C | D | E |
| 广告支出(万元) | 1 | 4 | 6 | 10 | 14 |
| 销售额(万元) | 6 | 20 | 36 | 40 | 48 |
参考公式:样本相关系数
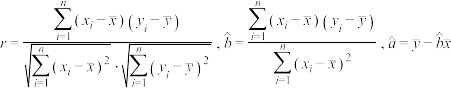
A.根据表中数据计算得到 与 与 之间的经验回归方程为 之间的经验回归方程为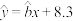 ,则 ,则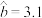 |
B. 与 与 之间的样本相关系数 之间的样本相关系数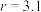 |
| C.若残差的平方和越小,则模型的拟合效果越好 |
| D.若该地区某超市的广告支出是3万元,则该超市的销售额一定是17.6万元 |
您最近一年使用:0次
名校
2 . 已知变量x,y之间的线性回归方程为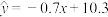 ,且变量x,y之间的一组相关数据如表所示,则下列说法正确的是( )
,且变量x,y之间的一组相关数据如表所示,则下列说法正确的是( )
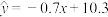 ,且变量x,y之间的一组相关数据如表所示,则下列说法正确的是( )
,且变量x,y之间的一组相关数据如表所示,则下列说法正确的是( )x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
| A.变量x,y之间呈现负相关关系 | B. |
C.可以预测,当 时,y约为2.6 时,y约为2.6 | D.由表格数据知,该回归直线必过点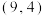 |
您最近一年使用:0次
解题方法
3 . 在每年的1月份到7月份,某品牌空调销售商发现:“每月销售量(单位:台)”与“当年的月份”线性相关.根据统计得下表:
(1)根据往年的统计得,当年的月份 与销量
与销量 满足回归方程
满足回归方程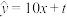 .请预测当年7月份该品牌的空调可以销售多少台?
.请预测当年7月份该品牌的空调可以销售多少台?
(2)该销售商从当年的前6个月中随机选取2个月,记 为销量不低于前6个月的月平均销量的月份数,求
为销量不低于前6个月的月平均销量的月份数,求 的分布列和数学期望
的分布列和数学期望
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销量 | 10 | 19 | 31 | 45 | 55 | 68 |
 与销量
与销量 满足回归方程
满足回归方程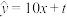 .请预测当年7月份该品牌的空调可以销售多少台?
.请预测当年7月份该品牌的空调可以销售多少台?(2)该销售商从当年的前6个月中随机选取2个月,记
 为销量不低于前6个月的月平均销量的月份数,求
为销量不低于前6个月的月平均销量的月份数,求 的分布列和数学期望
的分布列和数学期望
您最近一年使用:0次
解题方法
4 . 由于人们健康意识的提升,运动爱好者人群不断扩大,运动相关行业得到快速发展.某运动品牌专卖店从2019年至2023年的年销售额如下表:
(1)请根据表中的数据用最小二乘法求 与
与 的经验回归方程
的经验回归方程 ,并预测2024年该店的年销售额.
,并预测2024年该店的年销售额.
(2)该专卖店为了回馈广大消费者,推出了消费抽奖返现活动,规则如下:凡一次性消费满500元可抽奖1次,满1000元可抽奖2次.其中一次抽奖返现金额及概率如下表:
已知一位消费者一次性消费满500元的概率为 ,满1000元的概率为
,满1000元的概率为 ,求这位消费者抽奖返现金额
,求这位消费者抽奖返现金额 的分布列与期望.
的分布列与期望.
附:经验回归方程 中,
中,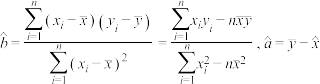 .
.
| 年份 | 2019 | 2020 | 2021 | 2022 | 2023 |
年份编号 | 1 | 2 | 3 | 4 | 5 |
年销售额 /万元 /万元 | 30 | 35 | 45 | 60 | 80 |
 与
与 的经验回归方程
的经验回归方程 ,并预测2024年该店的年销售额.
,并预测2024年该店的年销售额.(2)该专卖店为了回馈广大消费者,推出了消费抽奖返现活动,规则如下:凡一次性消费满500元可抽奖1次,满1000元可抽奖2次.其中一次抽奖返现金额及概率如下表:
| 返现金额 | 50 | 100 |
| 概率 |  |  |
 ,满1000元的概率为
,满1000元的概率为 ,求这位消费者抽奖返现金额
,求这位消费者抽奖返现金额 的分布列与期望.
的分布列与期望.附:经验回归方程
 中,
中,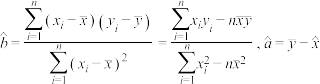 .
.
您最近一年使用:0次
解题方法
5 . 制定适合自己的学习计划并在学习过程中根据自己的实际情况有效地安排和调整学习方法是一种有效的学习策略.某教师为研究学生制定学习计划并坚持实施和数学成绩之间的关系,得到如下数据:
(1)依据小概率值 的独立性检验,能否认为“制定学习计划并坚持实施”和“数学成绩高于
的独立性检验,能否认为“制定学习计划并坚持实施”和“数学成绩高于 分”有关联?
分”有关联?
(2)若该校高三年级每月进行一次月考,该校学生小明在高三开学初认真制定了学习计划,其中一项要求自己每天要把错题至少重做一遍,做对为止.以下为小明坚持实施计划的月份和他在学校数学月考成绩的校内名次数据:
参考数据: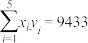 ,
,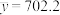 .
.
(ⅰ)求月考校内名次 与时间代码
与时间代码 的线性回归方程
的线性回归方程 ;
;
(ⅱ)该校老师给出了上一年该校学生高考( 月初考试)数学成绩在校内的名次和在全省名次的部分数据:
月初考试)数学成绩在校内的名次和在全省名次的部分数据:
利用数据分析软件,根据以上数据得出了两个回归模型和决定系数 :
:
在以上两个模型中选择“较好”模型(说明理由),并结合问题(ⅰ)的回归方程,依据“较好”模型预测小明如果能坚持实施学习计划,他在次年高考中数学成绩的全省名次(名次均保留整数).(参考数据: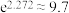 ,
, ,
,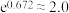 )
)
附:(ii) ,其中
,其中 .
.
(i)对于一组数据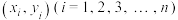 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: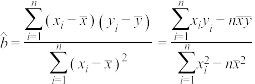 ,
, .
.
成绩 | 成绩 | 合计 | |
制定学习计划并坚持实施 |
|
|
|
没有制定学习计划 |
|
|
|
合计 |
|
|
|
(1)依据小概率值
 的独立性检验,能否认为“制定学习计划并坚持实施”和“数学成绩高于
的独立性检验,能否认为“制定学习计划并坚持实施”和“数学成绩高于 分”有关联?
分”有关联?(2)若该校高三年级每月进行一次月考,该校学生小明在高三开学初认真制定了学习计划,其中一项要求自己每天要把错题至少重做一遍,做对为止.以下为小明坚持实施计划的月份和他在学校数学月考成绩的校内名次数据:
月考时间 |
|
| 次年 | 次年 | 次年 |
时间代码 |
|
|
|
|
|
月考校内名次 |
|
|
|
|
|
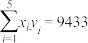 ,
,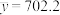 .
.(ⅰ)求月考校内名次
 与时间代码
与时间代码 的线性回归方程
的线性回归方程 ;
;(ⅱ)该校老师给出了上一年该校学生高考(
 月初考试)数学成绩在校内的名次和在全省名次的部分数据:
月初考试)数学成绩在校内的名次和在全省名次的部分数据:校内名次 |
|
|
|
|
全省名次 |
|
|
|
|
 :
:模型① | 模型② |
|
|
|
|
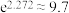 ,
, ,
,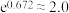 )
)附:(ii)
 ,其中
,其中 .
.
|
|
|
|
|
|
|
|
|
|
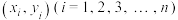 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: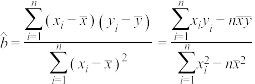 ,
, .
.
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
6 . 已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度 (单位
(单位 ),对某种鸡的时段产蛋量
),对某种鸡的时段产蛋量 (单位:
(单位:  )和时段投入成本
)和时段投入成本 (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度 和产蛋量
和产蛋量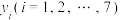 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
其中 ,
, 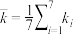 .
.
(1)根据散点图判断,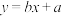 与
与 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量 关于鸡舍时段控制温度
关于鸡舍时段控制温度 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)
(2)若用 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立 关于
关于 的回归方程;
的回归方程;
(3)已知时段投入成本 与
与 的关系为
的关系为 ,当时段控制温度为
,当时段控制温度为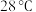 时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有线性相关关系的数据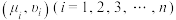 ,其回归直线
,其回归直线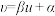 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为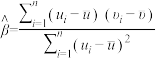 ,
, 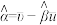
②
 (单位
(单位 ),对某种鸡的时段产蛋量
),对某种鸡的时段产蛋量 (单位:
(单位:  )和时段投入成本
)和时段投入成本 (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度 和产蛋量
和产蛋量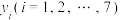 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.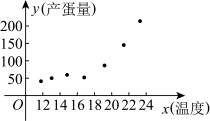
 | 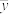 | 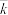 | 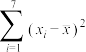 | 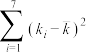 | 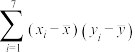 | 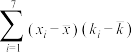 |
| 17.40 | 82.30 | 3.6 | 140 | 9.7 | 2935.1 | 35.0 |
 ,
, 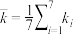 .
.(1)根据散点图判断,
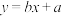 与
与 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量 关于鸡舍时段控制温度
关于鸡舍时段控制温度 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)(2)若用
 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立 关于
关于 的回归方程;
的回归方程;(3)已知时段投入成本
 与
与 的关系为
的关系为 ,当时段控制温度为
,当时段控制温度为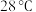 时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?附:①对于一组具有线性相关关系的数据
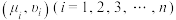 ,其回归直线
,其回归直线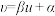 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为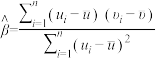 ,
, 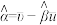
②
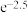 |  |  |  |  |
| 0.08 | 0.47 | 2.72 | 20.09 | 1096.63 |
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
7 . 预制菜指以农、畜、禽、水产品为原辅料,配以调味料等经预选、调制等工艺加工而成的半成品.近几年预制菜市场快速增长.某城市调查近4个月的预制菜市场规模y(万元)得到如表所示的数据,根据数据得到y关于x的非线性回归方程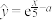
按照这样的速度,预估第8个月的预制菜市场规模是______ 万元.(结果用e表示)
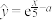
 | 1 | 2 | 3 | 4 |
 |  | 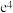 | 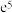 | 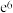 |
您最近一年使用:0次
解题方法
8 . 假设关于某设备的使用年限 和所支出的维修费用
和所支出的维修费用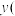 万元
万元 统计数据如下:
统计数据如下:
若有数据知 对
对 呈线性相关关系.其线形回归方程为
呈线性相关关系.其线形回归方程为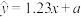 ,请估计使用
,请估计使用 年时的维修费用是
年时的维修费用是______ 万元.
 和所支出的维修费用
和所支出的维修费用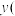 万元
万元 统计数据如下:
统计数据如下:使用年限 |  |  |  |  |  |
维修费用 |  |  |  | 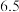 | 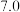 |
 对
对 呈线性相关关系.其线形回归方程为
呈线性相关关系.其线形回归方程为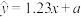 ,请估计使用
,请估计使用 年时的维修费用是
年时的维修费用是
您最近一年使用:0次
名校
解题方法
9 . 为践行“更快更高更强”的奥林匹克格言,落实全民健身国家战略.某校高三年级发起了“发扬奥林匹克精神,锻炼健康体魄”的年度主题活动,经过一段时间后,学生的身体素质明显提高.为了解活动效果,该年级对开展活动以来近6个月体重超重的人数进行了调查,调查结果统计如图,根据上面的散点图可以认为散点集中在曲线 的附近,请根据下表中的数据求出
的附近,请根据下表中的数据求出
(1)该年级体重超重人数y与月份x之间的经验回归方程 系数
系数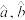 的最终结果精确到
的最终结果精确到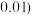 ;
;
(2)预测从开展活动以来第几个月份开始该年级体重超标的人数降至10人以下.
附:经验回归方程: 中,
中,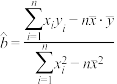 ,
, ;参考数据:
;参考数据: ,
,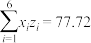 ,
,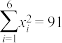 ,
,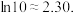
 的附近,请根据下表中的数据求出
的附近,请根据下表中的数据求出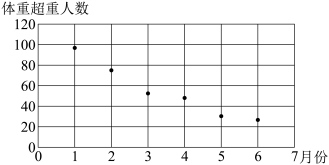
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 |
| 体重超标人数y | 98 | 77 | 54 | 48 | 32 | 27 |
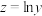 |  | 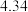 | 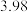 | 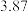 |  | 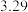 |
(1)该年级体重超重人数y与月份x之间的经验回归方程
 系数
系数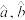 的最终结果精确到
的最终结果精确到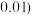 ;
;(2)预测从开展活动以来第几个月份开始该年级体重超标的人数降至10人以下.
附:经验回归方程:
 中,
中,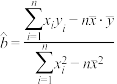 ,
, ;参考数据:
;参考数据: ,
,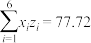 ,
,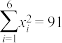 ,
,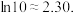
您最近一年使用:0次
10 . 每年3,4月间,成批白天鹅从地中海沿岸、南亚等温暖的地方越冬来到天山中部广袤的巴音布鲁克草原.为保护这些白天鹅,某动物保护机构研究了这时期6个区域每公顷草原的白天鹅平均只数y与每公顷草原上白天鹅的天敌狼和狐狸的平均只数x之间的对应数据,如下表所示:
根据表中的数据计算得经验回归方程为 ,则以下结论正确的是( )
,则以下结论正确的是( )
 | 10 | 15 | 20 | 25 | 30 |
 | 11 | 10 | 8 | 6 | 5 |
 ,则以下结论正确的是( )
,则以下结论正确的是( )A. 与 与 负相关 负相关 |
B.回归直线一定经过点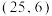 |
| C.估计当白天鹅的天敌每公顷平均只数为5时,白天鹅每公顷平均只数大约为13 |
D.当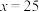 时,残差的绝对值最小 时,残差的绝对值最小 |
您最近一年使用:0次

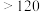 分
分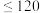 分
分




 月初
月初 月初
月初 月初
月初