解题方法
1 . 发展特色农业是我国农业结构战略调整的要求,某县为了响应国家的号召,特地承包了一块土地,已知土地的使用面积x(单位:公顷)与相应的管理时间y(单位:月)的关系如下表所示:
调查了某村300名村民参与管理的意愿,得到 列联表的部分数据如下表所示:
列联表的部分数据如下表所示:
(1)画出散点图,判断土地使用面积x与管理时间y是否线性相关,并根据相关系数r说明相关关系的强弱;(若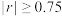 ,认为两个变量有很强的线性相关性,r值精确到0.001)
,认为两个变量有很强的线性相关性,r值精确到0.001)
(2)补全 列联表,并判断是否有99.9%的把握认为该村的村民的参与管理意愿与性别有关.
列联表,并判断是否有99.9%的把握认为该村的村民的参与管理意愿与性别有关.
参考公式:
参考数据: ,
,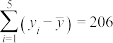 ,
,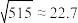 .
.
| 土地使用面积x | 1 | 2 | 3 | 4 | 5 |
| 管理时间y | 8 | 11 | 14 | 24 | 23 |
 列联表的部分数据如下表所示:
列联表的部分数据如下表所示:| 愿意参与管理 | 不愿意参与管理 | 总计 | |
| 男性村民 | 140 | 60 | |
| 女性村民 | 40 | ||
| 总计 |
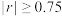 ,认为两个变量有很强的线性相关性,r值精确到0.001)
,认为两个变量有很强的线性相关性,r值精确到0.001)(2)补全
 列联表,并判断是否有99.9%的把握认为该村的村民的参与管理意愿与性别有关.
列联表,并判断是否有99.9%的把握认为该村的村民的参与管理意愿与性别有关.参考公式:

参考数据:
 ,
,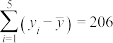 ,
,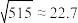 .
.
您最近一年使用:0次
2021-10-25更新
|
290次组卷
|
2卷引用:苏教版(2019) 选修第二册 名师精选 第九章 第九单元 独立性检验
名校
解题方法
2 . 求作一个立方体,使其体积等于已知立方体体积的2倍,这就是历史上有名的立方倍积问题.1837年法国数学家闻脱兹尔证明了立方倍积问题不能只用直尺与圆规作图来完成,不过人们发现,跳出直尺与圆规作图的框框,可以找到不同的作图方法.如图是柏拉图(公元前427—公元前347年)的方法:假设已知立方体的边长为 ,作两条互相垂直的直线,相交于点
,作两条互相垂直的直线,相交于点 ,在一条直线上截取
,在一条直线上截取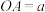 ,在另一条直线上截取
,在另一条直线上截取 ,在直线
,在直线 上分别取点
上分别取点 ,使
,使 (只要移动两个直角尺,使一个直角尺的边缘通过点
(只要移动两个直角尺,使一个直角尺的边缘通过点 ,另一个直角尺的边缘通过点
,另一个直角尺的边缘通过点 ,并使两直角尺的另一边重合,则两直角尺的直角顶点即为
,并使两直角尺的另一边重合,则两直角尺的直角顶点即为 ),则线段
),则线段 即为所求立方体的一边.以直线
即为所求立方体的一边.以直线 、
、 分别为
分别为 轴、
轴、 轴建立直角坐标系,若圆
轴建立直角坐标系,若圆 经过点
经过点 ,则圆
,则圆 的方程为
的方程为______ .
 ,作两条互相垂直的直线,相交于点
,作两条互相垂直的直线,相交于点 ,在一条直线上截取
,在一条直线上截取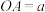 ,在另一条直线上截取
,在另一条直线上截取 ,在直线
,在直线 上分别取点
上分别取点 ,使
,使 (只要移动两个直角尺,使一个直角尺的边缘通过点
(只要移动两个直角尺,使一个直角尺的边缘通过点 ,另一个直角尺的边缘通过点
,另一个直角尺的边缘通过点 ,并使两直角尺的另一边重合,则两直角尺的直角顶点即为
,并使两直角尺的另一边重合,则两直角尺的直角顶点即为 ),则线段
),则线段 即为所求立方体的一边.以直线
即为所求立方体的一边.以直线 、
、 分别为
分别为 轴、
轴、 轴建立直角坐标系,若圆
轴建立直角坐标系,若圆 经过点
经过点 ,则圆
,则圆 的方程为
的方程为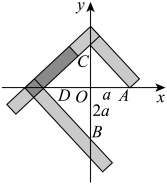
您最近一年使用:0次
名校
解题方法
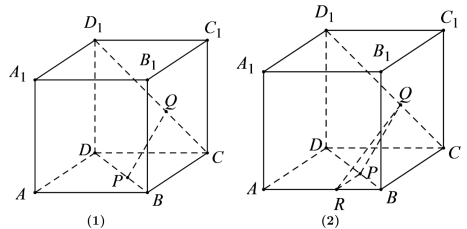
3 . 已知正方体 中,P、Q分别为对角线BD、
中,P、Q分别为对角线BD、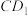 上的点,且
上的点,且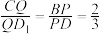 .
. 的交线(保留作图痕迹),并求证:
的交线(保留作图痕迹),并求证: 平面
平面 ;
;
(2)若R是AB上的点,当 的值为多少时,能使平面
的值为多少时,能使平面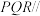 平面
平面 ?请给出证明.
?请给出证明.
 中,P、Q分别为对角线BD、
中,P、Q分别为对角线BD、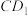 上的点,且
上的点,且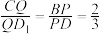 .
.
 的交线(保留作图痕迹),并求证:
的交线(保留作图痕迹),并求证: 平面
平面 ;
;(2)若R是AB上的点,当
 的值为多少时,能使平面
的值为多少时,能使平面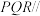 平面
平面 ?请给出证明.
?请给出证明.
您最近一年使用:0次
2021-11-19更新
|
1457次组卷
|
13卷引用:【课后练】10.4.1平面与平面平行 课后作业-沪教版(2020)必修第三册第10章 空间直线与平面
【课后练】10.4.1平面与平面平行 课后作业-沪教版(2020)必修第三册第10章 空间直线与平面上海市浦东新区南汇中学2021-2022学年高二上学期10月月考数学试题(已下线)第10课时 课后 空间中平面与平面的平行(已下线)8.5空间直线、平面的平行C卷(已下线)8.5 空间直线、平面的平行(已下线)第01讲 空间直线与平面(核心考点讲与练)(2)(已下线)高二数学上学期【第一次月考卷】(测试范围:第10~11章)-2022-2023学年高二数学考试满分全攻略(沪教版2020必修第一册)(已下线)10.4 平面与平面平行(第1课时)(作业)(夯实基础+能力提升)-【教材配套课件+作业】2022-2023学年高二数学精品教学课件(沪教版2020必修第三册)(已下线)8.5空间直线、平面的平行——课后作业(提升版)(已下线)压轴专题01 线面平行,垂直证明中补全条件问题-【常考压轴题】(沪教版2020必修第三册)(已下线)第08练 点线面的位置关系-2022年【暑假分层作业】高一数学(苏教版2019必修第二册)(已下线)第30讲 平面与平面平行(已下线)8.5.3 平面与平面平行 (精讲)(1)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)
名校
解题方法
4 . 在正方体 中,
中, 是棱
是棱 的中点.
的中点. 与平面
与平面 的交线,保留作图痕迹;
的交线,保留作图痕迹;
(2)在棱 上是否存在一点
上是否存在一点 ,使得
,使得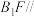 平面
平面 ,若存在,说明点
,若存在,说明点 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
 中,
中, 是棱
是棱 的中点.
的中点.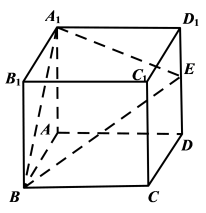
 与平面
与平面 的交线,保留作图痕迹;
的交线,保留作图痕迹;(2)在棱
 上是否存在一点
上是否存在一点 ,使得
,使得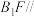 平面
平面 ,若存在,说明点
,若存在,说明点 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
您最近一年使用:0次
2021-10-08更新
|
722次组卷
|
9卷引用:2023版 北师大版(2019) 选修第一册 突围者 第三章 第五节 数学探究活动(一):正方体截面探究
2023版 北师大版(2019) 选修第一册 突围者 第三章 第五节 数学探究活动(一):正方体截面探究2023版 北师大版(2019) 选修第一册 突围者 第三章 第五节 数学探究活动(一):正方体截面探究上海市第二中学2017-2018学年高二下学期期中数学试题上海市徐汇中学2021-2022学年高二上学期9月月考数学试题(已下线)第04讲线线、线面、面面平行的判定与性质(核心考点讲与练)(1)上海海事大学附属北蔡高级中学2022-2023学年高二上学期12月月考数学试题(已下线)第10章 空间直线与平面(单元基础卷)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)8.5空间直线、平面的平行——课后作业(基础版)(已下线)压轴专题01 线面平行,垂直证明中补全条件问题-【常考压轴题】(沪教版2020必修第三册)
名校
5 . 如图,在长方体 中,
中,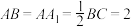 ,
, ,
, 分别为
分别为 与
与 中点.
中点. ,
, 作平面
作平面 ,平面
,平面 与长方体
与长方体 六个表面所截的截面可能是
六个表面所截的截面可能是 边形,请根据
边形,请根据 的不同的取值分别作出截面图形形状(每种情况找一个代表类型,例如
的不同的取值分别作出截面图形形状(每种情况找一个代表类型,例如 只需要画一种,下面给了四幅图,可以不用完,如果不够请自行增加),保留作图痕迹;
只需要画一种,下面给了四幅图,可以不用完,如果不够请自行增加),保留作图痕迹;
(2)若 为直线
为直线 上的一点,且
上的一点,且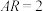 ,求过
,求过 截面图形的周长.
截面图形的周长.
 中,
中,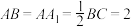 ,
, ,
, 分别为
分别为 与
与 中点.
中点.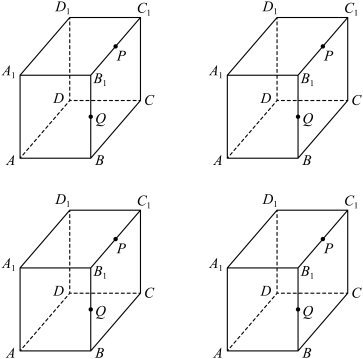
 ,
, 作平面
作平面 ,平面
,平面 与长方体
与长方体 六个表面所截的截面可能是
六个表面所截的截面可能是 边形,请根据
边形,请根据 的不同的取值分别作出截面图形形状(每种情况找一个代表类型,例如
的不同的取值分别作出截面图形形状(每种情况找一个代表类型,例如 只需要画一种,下面给了四幅图,可以不用完,如果不够请自行增加),保留作图痕迹;
只需要画一种,下面给了四幅图,可以不用完,如果不够请自行增加),保留作图痕迹;(2)若
 为直线
为直线 上的一点,且
上的一点,且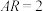 ,求过
,求过 截面图形的周长.
截面图形的周长.
您最近一年使用:0次
2020-05-07更新
|
295次组卷
|
5卷引用:【课后练】11.3 多面体与旋转体 课后作业-沪教版(2020)必修第三册第11章 简单几何体
2020高三·全国·专题练习
真题
解题方法
6 . (1)求右焦点坐标是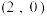 ,且经过点
,且经过点 的椭圆的标准方程;
的椭圆的标准方程;
(2)已知椭圆 的方程是
的方程是
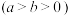 .设斜率为
.设斜率为 的直线
的直线 ,交椭圆
,交椭圆 于
于
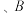 两点,
两点, 的中点为
的中点为 .证明:当直线
.证明:当直线 平行移动时,动点
平行移动时,动点 在一条过原点的定直线上;
在一条过原点的定直线上;
(3)利用(2)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.
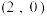 ,且经过点
,且经过点 的椭圆的标准方程;
的椭圆的标准方程;(2)已知椭圆
 的方程是
的方程是
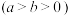 .设斜率为
.设斜率为 的直线
的直线 ,交椭圆
,交椭圆 于
于
 两点,
两点, 的中点为
的中点为 .证明:当直线
.证明:当直线 平行移动时,动点
平行移动时,动点 在一条过原点的定直线上;
在一条过原点的定直线上;(3)利用(2)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.
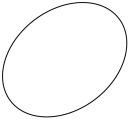
您最近一年使用:0次
2020-05-26更新
|
547次组卷
|
4卷引用:沪教版(2020) 选修第一册 领航者 第2章 2.2椭圆 第2课时 椭圆的性质(1)
沪教版(2020) 选修第一册 领航者 第2章 2.2椭圆 第2课时 椭圆的性质(1)【课堂例】2.2.2 椭圆的性质(1) 课堂例题 沪教版(2020)选择性必修第一册 第2章 圆锥曲线(已下线)秒杀题型09 圆锥曲线中的中点弦-2020年高考数学试题调研之秒杀圆锥曲线压轴题2005年普通高等学校春季招生考试数学试题(上海卷)
解题方法
7 . 如图,在四棱锥 的底面ABCD中,
的底面ABCD中,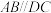 .回答下面的问题:
.回答下面的问题: 内能否作一条线段,使其与DC平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由;
内能否作一条线段,使其与DC平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由;
(2)在侧面PBC中能否作出一条线段,使其与AD平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由.
 的底面ABCD中,
的底面ABCD中,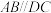 .回答下面的问题:
.回答下面的问题: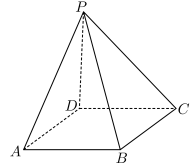
 内能否作一条线段,使其与DC平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由;
内能否作一条线段,使其与DC平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由;(2)在侧面PBC中能否作出一条线段,使其与AD平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由.
您最近一年使用:0次
2021-11-12更新
|
309次组卷
|
6卷引用:第十一章 立体几何初步 11.3 空间中的平行关系 11.3.3 平面与平面平行
(已下线)第十一章 立体几何初步 11.3 空间中的平行关系 11.3.3 平面与平面平行人教B版(2019) 必修第四册 逆袭之路 第十一章 立体几何初步 11.3空间中的平行关系(已下线)第十三章本章测试(已下线)8.5 空间直线、平面的平行人教B版(2019)必修第四册课本习题习题11-3苏教版(2019)必修第二册课本习题第13章本章测试
解题方法
8 . 某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成 ,
,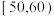 ,
,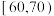 ,
,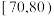 ,
,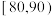 ,
,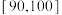 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题: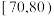 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的众数和中位数和平均数.
 ,
,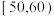 ,
,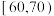 ,
,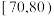 ,
,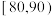 ,
,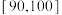 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题: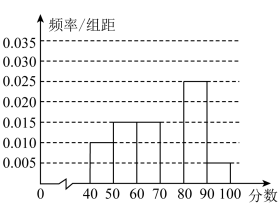
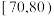 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;(2)从频率分布直方图中,估计本次考试成绩的众数和中位数和平均数.
您最近一年使用:0次
2022-10-25更新
|
1276次组卷
|
8卷引用:13.4统计图表(作业)(夯实基础+能力提升)-【教材配套课件+作业】2022-2023学年高二数学精品教学课件(沪教版2020必修第三册)
13.4统计图表(作业)(夯实基础+能力提升)-【教材配套课件+作业】2022-2023学年高二数学精品教学课件(沪教版2020必修第三册)(已下线)第13章 统计(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(沪教版2020必修第三册)黑龙江省肇东市第四中学2021-2022学年高一下学期期末考试数学试题(已下线)第六章 统计(A卷·知识通关练)-【单元测试】2022-2023学年高一数学分层训练AB卷(北师大版2019必修第一册)(已下线)第39讲 频率分布直方图、总体取值规律、总体百分位数的估计5种常考题型)江西省宜春市丰城第九中学日新部2022-2023学年高一上学期期末数学试题(已下线)复习专题10用样本数据估计总体(1)-期末专项复习山东省聊城颐中外国语学校2023-2024学年高一下学期第三次质量检测数学试题
解题方法
9 . 北京2022年冬奥会于2022年2月4日至2022年2月20日在中国北京市和中国河北省张家口市联合举行.这是中国历史上第一次举办冬季奥运会,北京、张家口同为主办城市,也是中国继北京奥运会、南京青奥会之后第三次举办奥运赛事.北京冬奥组委对报名参加北京冬奥会志愿者的人员开展冬奥会志愿者的培训活动,并在培训结束后进行了一次考核.为了解本次培训活动的效果,从中随机抽取80名志愿者的考核成绩,根据这80名志愿者的考核成绩,得到的统计图表如下所示.
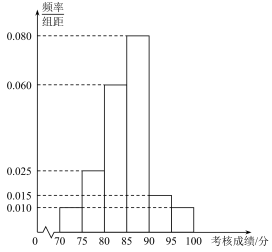
男志愿者考核成绩频率分布直方图
女志愿者考核成绩频率分布表
若参加这次考核的志愿者考核成绩在[90,100]内,则考核等级为优秀.
(1)分别求这次培训考核等级为优秀的男、女志愿者人数;
(2)补全下面的2×2列联表,并判断是否有95%的把握认为考核等级是否是优秀与性别有关.

男志愿者考核成绩频率分布直方图
女志愿者考核成绩频率分布表
分组 | 频数 | 频率 |
[75,80) | 2 | 0.05 |
[80,85) | 13 | 0.325 |
[85,90) | 12 | 0.3 |
[90,95) | a | m |
[95,100] | b | 0.075 |
(1)分别求这次培训考核等级为优秀的男、女志愿者人数;
(2)补全下面的2×2列联表,并判断是否有95%的把握认为考核等级是否是优秀与性别有关.
性别 考核等级 | 优秀 | 非优秀 | 总计 |
男 | |||
女 | |||
总计 |
您最近一年使用:0次
10 . 有甲、乙两个班级进行数学考试,若规定成绩在85分及以上为优秀,85分以下为非优秀,统计成绩后,得到如下的列联表.
已知从105个学生中随机抽取1人,其数学成绩为优秀的概率为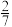 .
.
(1)请根据已知条件补全上面的列联表;
(2)依据 的独立性检验,能否认为学生的数学成绩与班级有关?
的独立性检验,能否认为学生的数学成绩与班级有关?
(3)若按下面的方法从甲班数学成绩为优秀的学生中抽取1人:把甲班数学成绩为优秀的10名学生按2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的编号(注:出现的点数之和为12时,被抽取人的编号为2),试求抽到4号或9号的概率.
单位:人 | |||
班级 | 数学成绩 | 合计 | |
优秀 | 非优秀 | ||
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 105 | ||
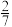 .
.(1)请根据已知条件补全上面的列联表;
(2)依据
 的独立性检验,能否认为学生的数学成绩与班级有关?
的独立性检验,能否认为学生的数学成绩与班级有关?(3)若按下面的方法从甲班数学成绩为优秀的学生中抽取1人:把甲班数学成绩为优秀的10名学生按2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的编号(注:出现的点数之和为12时,被抽取人的编号为2),试求抽到4号或9号的概率.
您最近一年使用:0次



