1 . 设 是定义在
是定义在 上的函数,满足
上的函数,满足 ,且对任意
,且对任意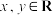 ,
,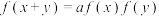 (
( 为常数),点
为常数),点 在曲线
在曲线 上,
上, 为数列
为数列 的前
的前 项和,则下列说法正确的有( ).
项和,则下列说法正确的有( ).
 是定义在
是定义在 上的函数,满足
上的函数,满足 ,且对任意
,且对任意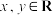 ,
,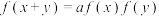 (
( 为常数),点
为常数),点 在曲线
在曲线 上,
上, 为数列
为数列 的前
的前 项和,则下列说法正确的有( ).
项和,则下列说法正确的有( ).A. 的解析式可能为 的解析式可能为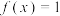 |
B.若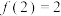 ,则 ,则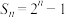 |
C.若 在 在 上是增函数,则 上是增函数,则 |
D.若 ,则 ,则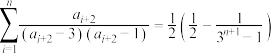 |
您最近一年使用:0次
2 . 若数列 和
和 的项数均为
的项数均为 ,则将数列
,则将数列 和
和 的距离定义为
的距离定义为 .
.
(1)求数列1,3,5,6和数列2,3,10,7的距离;
(2)记A为满足递推关系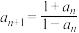 的所有数列
的所有数列 的集合,数列
的集合,数列 和
和 为A中的两个元素,且项数均为
为A中的两个元素,且项数均为 .若
.若 ,
, ,数列
,数列 和
和 的距离
的距离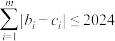 ,求m的最大值;
,求m的最大值;
(3)记S是所有7项数列 (其中
(其中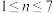 ,
, 或1)的集合,
或1)的集合,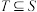 ,且T中的任何两个元素的距离大于或等于3.求证:T中的元素个数小于或等于16.
,且T中的任何两个元素的距离大于或等于3.求证:T中的元素个数小于或等于16.
 和
和 的项数均为
的项数均为 ,则将数列
,则将数列 和
和 的距离定义为
的距离定义为 .
.(1)求数列1,3,5,6和数列2,3,10,7的距离;
(2)记A为满足递推关系
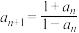 的所有数列
的所有数列 的集合,数列
的集合,数列 和
和 为A中的两个元素,且项数均为
为A中的两个元素,且项数均为 .若
.若 ,
, ,数列
,数列 和
和 的距离
的距离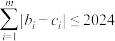 ,求m的最大值;
,求m的最大值;(3)记S是所有7项数列
 (其中
(其中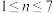 ,
, 或1)的集合,
或1)的集合,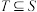 ,且T中的任何两个元素的距离大于或等于3.求证:T中的元素个数小于或等于16.
,且T中的任何两个元素的距离大于或等于3.求证:T中的元素个数小于或等于16.
您最近一年使用:0次
2024-05-20更新
|
382次组卷
|
3卷引用:贵州省六盘水市2023-2024学年高二下学期5月期中质量监测数学试题
3 . 已知椭圆 的焦点坐标
的焦点坐标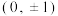 ,且过点
,且过点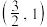 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)直线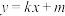 与椭圆
与椭圆 交于
交于 ,
, 两点,且
两点,且 ,
, 关于原点的对称点分别为
关于原点的对称点分别为 ,
, ,若
,若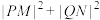 是一个与
是一个与 无关的常数,求此时的常数及四边形
无关的常数,求此时的常数及四边形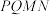 面积的最大值.
面积的最大值.
 的焦点坐标
的焦点坐标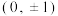 ,且过点
,且过点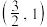 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)直线
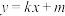 与椭圆
与椭圆 交于
交于 ,
, 两点,且
两点,且 ,
, 关于原点的对称点分别为
关于原点的对称点分别为 ,
, ,若
,若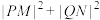 是一个与
是一个与 无关的常数,求此时的常数及四边形
无关的常数,求此时的常数及四边形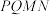 面积的最大值.
面积的最大值.
您最近一年使用:0次
2024-01-24更新
|
315次组卷
|
3卷引用:贵州省铜仁市2023-2024学年高二上学期1月期末质量监测数学试题
贵州省铜仁市2023-2024学年高二上学期1月期末质量监测数学试题江西省上高二中2024届高三适应性考试数学试卷(已下线)湖北省武汉市(武汉六中)部分重点中学2024届高三第二次联考数学试题变式题17-22
名校
解题方法
4 . 在平面直角坐标系xOy中,已知点 ,
,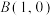 ,设
,设 的内切圆与AC相切于点D,且
的内切圆与AC相切于点D,且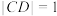 ,记动点C的轨迹为曲线T.
,记动点C的轨迹为曲线T.
(1)求T的方程;
(2)设过点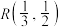 的直线l与T交于M,N两点,已知动点P满足
的直线l与T交于M,N两点,已知动点P满足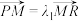 ,且
,且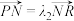 ,若
,若 ,且动点Q在T上,求
,且动点Q在T上,求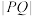 的最小值.
的最小值.
 ,
,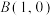 ,设
,设 的内切圆与AC相切于点D,且
的内切圆与AC相切于点D,且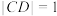 ,记动点C的轨迹为曲线T.
,记动点C的轨迹为曲线T.(1)求T的方程;
(2)设过点
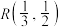 的直线l与T交于M,N两点,已知动点P满足
的直线l与T交于M,N两点,已知动点P满足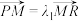 ,且
,且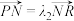 ,若
,若 ,且动点Q在T上,求
,且动点Q在T上,求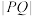 的最小值.
的最小值.
您最近一年使用:0次
2022-05-27更新
|
3182次组卷
|
5卷引用:贵州省贵阳市“三新”改革联盟校2022-2023学年高二上学期月考(六)数学试题
贵州省贵阳市“三新”改革联盟校2022-2023学年高二上学期月考(六)数学试题湖北省武汉市新洲区第一中学2022-2023学年高二下学期开学收心考试数学试题名校联盟山东省优质校2022届高三毕业班5月模拟考试数学试题(已下线)专题6 圆锥曲线硬解定理 微点2 圆锥曲线硬解定理综合训练(已下线)重难点15七种圆锥曲线的应用解题方法-3
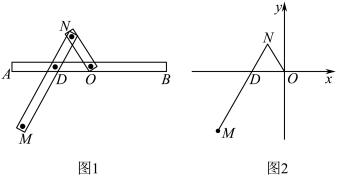
5 . 一种作图工具如图1所示. 是滑槽
是滑槽 的中点,短杆
的中点,短杆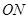 可绕
可绕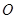 转动,长杆
转动,长杆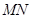 通过
通过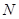 处铰链与
处铰链与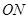 连接,
连接,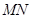 上的栓子
上的栓子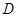 可沿滑槽AB滑动,且
可沿滑槽AB滑动,且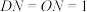 ,
,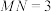 .当栓子
.当栓子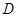 在滑槽AB内做往复运动时,带动
在滑槽AB内做往复运动时,带动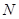 绕
绕 转动一周(
转动一周(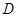 不动时,
不动时,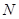 也不动),
也不动),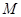 处的笔尖画出的曲线记为
处的笔尖画出的曲线记为 .以
.以 为原点,
为原点, 所在的直线为
所在的直线为 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
(Ⅰ)求曲线C的方程;
(Ⅱ)设动直线 与两定直线
与两定直线 和
和 分别交于
分别交于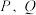 两点.若直线
两点.若直线 总与曲线
总与曲线 有且只有一个公共点,试探究:
有且只有一个公共点,试探究: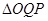 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
 是滑槽
是滑槽 的中点,短杆
的中点,短杆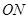 可绕
可绕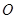 转动,长杆
转动,长杆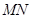 通过
通过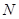 处铰链与
处铰链与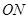 连接,
连接,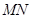 上的栓子
上的栓子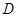 可沿滑槽AB滑动,且
可沿滑槽AB滑动,且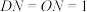 ,
,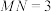 .当栓子
.当栓子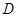 在滑槽AB内做往复运动时,带动
在滑槽AB内做往复运动时,带动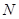 绕
绕 转动一周(
转动一周(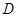 不动时,
不动时,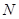 也不动),
也不动),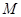 处的笔尖画出的曲线记为
处的笔尖画出的曲线记为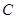 .以
.以 为原点,
为原点, 所在的直线为
所在的直线为 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
(Ⅰ)求曲线C的方程;
(Ⅱ)设动直线
 与两定直线
与两定直线 和
和 分别交于
分别交于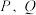 两点.若直线
两点.若直线 总与曲线
总与曲线 有且只有一个公共点,试探究:
有且只有一个公共点,试探究: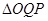 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
您最近一年使用:0次
2016-12-03更新
|
4986次组卷
|
15卷引用:贵州省遵义市南白中学2022-2023学年高二下学期第一次联考数学试题
贵州省遵义市南白中学2022-2023学年高二下学期第一次联考数学试题北京市北京一零一中学2019-2020学年高二第一学期期末考试数学试题北京市101中学2019-2020学年上学期高二年级期末考试数学试题安徽省马鞍山市第二中学2020-2021学年高二上学期期末理科数学试题2015年全国普通高等学校招生统一考试理科数学(湖北卷)2015年全国普通高等学校招生统一考试文科数学(湖北卷)(已下线)上海市华东师范大学第二附属中学2017-2018学年高三上学期10月月考数学试题(已下线)专题29 圆锥曲线的综合问题-十年(2011-2020)高考真题数学分项(已下线)专题22 圆锥曲线的“三定”与探索性问题(讲)-2021年高三数学二轮复习讲练测(新高考版)(已下线) 专题26 圆锥曲线的“三定”与探索性问题(讲)-2021年高三数学二轮复习讲练测(文理通用)(已下线)专题23 圆锥曲线中的最值、范围问题 微点1 圆锥曲线中的最值问题(已下线)专题24 解析几何解答题(文科)-4(已下线)专题24 解析几何解答题(理科)-3专题36平面解析几何解答题(第一部分)专题37平面解析几何解答题(第一部分)



