18-19高一下·湖北襄阳·期中
名校
1 . 中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G,然而这并没有让华为却步.华为在2019年不仅净利润创下记录,海外增长同样强劲.今年,我国某一企业为了进一步增加市场竞争力,计划在2021年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产 (千部)手机,需另投入成本
(千部)手机,需另投入成本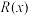 万元,且
万元,且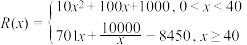 ,由市场调研知,每
,由市场调研知,每部 手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(1)求2021年的利润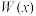 (万元)关于年产量
(万元)关于年产量 (千部)的函数关系式,(利润=销售额—成本);
(千部)的函数关系式,(利润=销售额—成本);
(2)2021年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
 (千部)手机,需另投入成本
(千部)手机,需另投入成本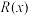 万元,且
万元,且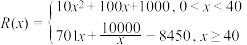 ,由市场调研知,每
,由市场调研知,每(1)求2021年的利润
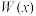 (万元)关于年产量
(万元)关于年产量 (千部)的函数关系式,(利润=销售额—成本);
(千部)的函数关系式,(利润=销售额—成本);(2)2021年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
您最近一年使用:0次
2020-11-12更新
|
2077次组卷
|
38卷引用:【新东方】杭州新东方高中数学试卷314
(已下线)【新东方】杭州新东方高中数学试卷314(已下线)第二章 (综合培优)一元二次函数、方程和不等式 B卷-【双基双测】2021-2022学年高一数学同步AB卷(浙江专用)(人教A版2019必修第一册)【校级联考】湖北省四校(襄州一中、枣阳一中、宜城一中、曾都一中)2018-2019学年高一下学期期中联考数学试题河南省鹤壁市高级中学2019-2020学年高一上学期第二次段考数学试题江西省赣州市南康中学2019-2020学年高一上学期12月月考数学试题河南省平顶山市鲁山一中2019-2020学年高一上学期12月月考数学试题四川省仁寿县第二中学、华兴中学2019-2020学年高一上学期期末模拟数学试题安徽省安庆市第二中学2019-2020学年高一上学期期中数学试题福建省漳州市龙海市程溪中学2019-2020学年高一上学期期中数学试题湖南省长沙市浏阳市2019-2020学年高二上学期期末数学试题(已下线)[新教材精创] 2.2基本不等式练习(1) -人教A版高中数学必修第一 册宁夏银川二中2019-2020学年高一年级下学期期末考试数学试题湖北省武汉市第三中学2019-2020学年高一下学期5月月考数学试题福建省龙岩市武平县第一中学2020-2021学年高一单元检测数学试题湖北省黄石市2020-2021学年高一上学期10月调研考试数学试题江苏省淮安市六校联盟2020-2021学年高一上学期第二次学情调查数学试题江苏省扬州市高邮市2020-2021学年高一上学期期中学情调研数学试题广东省深圳市盐田高级中学2020~2021学年高一上学期期中数学试题江苏省南京市2020-2021学年高一上学期第二次学情检测数学试题安徽省安庆市第九中学2020-2021学年高一上学期期中数学试题湖北省黄冈市黄州区第一中学2020-2021学年高一上学期期中数学试题广东省深圳市皇御苑学校2020-2021学年高一上学期期中数学试题重庆市渝东六校共同体2020-2021学年高一上学期联合诊断性测试数学试题(已下线)8.3+应用与建模++体重与脉搏(重点练)-2020-2021学年高一数学十分钟同步课堂专练(苏教版2019必修第一册)湖北省黄冈市外国语学校2020-2021学年高一上学期12月月考数学试题河北省安平中学2020-2021学年高一上学期第三次月考数学试题江西省石城中学2020-2021学年高一上学期第二次月考数学试题安徽省淮南五中2020-2021学年高三上学期第一次月考理科数学试题江苏省泰州市靖江市斜桥中学与刘国钧中学2020-2021学年高一上学期联考数学试题(已下线)必修第一册 (综合培优)数学全册检测题 B卷-【双基双测】2021-2022学年高一数学同步单元AB卷(人教A版2019必修第一册,广东专用)(已下线)江苏省南通市如皋市2020-2021学年高一下学期期初开学模拟考试数学试题(已下线)2.2 (分层练)基本不等式-2021-2022学年高中数学必修第一册课时解读与训练(人教A版2019)四川省内江市内江市第六中学2021-2022学年高一上学期第二次月考数学试题安徽师范大学附属中学2022-2023学年高一上学期期末模拟数学试题吉林省田家炳高级中学2022-2023学年高一上学期期末数学试题上海市奉贤区曙光中学2022届高三上学期10月月考数学试题重庆市石柱回龙中学校2024届高三上学期第一次月考数学试题新疆维吾尔自治区乌鲁木齐市第六十一中学2024届高考复习必修一练习卷
19-20高二·全国·课后作业
2 . 某批发商以每吨20元的价格购进一批建筑材料,若以每吨M元零售,销量N(单位:吨)与零售价M(单位:元)有如下关系: ,则该批材料零售价定为
,则该批材料零售价定为_______ 元时利润最大,利润的最大值为_________ 元.
 ,则该批材料零售价定为
,则该批材料零售价定为
您最近一年使用:0次
2020-12-03更新
|
436次组卷
|
4卷引用:专题5.4 《一元函数的导数及其应用》单元测试卷(B卷提升篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教A版,浙江专用)
(已下线)专题5.4 《一元函数的导数及其应用》单元测试卷(B卷提升篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教A版,浙江专用)人教A版(2019) 选择性必修第二册 过关斩将 第五章 一元函数的导数及其应用 5.3 导数在研究函数中的应用 5.3.2 函数的极值与最大(小)值 第2课时 函数的最大(小)值(已下线)专题12 导数在函数有关问题及实际生活中的应用 核心素养练习 -【新教材精创】2020-2021学年高二数学新教材知识讲学(人教A版选择性必修第二册)广东省佛山市实验中学2020-2021学年高二下学期阶段考试(一)数学试题
18-19高一下·江苏南京·期中
名校
3 . 为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用新工艺,把二氧化碳转化为一种可利用的产品.已知该单位每月处理二氧化碳最少400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似表示为y= x2-200x+80000,且每处理1吨二氧化碳得到可利用的化工产品价值为100元.
x2-200x+80000,且每处理1吨二氧化碳得到可利用的化工产品价值为100元.
(1)若该单位每月成本(每月成本=每月处理成本-每月可利用的化工产品价值)支出不超过105000元,求月处理量x的取值范围.
(2)该单位每月能否获利?如果能获利,求出能获得的最大利润;如果不能获利,那么国家每月至少补贴多少元,才能使该单位不亏损?
 x2-200x+80000,且每处理1吨二氧化碳得到可利用的化工产品价值为100元.
x2-200x+80000,且每处理1吨二氧化碳得到可利用的化工产品价值为100元.(1)若该单位每月成本(每月成本=每月处理成本-每月可利用的化工产品价值)支出不超过105000元,求月处理量x的取值范围.
(2)该单位每月能否获利?如果能获利,求出能获得的最大利润;如果不能获利,那么国家每月至少补贴多少元,才能使该单位不亏损?
您最近一年使用:0次
2020-07-18更新
|
368次组卷
|
6卷引用:专题2.2二次函数与一元二次方程、不等式(B卷提升篇)-2020-2021学年高一数学必修一同步单元AB卷(人教A版浙江专用)
(已下线)专题2.2二次函数与一元二次方程、不等式(B卷提升篇)-2020-2021学年高一数学必修一同步单元AB卷(人教A版浙江专用)江苏省南京市金陵中学2018-2019学年高一下学期期中数学试题(已下线)专题2.3 二次函数与一元二次方程、不等式(精练)-2021年新高考数学一轮复习学与练(已下线)第07讲 二次函数与一元二次方程、不等式(9大考点)-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)(已下线)专题08二次函数与一元一次方程、不等式-【倍速学习法】(人教A版2019必修第一册)(已下线)第二章+一元二次函数、方程和不等式(知识清单)-【满分全攻略】(人教A版2019必修第一册)
名校
解题方法
4 . 某汽车运输公司购买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润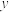 (单位:10万元)与营运年数
(单位:10万元)与营运年数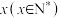 为二次函数关系(如图所示),则每辆客车营运( )年时,其营运的年平均利润
为二次函数关系(如图所示),则每辆客车营运( )年时,其营运的年平均利润 最大.
最大.

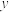 (单位:10万元)与营运年数
(单位:10万元)与营运年数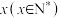 为二次函数关系(如图所示),则每辆客车营运( )年时,其营运的年平均利润
为二次函数关系(如图所示),则每辆客车营运( )年时,其营运的年平均利润 最大.
最大.
| A.3 | B.4 | C.5 | D.6 |
您最近一年使用:0次
2022-10-26更新
|
1685次组卷
|
32卷引用:人教A版(2019) 必修第一册(上) 重难点知识清单 第二章 一元二次函数、方程和不等式 单元学能测评
人教A版(2019) 必修第一册(上) 重难点知识清单 第二章 一元二次函数、方程和不等式 单元学能测评(已下线)第03章不等式(A卷基础篇)-2020-2021学年高二数学必修五同步单元AB卷(人教A版,浙江专用)(已下线)2012届大纲版高三上学期单元测试(6)数学试卷四川省眉山市2016-2017学年高一下学期期末考试数学试题广西桂林中学2017-2018学年高二上学期第一次月考(开学考试)数学试题(已下线)2019高考备考一轮复习精品资料 【理】专题十二 函数模型及其应用 押题专练(已下线)2019高考备考一轮复习精品资料 【文】专题十二 函数模型及其应用 押题专练(已下线)第3章 3.4 不等式的实际应用(分层训练)-2018-2019版数学创新设计课堂讲义同步系列(人教B版必修5)北京市第十五中学2019-2020学年第一学期期中高二数学试题(已下线)2.2+基本不等式-2020-2021高中数学新教材配套提升训练(人教A版必修第一册)第3章 不等式 单元综合测试卷-2022-2023学年高一数学新教材同步配套教学讲义(苏教版2019必修第一册)第8章 函数应用 单元综合测试卷-2022-2023学年高一数学新教材同步配套教学讲义(苏教版2019必修第一册)第五章 函数的应用 单元测试-2022-2023学年高一上学期数学北师大版(2019)必修第一册人教A版(2019) 必修第一册 章末检测卷(二) 一元二次函数、方程和不等式河北省保定市第三中学2020-2021学年高二下学期期末数学试题(已下线)第二单元 (基础过关)一元二次函数与方程、不等式 A卷-【双基双测】2021-2022学年高一数学同步单元AB卷(人教A版2019必修第一册)(已下线)第二单元 (综合培优)一元二次函数与方程、不等式 B卷-【双基双测】2021-2022学年高一数学同步单元AB卷(人教A版2019必修第一册)广东省揭阳市普宁市华侨中学2021-2022学年高一上学期第一次月考数学试题重庆市凤鸣山中学2021-2022学年高一上学期半期考试数学试题江苏省盐城市阜宁县2021-2022学年高一上学期期中数学试题(已下线)数学必修第一册期末测试-【上好课】2021-2022学年高一数学同步备课系列(人教A版2019必修第一册)江苏省盐城市五校2021-2022学年高一上学期期中联考数学试题(已下线)专题05 基本不等式的实际应用-2021-2022学年高一《新题速递·数学》(人教A版2019)苏教版(2019) 必修第一册 突围者 第3章 第二节 课时2 基本不等式的应用聚焦核心素养-一元二次函数、方程和不等式江苏省南京师范大学附属中学2022-2023学年高一上学期10月月考数学试题四川省眉山市彭山区第一中学2022-2023学年高一上学期10月月考数学试题山西省太原市第二外国语学校2022-2023学年高一上学期10月月考数学试卷重庆市凤鸣山中学教育集团2022-2023学年高一上学期期中数学试题广东省汕头市潮阳区棉城中学2022-2023学年高一上学期期中数学试题(已下线)2.2 基本不等式(第2课时)(分层作业)-【上好课】湖北省武汉市第四中学2023-2024学年高一上学期10月月考数学试题
19-20高一下·四川遂宁·期末
名校
5 . 首届世界低碳经济大会11月17日在南昌召开,本届大会的主题为“节能减排,绿色生态”.某企业在国家科研部门的支持下,投资810万元生产并经营共享单车,第一年维护费为10万元,以后每年增加20万元,每年收入租金300万元.
(1)若扣除投资和各种维护费,则从第几年开始获取纯利润?
(2)若干年后企业为了投资其他项目,有两种处理方案:
①纯利润总和最大时,以100万元转让经营权;
②年平均利润最大时以460万元转让经营权,问哪种方案更优?
(1)若扣除投资和各种维护费,则从第几年开始获取纯利润?
(2)若干年后企业为了投资其他项目,有两种处理方案:
①纯利润总和最大时,以100万元转让经营权;
②年平均利润最大时以460万元转让经营权,问哪种方案更优?
您最近一年使用:0次
2020-07-22更新
|
915次组卷
|
4卷引用:第03章不等式(B卷提升篇)-2020-2021学年高二数学必修五同步单元AB卷(人教A版,浙江专用)
(已下线)第03章不等式(B卷提升篇)-2020-2021学年高二数学必修五同步单元AB卷(人教A版,浙江专用)四川省遂宁市2019-2020学年高一下学期期末考试数学试题江苏省扬州市高邮中学2020-2021学年高二上学期10月联考数学试题江苏省连云港市2022-2023学年高一上学期期末模拟数学试题(5)
6 . 某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨.销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.
(1)列出甲、乙两种产品满足的关系式,并画出相应的平面区域;
(2)在一个生产周期内该企业生产甲、乙两种产品各多少吨时可获得利润最大,最大利润是多少?
(用线性规划求解要画出规范的图形及具体的解答过程)
(1)列出甲、乙两种产品满足的关系式,并画出相应的平面区域;
(2)在一个生产周期内该企业生产甲、乙两种产品各多少吨时可获得利润最大,最大利润是多少?
(用线性规划求解要画出规范的图形及具体的解答过程)
您最近一年使用:0次
2020-02-27更新
|
481次组卷
|
5卷引用:专题3.1二元一次不等式(组)与简单的线性规划问题(B卷提升篇)-2020-2021学年高二数学必修五同步单元AB卷(人教A版,浙江专用)
(已下线)专题3.1二元一次不等式(组)与简单的线性规划问题(B卷提升篇)-2020-2021学年高二数学必修五同步单元AB卷(人教A版,浙江专用)安徽省淮北市相山区师范大学附属实验中学2019-2020学年高二上学期期末数学(理)试题安徽省淮北市相山区淮北师范大学附属实验中学2019-2020学年高二上学期期末数学(文)试题宁夏石嘴山市第三中学2019-2020学年高二上学期第二次月考数学(文)试题安徽省黄山市屯溪第一中学2019-2020学年高一下学期入学考试数学试题
9-10高一下·河南郑州·阶段练习
7 . 某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如下表所示:
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
 产品 产品消耗量 资源 | 甲产品(每吨) | 乙产品(每吨) | 资源限额(每天) |
| 煤(t) | 9 | 4 | 360 |
| 电力(kw·h) | 4 | 5 | 200 |
| 劳动力(个) | 3 | 10 | 300 |
| 利润(万元) | 6 | 12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
您最近一年使用:0次
2016-11-30更新
|
1025次组卷
|
7卷引用:第03章不等式(A卷基础篇)-2020-2021学年高二数学必修五同步单元AB卷(人教A版,浙江专用)
(已下线)第03章不等式(A卷基础篇)-2020-2021学年高二数学必修五同步单元AB卷(人教A版,浙江专用)(已下线)第3章 章末检测(B)-2018-2019版数学创新设计课堂讲义同步系列(苏教版必修5)(已下线)河南省郑州盛同学校09-10学年下学期阶段测试2高一数学(已下线)2011届广东省华南师大附中高三综合检测数学理卷天津市河西区2017高三二模数学(文科)试题广西桂林市阳朔中学2017-2018学年高二10月月考文数试卷广西壮族自治区田阳高中2019-2020学年高一5月月考数学试题



