名校
1 . 在某公司举行的一次真假游戏的有奖竞猜中,设置了“科技”和“生活”这两类试题,规定每位职工最多竞猜3次,每次竞猜的结果相互独立.猜中一道“科技”类试题得4分,猜中一道“生活”类试题得2分,两类试题猜不中的都得0分.将职工得分逐次累加并用X表示,如果X的值不低于4分就认为通过游戏的竞猜,立即停止竞猜,否则继续竞猜,直到竞猜完3次为止.竞猜的方案有以下两种:方案1:先猜一道“科技”类试题,然后再连猜两道“生活”类试题;
方案2:连猜三道“生活”类试题.
设职工甲猜中一道“科技”类试题的概率为0.5,猜中一道“生活”类试题的概率为0.6.
(1)你认为职工甲选择哪种方案通过竞猜的可能性大?并说明理由.
(2)职工甲选择哪一种方案所得平均分高?并说明理由.
方案2:连猜三道“生活”类试题.
设职工甲猜中一道“科技”类试题的概率为0.5,猜中一道“生活”类试题的概率为0.6.
(1)你认为职工甲选择哪种方案通过竞猜的可能性大?并说明理由.
(2)职工甲选择哪一种方案所得平均分高?并说明理由.
您最近一年使用:0次
2019-04-26更新
|
1052次组卷
|
4卷引用:四川省兴文第二中学校2023-2024学年高三上学期2月期末理科数学试题
2 . “现值”与“终值”是利息计算中的两个基本概念,终值是现在的一笔钱按给定的利息率计算所得到的在未来某个时间点的价值。现值是未来的一笔钱按给定的利息率计算所得到的现在的价值。例如,在复利计息的情况下,设本金为A,每期利率为r,期数为n,到期末的本利和为S,则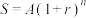 其中,S称为n期末的终值,A称为n期后终值S的现值,即n期后的S元现在的价值为
其中,S称为n期末的终值,A称为n期后终值S的现值,即n期后的S元现在的价值为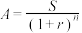 .现有如下问题:小明想买一套房子有如下两个方案
.现有如下问题:小明想买一套房子有如下两个方案
方案一:一次性付全款50万元;
方案二:分期付款,每年初付款6万元,第十年年初付完;
(1)已知一年期存款的年利率为4%,试讨论两种方案哪一种更好?
(2)若小明把房子租出去,第一年年初需交纳租金2万元,此后每年初涨租金1000元,假设存款的年利率为4%,预计第十年房租到期后小明所获得全部租金的终值.(精确到百元).参考数据:
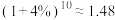 .
.
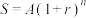 其中,S称为n期末的终值,A称为n期后终值S的现值,即n期后的S元现在的价值为
其中,S称为n期末的终值,A称为n期后终值S的现值,即n期后的S元现在的价值为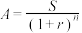 .现有如下问题:小明想买一套房子有如下两个方案
.现有如下问题:小明想买一套房子有如下两个方案方案一:一次性付全款50万元;
方案二:分期付款,每年初付款6万元,第十年年初付完;
(1)已知一年期存款的年利率为4%,试讨论两种方案哪一种更好?
(2)若小明把房子租出去,第一年年初需交纳租金2万元,此后每年初涨租金1000元,假设存款的年利率为4%,预计第十年房租到期后小明所获得全部租金的终值.(精确到百元).参考数据:
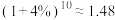 .
.
您最近一年使用:0次
2023-10-29更新
|
350次组卷
|
3卷引用:河南省郑州市宇华实验学校2024届高三上学期期末数学试题
河南省郑州市宇华实验学校2024届高三上学期期末数学试题山东省济南市莱芜第一中学2023-2024学年高三上学期10月月考数学试题(已下线)1.4 数列在日常经济生活中的应用4种常见考法归类-【帮课堂】2023-2024学年高二数学同步学与练(北师大版2019选择性必修第二册)
3 . 某学校进行趣味投篮比赛,设置了A,B两种投篮方案.方案A:罚球线投篮,投中可以得2分,投不中得0分;方案B:三分线外投篮,投中可以得3分,投不中得0分.甲、乙两位员工参加比赛,选择方案A投中的概率都为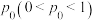 ,选择方案B投中的概率都为
,选择方案B投中的概率都为 ,每人有且只有一次投篮机会,投中与否互不影响.
,每人有且只有一次投篮机会,投中与否互不影响.
(1)若甲选择方案A投篮,乙选择方案B投篮,记他们的得分之和为X,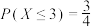 ,求X的分布列;
,求X的分布列;
(2)若甲、乙两位员工都选择方案A或都选择方案B投篮,问:他们都选择哪种方案投篮,得分之和的均值较大?
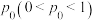 ,选择方案B投中的概率都为
,选择方案B投中的概率都为 ,每人有且只有一次投篮机会,投中与否互不影响.
,每人有且只有一次投篮机会,投中与否互不影响.(1)若甲选择方案A投篮,乙选择方案B投篮,记他们的得分之和为X,
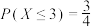 ,求X的分布列;
,求X的分布列;(2)若甲、乙两位员工都选择方案A或都选择方案B投篮,问:他们都选择哪种方案投篮,得分之和的均值较大?
您最近一年使用:0次
23-24高三上·山东·阶段练习
4 . 某班级为了提高学习数学、物理的兴趣,组织了一次答题比赛活动,规定每位学生共需回答3道题目.现有两种方案供学生任意选择,甲方案:只选数学问题;乙方案:第一次选数学问题,以后按如下规则选题,若本次回答正确,则下一次选数学问题,若回答错误,则下一次选物理问题.数学问题中的每个问题回答正确得50分,否则得0分;物理问题中的每个问题回答正确得30分,否则得0分.已知A同学能正确回答数学问题的概率为 ,能正确回答物理问题的概率为
,能正确回答物理问题的概率为 ,且能正确回答问题的概率与回答顺序无关.
,且能正确回答问题的概率与回答顺序无关.
(1)求A同学采用甲方案答题,得分不低于100分的概率;
(2)A同学选择哪种方案参加比赛更加合理,并说明理由.
 ,能正确回答物理问题的概率为
,能正确回答物理问题的概率为 ,且能正确回答问题的概率与回答顺序无关.
,且能正确回答问题的概率与回答顺序无关.(1)求A同学采用甲方案答题,得分不低于100分的概率;
(2)A同学选择哪种方案参加比赛更加合理,并说明理由.
您最近一年使用:0次
2023·全国·模拟预测
解题方法
5 . 为了响应政府号召,增加农民收入,某村委会指导当地村民在果园里进行生态鸡的养殖,在2023年8月初,为了解所养殖的生态鸡的质量(单位;kg)情况,养殖负责人随机抓取了一部分鸡进行称重,得到如下频率分布直方图(同一组中的数据用该组区间的中点值代替),以样本估计总体.

(1)求养殖的生态鸡的质量的平均值.
(2)该地现养殖有5000只鸡,为了减轻养殖的压力,养殖负责人计划卖掉一部分鸡,另一部分计划春节再卖掉.若现在卖掉,价格为20元/kg,到春节卖掉,预估价格为22元/kg.现有以下两种方案:
方案一:体重不低于2.5kg的现在卖掉,其余的养殖到春节再卖掉,剩余的鸡平均每只需要10元养殖费用,到春节时,平均质量可以达到2.5kg;
方案二:体重不低于2kg的现在卖掉,其余的养殖到春节再卖掉,剩余的鸡平均每只需要10元养殖费用,到春节时,平均质量可以达到3kg.
从经济收益的角度来看,选择哪种方案更合适?

(1)求养殖的生态鸡的质量的平均值.
(2)该地现养殖有5000只鸡,为了减轻养殖的压力,养殖负责人计划卖掉一部分鸡,另一部分计划春节再卖掉.若现在卖掉,价格为20元/kg,到春节卖掉,预估价格为22元/kg.现有以下两种方案:
方案一:体重不低于2.5kg的现在卖掉,其余的养殖到春节再卖掉,剩余的鸡平均每只需要10元养殖费用,到春节时,平均质量可以达到2.5kg;
方案二:体重不低于2kg的现在卖掉,其余的养殖到春节再卖掉,剩余的鸡平均每只需要10元养殖费用,到春节时,平均质量可以达到3kg.
从经济收益的角度来看,选择哪种方案更合适?
您最近一年使用:0次
2023·河南·模拟预测
名校
解题方法
6 . 某公司为了让职工业余时间加强体育锻炼,修建了一个运动俱乐部,公司随机抽查了200名职工在修建运动俱乐部前后每天运动的时间,得到以下频数分布表:
表一(运动俱乐部修建前)
表二(运动俱乐部修建后)
(1)分别求出修建运动俱乐部前和修建运动俱乐部后职工每天运动的平均时间(同一时间段的数据取该组区间的中点值作代表)﹔
(2)运动俱乐部内有一套与室温调节有关的设备,内有2个完全一样的用电器A,只有这2个用电器A都正常工作时,整套设备才正常工作,且2个用电器A是否正常工作互不影响.用电器A有M,N两种品牌,M品牌的销售单价为1000元,正常工作寿命为11个月或12个月(概率均为 );N品牌的销售单价为400元,正常工作寿命为5个月或6个月(概率均为
);N品牌的销售单价为400元,正常工作寿命为5个月或6个月(概率均为 ).现有两种购置方案:
).现有两种购置方案:
方案1:购置2个M品牌用电器﹔
方案2:购置1个M品牌用电器和2个N品牌用电器(其中1个N品牌用电器不能正常工作时则使用另一个N品牌用电器).
试求两种方案各自设备性价比(设备正常运行时间与购置用电器A的成本比)的分布列,并从性价比的数学期望角度考虑,选择哪种方案更实惠?
表一(运动俱乐部修建前)
| 时间(分钟) |  |  | 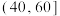 | 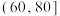 |
| 人数 | 36 | 58 | 81 | 25 |
| 时间(分钟) |  |  | 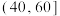 | 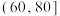 |
| 人数 | 18 | 63 | 83 | 36 |
(2)运动俱乐部内有一套与室温调节有关的设备,内有2个完全一样的用电器A,只有这2个用电器A都正常工作时,整套设备才正常工作,且2个用电器A是否正常工作互不影响.用电器A有M,N两种品牌,M品牌的销售单价为1000元,正常工作寿命为11个月或12个月(概率均为
 );N品牌的销售单价为400元,正常工作寿命为5个月或6个月(概率均为
);N品牌的销售单价为400元,正常工作寿命为5个月或6个月(概率均为 ).现有两种购置方案:
).现有两种购置方案:方案1:购置2个M品牌用电器﹔
方案2:购置1个M品牌用电器和2个N品牌用电器(其中1个N品牌用电器不能正常工作时则使用另一个N品牌用电器).
试求两种方案各自设备性价比(设备正常运行时间与购置用电器A的成本比)的分布列,并从性价比的数学期望角度考虑,选择哪种方案更实惠?
您最近一年使用:0次
2023-05-19更新
|
525次组卷
|
5卷引用:模块三 专题7 大题分类练(概率)基础夯实练
22-23高二下·福建南平·期末
7 . 某公司举办公司员工联欢晩会,为活跃气氛,计划举行摸奖活动,有两种方案:
方案一:不放回从装有 个红球和
个红球和 个白球的箱子中随机摸出
个白球的箱子中随机摸出 个球,每摸出一红球奖励
个球,每摸出一红球奖励 元:
元:
方案二:有放回从装有 个红球和
个红球和 个白球的箱子中随机摸出
个白球的箱子中随机摸出 个球,每摸出一红球奖励
个球,每摸出一红球奖励 元,分别用随机变量
元,分别用随机变量 、
、 表示某员工按方案一和方案二抽奖的获奖金额.
表示某员工按方案一和方案二抽奖的获奖金额.
(1)求随机变量 的分布列和数学期望:
的分布列和数学期望:
(2)用统计知识分析,为使公司员工获奖金额相对均衡,应选择哪种方案?请说明理由.
方案一:不放回从装有
 个红球和
个红球和 个白球的箱子中随机摸出
个白球的箱子中随机摸出 个球,每摸出一红球奖励
个球,每摸出一红球奖励 元:
元:方案二:有放回从装有
 个红球和
个红球和 个白球的箱子中随机摸出
个白球的箱子中随机摸出 个球,每摸出一红球奖励
个球,每摸出一红球奖励 元,分别用随机变量
元,分别用随机变量 、
、 表示某员工按方案一和方案二抽奖的获奖金额.
表示某员工按方案一和方案二抽奖的获奖金额.(1)求随机变量
 的分布列和数学期望:
的分布列和数学期望:(2)用统计知识分析,为使公司员工获奖金额相对均衡,应选择哪种方案?请说明理由.
您最近一年使用:0次
名校
解题方法
8 . 为了预防某种流感扩散,某校医务室采取积极的处理方式,对感染者进行短暂隔离直到康复.假设某班级已知6位同学中有1位同学被感染,需要通过化验血液来确定被感染的同学,血液化验结果呈阳性即被感染,呈阴性即未被感染.下面是两种化验方案.
方法甲:逐个化验,直到能确定被感染的同学为止.
方案乙:先任取3个同学,将他们的血液混在一起化验,若结果呈阳性则表明被感染同学为这3位中的1位,后再逐个化验,直到能确定被感染的同学为止;若结果呈阴性,则在另外3位同学中逐个检测.
(1)求方案甲所需化验次数等于方案乙所需化验次数的概率;
(2) 表示方案甲所需化验次数,
表示方案甲所需化验次数, 表示方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑哪种化验的方案最佳.
表示方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑哪种化验的方案最佳.
方法甲:逐个化验,直到能确定被感染的同学为止.
方案乙:先任取3个同学,将他们的血液混在一起化验,若结果呈阳性则表明被感染同学为这3位中的1位,后再逐个化验,直到能确定被感染的同学为止;若结果呈阴性,则在另外3位同学中逐个检测.
(1)求方案甲所需化验次数等于方案乙所需化验次数的概率;
(2)
 表示方案甲所需化验次数,
表示方案甲所需化验次数, 表示方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑哪种化验的方案最佳.
表示方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑哪种化验的方案最佳.
您最近一年使用:0次
2020-04-30更新
|
140次组卷
|
6卷引用:山西省晋城市第一中学校2023-2024学年高三上学期第十二次调研考试数学试题
山西省晋城市第一中学校2023-2024学年高三上学期第十二次调研考试数学试题【全国市级联考】安徽省芜湖市2018届高三5月模拟考试理科数学试题甘肃省师大附中2017-2018学年下学期高二期末模拟理科数学试卷 (选修2-2 2-3)【全国百强校】湖南省岳阳市第一中学2019届高三第一次模拟(5月)数学(理)试题西藏拉萨中学2019-2020学年高三第六次月考数学(理)试题(已下线)第七章 随机变量及其分布 (单元测试)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第三册)
名校
9 . 最优化原理是指要求目前存在的多种可能的方案中,选出最合理的,达到事先规定的最优目标的方案,这类问题称之为最优化问题.为了解决实际生活中的最优化问题,我们常常需要在数学模型中求最大值或者最小值.下面是一个有关曲线与直线上点的距离的最值问题,请你利用所学知识来解答:若点 是曲线
是曲线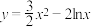 上任意一点,则
上任意一点,则 到直线
到直线 的距离的最小值为( )
的距离的最小值为( )
 是曲线
是曲线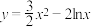 上任意一点,则
上任意一点,则 到直线
到直线 的距离的最小值为( )
的距离的最小值为( )A.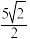 | B. | C. | D.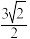 |
您最近一年使用:0次
2024-02-14更新
|
840次组卷
|
3卷引用:山东省聊城市2024届高三上学期期末教学质量检测数学试题
山东省聊城市2024届高三上学期期末教学质量检测数学试题(已下线)2.4导数的四则运算法则(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)广东省东莞市光明中学2023-2024学年高二下学期第一次月考数学试题
解题方法
10 . 2023年杭州亚运会的吉祥物包括三种机器人造型,分别名叫“莲莲”,“琮琮”“宸宸”,小辉同学将三种吉祥物各购买了两个(同名的两个吉祥物完全相同),送给三位好朋友,每人两个,则每个好朋友都收到不同名的吉祥物的分配方案共有____________ 种.(用数字作答)
您最近一年使用:0次



