1 . 对于函数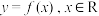 及给定的实数
及给定的实数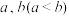 ,若存在正实数t使得函数
,若存在正实数t使得函数 在区间
在区间 和
和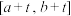 上同为增函数或同为减函数,则称函数
上同为增函数或同为减函数,则称函数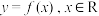 为区间
为区间 上的
上的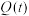 函数;
函数;
(1)已知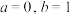 ,请指出函数
,请指出函数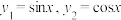 是否为区间[0,1]上的
是否为区间[0,1]上的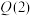 函数(不需要说明理由);
函数(不需要说明理由);
(2)已知 ,且函数
,且函数 是区间
是区间 上 的
上 的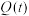 函数,请写出t的所有取值,并说明理由;
函数,请写出t的所有取值,并说明理由;
(3)若函数 既是区间
既是区间 上的
上的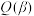 函数又是区间
函数又是区间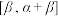 上的
上的 函数,当α、β取遍所有可取的值时,求出
函数,当α、β取遍所有可取的值时,求出 的取值范围.
的取值范围.
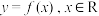 及给定的实数
及给定的实数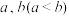 ,若存在正实数t使得函数
,若存在正实数t使得函数 在区间
在区间 和
和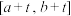 上同为增函数或同为减函数,则称函数
上同为增函数或同为减函数,则称函数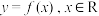 为区间
为区间 上的
上的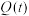 函数;
函数;(1)已知
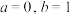 ,请指出函数
,请指出函数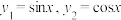 是否为区间[0,1]上的
是否为区间[0,1]上的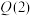 函数(不需要说明理由);
函数(不需要说明理由);(2)已知
 ,且函数
,且函数 是区间
是区间 上 的
上 的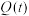 函数,请写出t的所有取值,并说明理由;
函数,请写出t的所有取值,并说明理由;(3)若函数
 既是区间
既是区间 上的
上的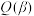 函数又是区间
函数又是区间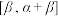 上的
上的 函数,当α、β取遍所有可取的值时,求出
函数,当α、β取遍所有可取的值时,求出 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
2 . 已知函数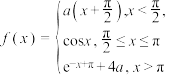 给出下列四个结论:
给出下列四个结论:
①若 有最小值,则
有最小值,则 的取值范围是
的取值范围是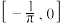 ;
;
②当 时,若
时,若 无实根,则
无实根,则 的取值范围是
的取值范围是 ;
;
③当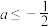 时,不等式
时,不等式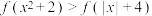 的解集为
的解集为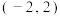 ;
;
④当 时,若存在
时,若存在 ,满足
,满足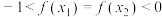 ,则
,则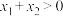 .
.
其中,所有正确结论的序号为__________ .
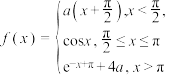 给出下列四个结论:
给出下列四个结论:①若
 有最小值,则
有最小值,则 的取值范围是
的取值范围是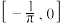 ;
;②当
 时,若
时,若 无实根,则
无实根,则 的取值范围是
的取值范围是 ;
;③当
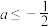 时,不等式
时,不等式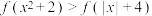 的解集为
的解集为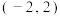 ;
;④当
 时,若存在
时,若存在 ,满足
,满足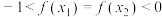 ,则
,则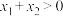 .
.其中,所有正确结论的序号为
您最近一年使用:0次
2023-11-02更新
|
1154次组卷
|
6卷引用:北京市第一零一中学2024届高三上学期10月月考数学试题
名校
3 . 记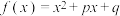 (
( ),
),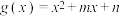 (
(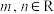 ).
).
(1)若 的解集为
的解集为 ,求
,求 和
和 的值;
的值;
(2)若方程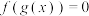 和
和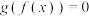 都没有实数根,求证:方程
都没有实数根,求证:方程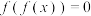 和
和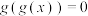 至少有一个没有实数根;
至少有一个没有实数根;
(3)若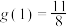 ,对任意的
,对任意的 ,都存在
,都存在 使得关于
使得关于 的不等式
的不等式 有解,求实数
有解,求实数 的取值范围.
的取值范围.
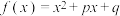 (
( ),
),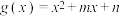 (
(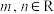 ).
).(1)若
 的解集为
的解集为 ,求
,求 和
和 的值;
的值;(2)若方程
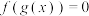 和
和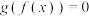 都没有实数根,求证:方程
都没有实数根,求证:方程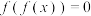 和
和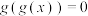 至少有一个没有实数根;
至少有一个没有实数根;(3)若
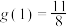 ,对任意的
,对任意的 ,都存在
,都存在 使得关于
使得关于 的不等式
的不等式 有解,求实数
有解,求实数 的取值范围.
的取值范围.
您最近一年使用:0次



