1 . 证明下列等式:
(1)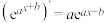 ;
;
(2)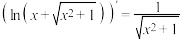 .
.
(1)
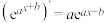 ;
;(2)
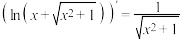 .
.
您最近一年使用:0次
解题方法
2 . 证明:函数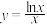 在区间
在区间 上是严格增函数.
上是严格增函数.
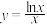 在区间
在区间 上是严格增函数.
上是严格增函数.
您最近一年使用:0次
22-23高二下·全国·课后作业
解题方法
3 . 已知函数 ,求证
,求证 恒成立.
恒成立.
 ,求证
,求证 恒成立.
恒成立.
您最近一年使用:0次
23-24高二上·吉林长春·期末
名校
解题方法
4 . 已知函数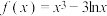 .
.
(1)求 的最小值;
的最小值;
(2)设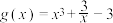 ,证明:
,证明:
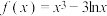 .
.(1)求
 的最小值;
的最小值;(2)设
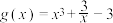 ,证明:
,证明:
您最近一年使用:0次
2024-01-10更新
|
2489次组卷
|
16卷引用:吉林省长春市长春吉大附中实验学校2023-2024学年高二上学期1月期末数学试题
(已下线)吉林省长春市长春吉大附中实验学校2023-2024学年高二上学期1月期末数学试题(已下线)专题10 导数12种常见考法归类(3)(已下线)第五章 一元函数的导数及其应用(单元测试)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第二册)(已下线)第5.3.2讲 利用导数求解函数的综合问题(第3课时)-2023-2024学年高二数学同步精讲精练宝典(人教A版2019选修第二、三册)(已下线)第五章 一元函数的导数及其应用章末综合达标卷-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第二、三册)(已下线)第六章:导数及其应用(单元测试)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第三册)(已下线)专题4 导数在不等式中的应用(讲)山东省临沂市兰山区临沂商城外国语学校2023-2024学年高二下学期3月月考数学试题山东省威海市乳山市银滩高级中学2023-2024学年高二下学期3月月考数学试题(已下线)导数专题:导数与不等式成立问题(6大题型)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第二册)(已下线)第二章 导数及其应用(单元综合检测卷)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)广东省东莞市常平中学2023-2024学年高二下学期3月阶段检测数学试题(已下线)模块一 专题4 《导数在不等式中的应用》(苏教版)广东省中山市2023-2024学年高二下学期期末统一考试数学试卷(已下线)模型9 利用导数证明不等式问题模型(第5章 一元函数的导数及其应用)山东省枣庄市滕州市第五中学2025届高三上学期第一次单元检测(10月月考)数学试题
2024高三·全国·专题练习
解题方法
5 . 已知函数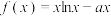 ,证明:对一切
,证明:对一切 ,都有
,都有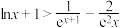 成立.
成立.
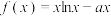 ,证明:对一切
,证明:对一切 ,都有
,都有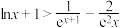 成立.
成立.
您最近一年使用:0次
6 . 已知函数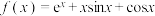 ,
, .
.
(1)求曲线 在点
在点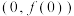 处的切线方程;
处的切线方程;
(2)证明: 在
在 上单调递增.
上单调递增.
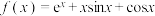 ,
, .
.(1)求曲线
 在点
在点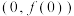 处的切线方程;
处的切线方程;(2)证明:
 在
在 上单调递增.
上单调递增.
您最近一年使用:0次
2023-12-19更新
|
843次组卷
|
3卷引用:江苏省决胜新高考2024届高三上学期12月大联考数学试题
江苏省决胜新高考2024届高三上学期12月大联考数学试题(已下线)第五章 一元函数的导数及其应用(单元综合测试卷)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)河南省信阳市浉河区信阳高级中学2023-2024学年高二下学期6月月考数学试题
解题方法
7 . 证明: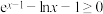 .
.
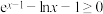 .
.
您最近一年使用:0次
8 . 求证:当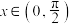 时,
时, .
.
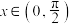 时,
时, .
.
您最近一年使用:0次
2021高三·全国·专题练习
解题方法
9 . 已知函数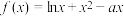 .
.
(1)若函数 在定义域内为增函数,求实数
在定义域内为增函数,求实数 的取值范围;
的取值范围;
(2)若 且
且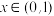 ,求证:
,求证: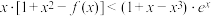 .
.
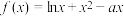 .
.(1)若函数
 在定义域内为增函数,求实数
在定义域内为增函数,求实数 的取值范围;
的取值范围;(2)若
 且
且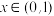 ,求证:
,求证: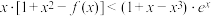 .
.
您最近一年使用:0次

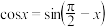 ,
,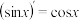 ,证明:
,证明: .
.


