2024高一上·江苏·专题练习
解题方法
1 . 已知函数 是定义在
是定义在 上的单调函数,且对
上的单调函数,且对 都有
都有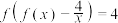 ,则
,则
______ .
 是定义在
是定义在 上的单调函数,且对
上的单调函数,且对 都有
都有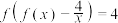 ,则
,则
您最近一年使用:0次
名校
解题方法
2 . 函数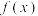 满足若
满足若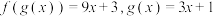 ,则
,则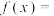 ( )
( )
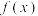 满足若
满足若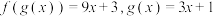 ,则
,则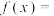 ( )
( )A.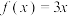 | B.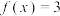 |
C.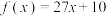 | D.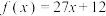 |
您最近一年使用:0次
2024-06-29更新
|
2556次组卷
|
11卷引用:5.2 函数的表示方法-【题型分类归纳】(苏教版2019必修第一册)
(已下线)5.2 函数的表示方法-【题型分类归纳】(苏教版2019必修第一册)(已下线)热点专题 2-1 函数的基本概念及其性质(解析式,定义域,值域)-1(已下线)专题1 函数解析式的求法 (精细化解析)(已下线)核心考点4 函数的三要素 考点讲解 (高一期中考试必考的7大核心考点)湖南省衡阳市祁东县育贤中学2023-2024学年高一上学期期中数学试题(已下线)【第一练】3.1.2函数的表示法湖北省黄冈市浠水县第一中学2023-2024学年高一上学期期中数学试题(已下线)专题03 函数的概念与性质1-2024年高一数学寒假作业单元合订本(已下线)专题拓展:函数解析式的常见求法-【暑假自学课】(人教A版2019必修第一册)(已下线)第10讲 函数及其表示方法-【暑假自学课】(人教B版2019必修第一册)广东省深圳市桃源居中澳实验学校(港澳台基础班)2025届高三上学期九月调研考试数学试题
3 . 已知函数 ,且
,且 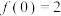 ,
, 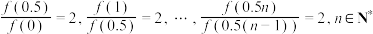 ,则函数
,则函数 的一个解析式为
的一个解析式为____________ .
 ,且
,且 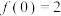 ,
, 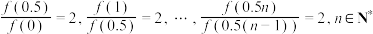 ,则函数
,则函数 的一个解析式为
的一个解析式为
您最近一年使用:0次
2024-01-02更新
|
839次组卷
|
8卷引用:5.2 函数的表示方法(1)-【帮课堂】(苏教版2019必修第一册)
(已下线)5.2 函数的表示方法(1)-【帮课堂】(苏教版2019必修第一册)(已下线)5.2 函数的表示方法(1)(已下线)重难点突破01 抽象函数模型归纳总结(八大题型)(已下线)第01讲 函数的概念及其表示(十六大题型)(讲义)-2(已下线)第13讲 函数的表示方法(1)-【暑假自学课】(苏教版2019必修第一册)湖北省智学联盟2021-2022学年高一上学期12月联考数学试题湖北省老河口市第一中学2023-2024学年高一数学上学期期末复习题【课后练】 4.2.1 指数爆炸和指数衰减 课后作业-湘教版(2019)必修(第一册) 第4章 幂函数、指数函数和对数函数
解题方法
4 . 已知函数 对任意实数
对任意实数 都有
都有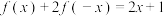 ,则
,则
_______ .
 对任意实数
对任意实数 都有
都有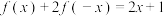 ,则
,则
您最近一年使用:0次
名校
解题方法
5 . 已知函数 满足
满足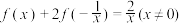 ,则函数
,则函数 的解析式为
的解析式为___________ .
 满足
满足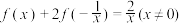 ,则函数
,则函数 的解析式为
的解析式为
您最近一年使用:0次
2023-11-22更新
|
831次组卷
|
5卷引用:5.2 函数的表示方法-【题型分类归纳】(苏教版2019必修第一册)
(已下线)5.2 函数的表示方法-【题型分类归纳】(苏教版2019必修第一册)(已下线)第13讲 函数的表示方法(1)-【暑假自学课】(苏教版2019必修第一册)安徽省阜阳市临泉第一中学等鼎尖教育2023-2024学年高一上学期11月联考数学试题重庆市部分学校2023-2024学年高一上学期期中数学试题(已下线)专题拓展:函数解析式的常见求法-【暑假自学课】(人教A版2019必修第一册)
名校
解题方法
6 . 已知 ,则
,则
______ .
 ,则
,则
您最近一年使用:0次
解题方法
7 . 已知函数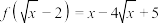 ,则
,则 的解析式为( )
的解析式为( )
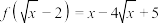 ,则
,则 的解析式为( )
的解析式为( )A.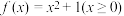 | B.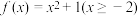 |
C. | D.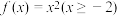 |
您最近一年使用:0次
2023-11-16更新
|
1500次组卷
|
7卷引用:5.2 函数的表示方法-【题型分类归纳】(苏教版2019必修第一册)
(已下线)5.2 函数的表示方法-【题型分类归纳】(苏教版2019必修第一册)(已下线)第13讲 函数的表示方法(2)-【暑假自学课】(苏教版2019必修第一册)浙江省“七彩阳光”新高考研究联盟2023-2024学年高一上学期期中检测数学试题 (已下线)专题03 函数的概念与幂函数2-期末复习重难培优与单元检测(人教A版2019)(已下线)专题03 函数的概念与幂函数1 -期末复习重难培优与单元检测(人教A版2019)(已下线)专题拓展:函数解析式的常见求法-【暑假自学课】(人教A版2019必修第一册)【课后练】 3.1.2 表示函数的方法+3.1.3 简单的分段函数 课后作业-湘教版(2019)必修(第一册)第3章 函数的概念与性质
10-11高二下·辽宁大连·期末
名校
解题方法
8 . 已知二次函数 满足条件
满足条件 ,且
,且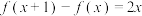 .
.
(1)求函数 的解析式;
的解析式;
(2)在区间 上,
上, 的图象恒在
的图象恒在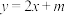 的图象上方,求实数
的图象上方,求实数 的取值范围.
的取值范围.
 满足条件
满足条件 ,且
,且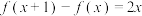 .
.(1)求函数
 的解析式;
的解析式;(2)在区间
 上,
上, 的图象恒在
的图象恒在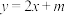 的图象上方,求实数
的图象上方,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-11-15更新
|
881次组卷
|
48卷引用:专题06 二次函数与一元二次方程、不等式-2021届江苏省新高考数学大讲坛大一轮复习
(已下线)专题06 二次函数与一元二次方程、不等式-2021届江苏省新高考数学大讲坛大一轮复习沪教版(上海) 高三年级 新高考辅导与训练 第一章 集合与函数 本章测试(已下线)专题2.4 二次函数与幂函数(精测)-2021届高考数学(理)一轮复习讲练测(已下线)专题2.4 二次函数与幂函数(精练)-2021年高考数学(文)一轮复习学与练(已下线)专题2.4 二次函数与幂函数(精练)-2021年高考数学(理)一轮复习学与练(已下线)专题2.4 二次函数与幂函数(精测)-2021届高考数学(文)一轮复习讲练测(已下线)专题2.4 二次函数与幂函数(精练)-2021届高考数学(文)一轮复习讲练测(已下线)测试卷03 基本初等函数(A)-2021届高考数学一轮复习(文理通用)单元过关测试卷(已下线)课时12 函数的概念、函数关系及运算-2022年高考数学一轮复习小题多维练(上海专用)(已下线)第03讲 函数及其性质- 1江苏省南京市2023-2024学年高一上学期期中复习数学试题江苏省南京市2023-2024学年高一上学期期末考前模拟数学试题(已下线)3.1.2函数的表示法(第1课时)(已下线)2.4 二次函数(高三一轮)【同步课时】基础卷(已下线)2010-2011年辽宁省瓦房店市高级中学高二下学期期末联考文科数学宁夏长庆高级中学2020届高三上学期第一次月考数学(理)试卷上海市浦东新区浦东外国语学校2018-2019学年高一上学期12月月考数学试题江西省宜春市丰城市丰城九中2018-2019学年高一上学期期末数学试题广西南宁市第三中学2019-2020学年高一上学期期中数学试题新疆哈密市第十五中学2019-2020学年高一上学期期中数学试题陕西省延安市黄陵中学高新部2019-2020学年高一上学期期中数学试题宁夏吴忠市青铜峡市高级中学2019-2020学年高一上学期期中数学试题辽宁省鞍山市台安县高级中学2019-2020学年高一上学期期中数学试题湖南省怀化市2016-2017学年高一上学期期末数学试题宁夏六盘山高级中学2018-2019学年高二下学期期末测数学(文)试题甘肃省兰州市第二中学2019-2020学年高一上学期期中考试数学试题河北省深州市长江中学2020届高三上学期期中数学(理)试题(已下线)专题17函数的概念与解析式、函数的运算- 2020年初升高数学无忧衔接(沪教版)陕西省咸阳市永寿县中学2020-2021学年高一上学期第一次月考数学试题安徽省阜阳市界首中学2020-2021学年高一上学期10月月考数学试题(A卷)安徽省合肥市肥东县高级中学2020-2021学年高三上学期期中数学(文)试题新疆北屯高级中学2020-2021学年高一10月月考数学试题北京市第四十三中学2020-2021学年高一12月月考数学试题江西省靖安中学2020-2021学年高一上学期第二次月考数学试题湖北省武汉市经济技术开发区第一中学2021-2022学年高一上学期第一次月考数学试题黑龙江省漠河市高级中学2021-2022学年高一上学期第一次月考数学试题河北省保定市定州市2021-2022学年高一上学期期中数学试题广东省揭阳市普宁市普师高级中学2021-2022学年高一上学期期中数学试题河北正中实验中学2021-2022学年高一上学期期中数学试题山东省潍坊第四中学2021-2022学年高三上学期开学考试数学试题甘肃省金昌市永昌县第一高级中学2020-2021学年高一上学期第一次月考数学试题黑龙江省牡丹江市第三高级中学2022-2023学年高三上学期第一次月考数学试题黑龙江省牡丹江市第二高级中学2021-2022学年高二下学期期末考试数学试题广东省阳江市江城北中学2022-2023学年高一上学期期中数学试题广东省江门市新会陈经纶中学2023届高三上学期8月月考数学试题第三章 函数的概念与性质 (B卷·提升能力)海南省海口市第一中学2022-2023学年高一上学期期中检测数学试题(已下线)3.1.2函数的表示法——课后作业(巩固版)
解题方法
9 . 已知函数 是一次函数,满足
是一次函数,满足 ,则
,则 的解析式可能为( )
的解析式可能为( )
 是一次函数,满足
是一次函数,满足 ,则
,则 的解析式可能为( )
的解析式可能为( )A. | B. |
C. | D. |
您最近一年使用:0次
名校
解题方法
10 . 2023年10月11日,连接贵阳至广州的贵广高铁正式提速,按最高时速300公里运营,并同步加密列车开行频次,我国西南地区至珠三角及粤港澳大湾区的高铁运行时间进一步压缩.目前,铁路部门将在贵广高铁线路上开行列车177列,根据客流变化在高峰时段增加高峰线12列;其中,贵阳站至广州南站130列.贵广高铁提速将有效提升高铁运输能力和效率,对密切西南与华南地区往来交流、推动成渝地区双城经济圈和粤港澳大湾区高质量发展具有重要意义.
现在已知列车的发车时间间隔 (单位:分钟)满足
(单位:分钟)满足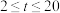 .经市场调研测算,列车载客量与发车时间间隔
.经市场调研测算,列车载客量与发车时间间隔 相关,当
相关,当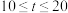 时列车为满载状态,载客量为720人;当
时列车为满载状态,载客量为720人;当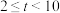 时,载客量会减少,减少的人数与
时,载客量会减少,减少的人数与 的平方成正比,且发车时间间隔为3分钟时的载客量为396人.记列车载客量为
的平方成正比,且发车时间间隔为3分钟时的载客量为396人.记列车载客量为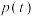 .
.
(1)求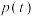 的表达式;
的表达式;
(2)若该线路每分钟的净收益为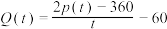 (元),问当发车时间间隔为多少时,该线路每分钟的净收益最大,并求出最大值.
(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大,并求出最大值.
现在已知列车的发车时间间隔
 (单位:分钟)满足
(单位:分钟)满足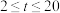 .经市场调研测算,列车载客量与发车时间间隔
.经市场调研测算,列车载客量与发车时间间隔 相关,当
相关,当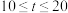 时列车为满载状态,载客量为720人;当
时列车为满载状态,载客量为720人;当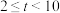 时,载客量会减少,减少的人数与
时,载客量会减少,减少的人数与 的平方成正比,且发车时间间隔为3分钟时的载客量为396人.记列车载客量为
的平方成正比,且发车时间间隔为3分钟时的载客量为396人.记列车载客量为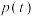 .
.(1)求
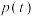 的表达式;
的表达式;(2)若该线路每分钟的净收益为
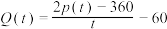 (元),问当发车时间间隔为多少时,该线路每分钟的净收益最大,并求出最大值.
(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大,并求出最大值.
您最近一年使用:0次



