名校
1 . 已知函数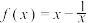
(1)判断函数 的奇偶性;
的奇偶性;
(2)根据定义证明函数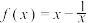 在区间
在区间 上单调递增..
上单调递增..
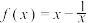
(1)判断函数
 的奇偶性;
的奇偶性;(2)根据定义证明函数
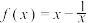 在区间
在区间 上单调递增..
上单调递增..
您最近一年使用:0次
2023-09-06更新
|
567次组卷
|
5卷引用:贵州省贵阳市普通中学2023-2024学年高一上学期期末监测考试数学试卷
贵州省贵阳市普通中学2023-2024学年高一上学期期末监测考试数学试卷广东省东莞市七校联考2022-2023学年高一上学期期中数学试题(已下线)4.1函数的奇偶性(分层练习,六大题型)-高一数学同步精品课堂(北师大版2019必修第一册)广东省惠州市龙门县高级中学2023-2024学年高一上学期期中考试数学试题四川省眉山市彭山区第一中学2023-2024学年高一下学期开学考试数学试题
解题方法
2 . 已知函数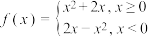 ,
, ,若
,若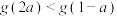 ,则实数
,则实数 的取值范围为( )
的取值范围为( )
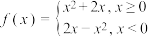 ,
, ,若
,若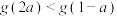 ,则实数
,则实数 的取值范围为( )
的取值范围为( )A. | B.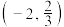 | C.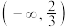 | D. |
您最近一年使用:0次
2023-07-28更新
|
424次组卷
|
2卷引用:贵州省贵阳市白云区第二高级中学2021-2022学年高二下学期期末联考数学(文)试题
解题方法
3 . 已知函数 是
是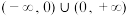 上的偶函数,当
上的偶函数,当 时,
时, .
.
(1)用单调性定义证明函数 在
在 上单调递增;
上单调递增;
(2)求当 时,函数的解析式.
时,函数的解析式.
 是
是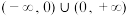 上的偶函数,当
上的偶函数,当 时,
时, .
.(1)用单调性定义证明函数
 在
在 上单调递增;
上单调递增;(2)求当
 时,函数的解析式.
时,函数的解析式.
您最近一年使用:0次
解题方法
4 . 历史上第一个给出函数一般定义的是19世纪数学家秋利克需(Dirichlet),他是最早倡导严格化方法的数学家之一,狄利克雷在1829年给出了著名的狄利克雷函数: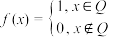 (Q是有理数集),狄利克雷函数的出现表示数学家们对数学的理解发生了深刻的变化,从研究“算”转变到了研究“概念、性质、结构”.一般地,广文的秋利克雷函数可以定义为:
(Q是有理数集),狄利克雷函数的出现表示数学家们对数学的理解发生了深刻的变化,从研究“算”转变到了研究“概念、性质、结构”.一般地,广文的秋利克雷函数可以定义为: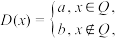 (其中
(其中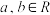 ,且
,且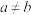 ).以下对
).以下对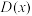 说法正确的有( )
说法正确的有( )
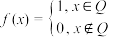 (Q是有理数集),狄利克雷函数的出现表示数学家们对数学的理解发生了深刻的变化,从研究“算”转变到了研究“概念、性质、结构”.一般地,广文的秋利克雷函数可以定义为:
(Q是有理数集),狄利克雷函数的出现表示数学家们对数学的理解发生了深刻的变化,从研究“算”转变到了研究“概念、性质、结构”.一般地,广文的秋利克雷函数可以定义为: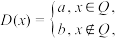 (其中
(其中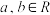 ,且
,且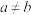 ).以下对
).以下对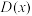 说法正确的有( )
说法正确的有( )A.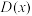 的定义域为R 的定义域为R | B.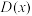 是非奇非偶函数 是非奇非偶函数 |
C.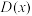 在实数集的任何区间上都不具有单调性 在实数集的任何区间上都不具有单调性 | D.任意非零有理数均是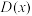 的周期 的周期 |
您最近一年使用:0次
解题方法
5 . 定义函数 为“正余弦”函数.结合学过的相关知识,我们可以得到该函数的性质:
为“正余弦”函数.结合学过的相关知识,我们可以得到该函数的性质:
1.我们知道,正弦函数 和余弦函数
和余弦函数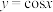 的定义域均为
的定义域均为 ,故函数
,故函数 的定义域为
的定义域为 .
.
2.我们知道,正弦函数 为奇函数,余弦函数
为奇函数,余弦函数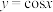 为偶函数,对
为偶函数,对 ,
,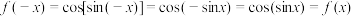 ,可得:函数
,可得:函数 为偶函数.
为偶函数.
3.我们知道,正弦函数 和余弦函数
和余弦函数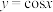 的最小正周期均为
的最小正周期均为 ,对
,对 ,
,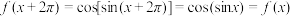 ,可知
,可知 为该函数的周期,是否是最小正周期呢?我们继续探究:
为该函数的周期,是否是最小正周期呢?我们继续探究: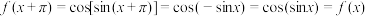 .可得:
.可得: 也为函数
也为函数 的周期.但是否为该函数的最小正周期呢?我们来研究
的周期.但是否为该函数的最小正周期呢?我们来研究 在区间
在区间 上的单调性,在区间
上的单调性,在区间 上,余弦函数
上,余弦函数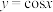 单调递减,正弦函数
单调递减,正弦函数 在
在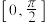 上单调递增,在
上单调递增,在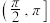 上单调递减,故我们需要分这两个区间来讨论.当
上单调递减,故我们需要分这两个区间来讨论.当 时,设
时,设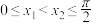 ,因正弦函数
,因正弦函数 在
在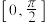 上单调递增,故
上单调递增,故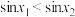 ,令
,令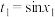 ,
,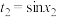 ,可得
,可得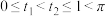 ,而在区间
,而在区间 上,余弦函数
上,余弦函数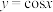 单调递减,故:
单调递减,故: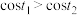 即:
即: 从而,
从而, 时,函数
时,函数 单调递减.同理可证,
单调递减.同理可证,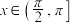 时,函数
时,函数 单调递增.可得,函数
单调递增.可得,函数 在
在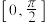 上单调递减,在
上单调递减,在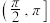 上单调递增.结合
上单调递增.结合 .可以确定:
.可以确定: 的最小正周期为
的最小正周期为 .这样,我们可以求出该函数的值域了:显然:
.这样,我们可以求出该函数的值域了:显然: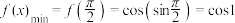 ,而
,而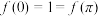 ,故
,故 的值域为
的值域为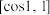 ,定义函数
,定义函数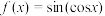 为“余正弦”函数,根据阅读材料的内容,解决下列问题:
为“余正弦”函数,根据阅读材料的内容,解决下列问题:
(1)求该函数的定义域;
(2)判断该函数的奇偶性;
(3)探究该函数的单调性及最小正周期,并求其值域.
 为“正余弦”函数.结合学过的相关知识,我们可以得到该函数的性质:
为“正余弦”函数.结合学过的相关知识,我们可以得到该函数的性质:1.我们知道,正弦函数
 和余弦函数
和余弦函数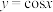 的定义域均为
的定义域均为 ,故函数
,故函数 的定义域为
的定义域为 .
.2.我们知道,正弦函数
 为奇函数,余弦函数
为奇函数,余弦函数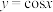 为偶函数,对
为偶函数,对 ,
,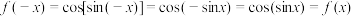 ,可得:函数
,可得:函数 为偶函数.
为偶函数.3.我们知道,正弦函数
 和余弦函数
和余弦函数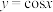 的最小正周期均为
的最小正周期均为 ,对
,对 ,
,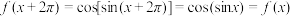 ,可知
,可知 为该函数的周期,是否是最小正周期呢?我们继续探究:
为该函数的周期,是否是最小正周期呢?我们继续探究: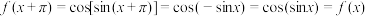 .可得:
.可得: 也为函数
也为函数 的周期.但是否为该函数的最小正周期呢?我们来研究
的周期.但是否为该函数的最小正周期呢?我们来研究 在区间
在区间 上的单调性,在区间
上的单调性,在区间 上,余弦函数
上,余弦函数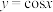 单调递减,正弦函数
单调递减,正弦函数 在
在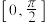 上单调递增,在
上单调递增,在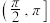 上单调递减,故我们需要分这两个区间来讨论.当
上单调递减,故我们需要分这两个区间来讨论.当 时,设
时,设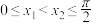 ,因正弦函数
,因正弦函数 在
在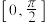 上单调递增,故
上单调递增,故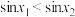 ,令
,令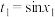 ,
,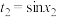 ,可得
,可得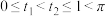 ,而在区间
,而在区间 上,余弦函数
上,余弦函数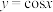 单调递减,故:
单调递减,故: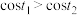 即:
即: 从而,
从而, 时,函数
时,函数 单调递减.同理可证,
单调递减.同理可证,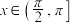 时,函数
时,函数 单调递增.可得,函数
单调递增.可得,函数 在
在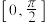 上单调递减,在
上单调递减,在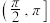 上单调递增.结合
上单调递增.结合 .可以确定:
.可以确定: 的最小正周期为
的最小正周期为 .这样,我们可以求出该函数的值域了:显然:
.这样,我们可以求出该函数的值域了:显然: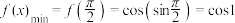 ,而
,而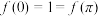 ,故
,故 的值域为
的值域为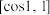 ,定义函数
,定义函数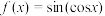 为“余正弦”函数,根据阅读材料的内容,解决下列问题:
为“余正弦”函数,根据阅读材料的内容,解决下列问题:(1)求该函数的定义域;
(2)判断该函数的奇偶性;
(3)探究该函数的单调性及最小正周期,并求其值域.
您最近一年使用:0次
解题方法
6 . 已知函数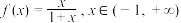 ,试判断函数
,试判断函数 的单调性,并证明.
的单调性,并证明.
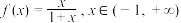 ,试判断函数
,试判断函数 的单调性,并证明.
的单调性,并证明.
您最近一年使用:0次
2020-05-22更新
|
1241次组卷
|
4卷引用:贵阳市普通高中2018-2019学年度高一上学期数学期末质量监测试题
贵阳市普通高中2018-2019学年度高一上学期数学期末质量监测试题贵州省贵阳市2018-2019学年高一(上)期末数学试题(已下线)专题03函数的单调性和最值-解题模板(已下线)专题03函数的单调性和最值解题模板A



