名校
解题方法
1 . 已知 ,
,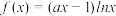 .
.
(1)若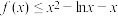 在
在 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(2)若 有两个极值点
有两个极值点 ,
, ,求a的范围并证明
,求a的范围并证明 .
.
 ,
,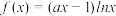 .
.(1)若
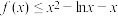 在
在 恒成立,求
恒成立,求 的取值范围;
的取值范围;(2)若
 有两个极值点
有两个极值点 ,
, ,求a的范围并证明
,求a的范围并证明 .
.
您最近一年使用:0次
2018-03-21更新
|
719次组卷
|
4卷引用:四川省成都市石室中学高2018届高三下期二诊模拟考试数学文试卷
2 . 已知函数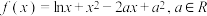 .
.
(1)若 ,求函数
,求函数 在
在 上的最小值;
上的最小值;
(2)若函数 在
在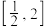 上存在单调递增区间,求实数
上存在单调递增区间,求实数 的取值范围;
的取值范围;
(3)根据 的不同取值,讨论函数
的不同取值,讨论函数 的极值点情况.
的极值点情况.
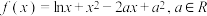 .
.(1)若
 ,求函数
,求函数 在
在 上的最小值;
上的最小值;(2)若函数
 在
在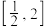 上存在单调递增区间,求实数
上存在单调递增区间,求实数 的取值范围;
的取值范围;(3)根据
 的不同取值,讨论函数
的不同取值,讨论函数 的极值点情况.
的极值点情况.
您最近一年使用:0次
2016-12-04更新
|
1420次组卷
|
2卷引用:2016届天津市和平区高三第四次模拟理科数学试卷
名校
3 . 已知 为实数,函数
为实数,函数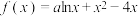 .
.
(1)若 是函数
是函数 的一个极值点,求实数
的一个极值点,求实数 的取值;
的取值;
(2)设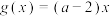 ,若
,若 ,使得
,使得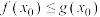 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 为实数,函数
为实数,函数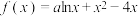 .
.(1)若
 是函数
是函数 的一个极值点,求实数
的一个极值点,求实数 的取值;
的取值;(2)设
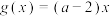 ,若
,若 ,使得
,使得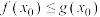 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2017-09-23更新
|
1448次组卷
|
8卷引用:广西桂林市柳州市2018年届高三综合模拟金卷(1)理科数学试题
广西桂林市柳州市2018年届高三综合模拟金卷(1)理科数学试题广西桂林市柳州市2018年届高三综合模拟金卷(1)文科数学试题山东省栖霞市第一中学2018届高三4月模拟考试数学(理)试题黑龙江省牡丹江市第一高级中学2018-2019学年高二下学期期末数学(文)试题四川省宜宾市叙州区第一中学校2019-2020学年高二下学期第四学月考试数学(文)试题陕西省榆林市定边县第四中学2023届高三上学期第二次月考理科数学试题安徽省合肥市庐江县五校2022-2023学年高三上学期期末联考数学试题(已下线)第七章 导数与不等式能成立(有解)问题 专题一 单变量不等式能成立(有解)之参变分离法 微点1 单变量不等式能成立(有解)之参变分离法
解题方法
4 . 已知函数 ,
, ,其中
,其中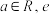 为自然对数的底数.
为自然对数的底数.
(1)求不等式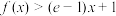 的解集;
的解集;
(2)若函数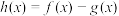 有两个极值点
有两个极值点 ,
, (
( )(若
)(若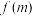 是函数
是函数 的极大值或极小值,则m为函数
的极大值或极小值,则m为函数 的极值点,极大值点与极小值点统称为极值点).
的极值点,极大值点与极小值点统称为极值点).
①求a的取值范围;
②证明: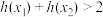 .
.
 ,
, ,其中
,其中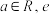 为自然对数的底数.
为自然对数的底数.(1)求不等式
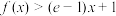 的解集;
的解集;(2)若函数
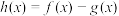 有两个极值点
有两个极值点 ,
, (
( )(若
)(若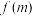 是函数
是函数 的极大值或极小值,则m为函数
的极大值或极小值,则m为函数 的极值点,极大值点与极小值点统称为极值点).
的极值点,极大值点与极小值点统称为极值点).①求a的取值范围;
②证明:
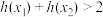 .
.
您最近一年使用:0次
名校
5 . 已知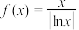 .
.
(1)求 的单调区间;
的单调区间;
(2)若方程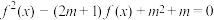 有4个不同实数根,求
有4个不同实数根,求 的取值范围;
的取值范围;
(3)若存在正实数 且
且 ,使得不等式
,使得不等式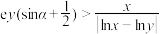 成立,求
成立,求 的解集.(其中
的解集.(其中 是自然对数的底数)
是自然对数的底数)
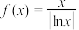 .
.(1)求
 的单调区间;
的单调区间;(2)若方程
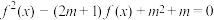 有4个不同实数根,求
有4个不同实数根,求 的取值范围;
的取值范围;(3)若存在正实数
 且
且 ,使得不等式
,使得不等式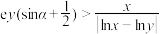 成立,求
成立,求 的解集.(其中
的解集.(其中 是自然对数的底数)
是自然对数的底数)
您最近一年使用:0次
6 . 已知函数 .
.
(1)求 的极值;
的极值;
(2)若关于 的不等式
的不等式 在
在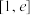 上的解集非空,求实数
上的解集非空,求实数 的取值范围.
的取值范围.
 .
.(1)求
 的极值;
的极值;(2)若关于
 的不等式
的不等式 在
在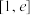 上的解集非空,求实数
上的解集非空,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
7 . 函数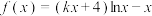 (
( ),若
),若 的解集为
的解集为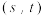 ,且
,且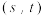 中只有一个整数,则实数
中只有一个整数,则实数 的取值范围为
的取值范围为
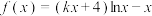 (
( ),若
),若 的解集为
的解集为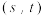 ,且
,且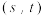 中只有一个整数,则实数
中只有一个整数,则实数 的取值范围为
的取值范围为A.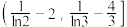 | B.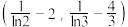 |
C.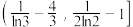 | D. |
您最近一年使用:0次
2018-08-06更新
|
770次组卷
|
5卷引用:2017届山东潍坊市高三理上学期期中联考数学试卷



