名校
解题方法
1 . 已知定义在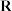 上的函数
上的函数 满足
满足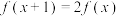 ,当
,当 时,
时,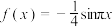 ,若对任意
,若对任意 ,都有
,都有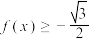 ,则
,则 的取值范围是( )
的取值范围是( )
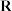 上的函数
上的函数 满足
满足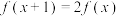 ,当
,当 时,
时, ,若对任意
,若对任意 ,都有
,都有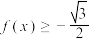 ,则
,则 的取值范围是( )
的取值范围是( )A.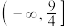 | B.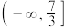 | C.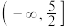 | D.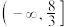 |
您最近一年使用:0次
2024-09-01更新
|
366次组卷
|
12卷引用:江苏省无锡市辅仁高级中学2025届高三上学期10月联合调研数学试卷
江苏省无锡市辅仁高级中学2025届高三上学期10月联合调研数学试卷四川省巴中市2022-2023学年高三上学期零诊考试数学(理科)试题湖南省邵阳市邵东市第一中学2022-2023学年高三上学期第二次月考数学试题四川省成都市简阳市阳安中学2022-2023学年高三上学期10月月考数学(理科)试题河北省邯郸市魏县2022-2023学年高一上学期期末考试数学试题河北省石家庄市行唐启明中学2022-2023学年高二下学期开学考试数学试题辽宁省铁岭市清河高级中学2022-2023学年高一下学期3月月考数学试题上海市交通大学附属中学2022-2023学年高一下学期3月卓越考试数学试题(已下线)模块二 大招13 类周期函数(已下线)第五章 三角函数(单元测试卷)-【同步题型讲义】(人教A版2019必修第一册)河北省邢台市南宫中学2024届高三下学期高考模拟数学试题湖南省邵东市创新高级中学2025届高三上学期第一次月考数学试题
名校
解题方法
2 . 下列结论正确的是( )
A.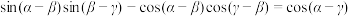 |
B.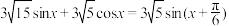 |
C.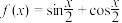 的最大值为 的最大值为 |
D.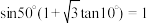 |
您最近一年使用:0次
名校
3 . 已知函数 .
.
(1)已知 ,且函数
,且函数 的最小正周期为
的最小正周期为 ,求函数
,求函数 图象的对称中心及其单调减区间;
图象的对称中心及其单调减区间;
(2)若 ,函数
,函数 在
在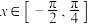 上的最值及其对应的
上的最值及其对应的 的值.
的值.
 .
.(1)已知
 ,且函数
,且函数 的最小正周期为
的最小正周期为 ,求函数
,求函数 图象的对称中心及其单调减区间;
图象的对称中心及其单调减区间;(2)若
 ,函数
,函数 在
在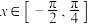 上的最值及其对应的
上的最值及其对应的 的值.
的值.
您最近一年使用:0次
2024-01-08更新
|
1277次组卷
|
4卷引用:江苏省无锡市天一中学2023-2024学年高一上学期12月阶段测试数学试卷
江苏省无锡市天一中学2023-2024学年高一上学期12月阶段测试数学试卷(已下线)专题05 三角函数1-2024年高一数学寒假作业单元合订本内蒙古赤峰市林西县第一中学2023-2024学年高一上学期期末测试数学试题(B)(已下线)高一数学开学摸底考02-江苏专用开学摸底考试卷
名校
解题方法
4 . 已知集合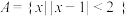 ,
, ,则
,则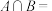 ( ).
( ).
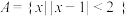 ,
, ,则
,则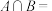 ( ).
( ).A.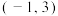 | B.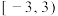 | C. | D.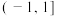 |
您最近一年使用:0次
2023-04-16更新
|
825次组卷
|
4卷引用:江苏省江阴市成化高级中学2023-2024学年高三上学期开学调研考试数学试题
名校
解题方法
5 . 如图所示,在平面四边形 中,
中,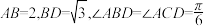 ,设
,设 .
.
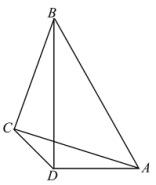
(1)若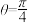 ,求
,求 的长;
的长;
(2)当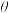 为何值时,△
为何值时,△ 的面积取得最大值,并求出该最大值.
的面积取得最大值,并求出该最大值.
 中,
中,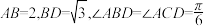 ,设
,设 .
.
(1)若
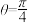 ,求
,求 的长;
的长;(2)当
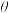 为何值时,△
为何值时,△ 的面积取得最大值,并求出该最大值.
的面积取得最大值,并求出该最大值.
您最近一年使用:0次
2022-10-18更新
|
2250次组卷
|
11卷引用:江苏省无锡市第一中学2022-2023学年高三上学期10月月考数学试题
江苏省无锡市第一中学2022-2023学年高三上学期10月月考数学试题江苏省无锡市市北高级中学2023-2024学年高三上学期10月阶段检测数学试题山东省威海市2022届高三下学期三模数学试题福建省厦门市集美中学2023届高三上学期10月月考数学试题(已下线)2023届高三第三次月考押题卷(测试范围:集合至立体几何)(已下线)模拟卷01山东省济南市莱芜第一中学2022-2023学年高三上学期12月月考数学试题河北省唐山市第一中学2022-2023学年高三上学期12月月考数学试题福建省连江第一中学2023届高三上学期期中数学试题福建省莆田哲理中学2024届高三上学期期中考试数学试题安徽省安庆市田家炳中学(安庆市第十中学)2024届高三上学期12月月考数学试卷
名校
解题方法
6 . 已知函数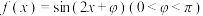 的图象关于点
的图象关于点 对称.
对称.
(1)求 的值;
的值;
(2)将函数 的图象向右平移
的图象向右平移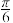 个单位,然后将所得的图象上各点的横坐标缩小到原来的
个单位,然后将所得的图象上各点的横坐标缩小到原来的 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 的图象.当
的图象.当 时,求函数
时,求函数 的值域.
的值域.
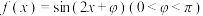 的图象关于点
的图象关于点 对称.
对称.(1)求
 的值;
的值;(2)将函数
 的图象向右平移
的图象向右平移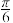 个单位,然后将所得的图象上各点的横坐标缩小到原来的
个单位,然后将所得的图象上各点的横坐标缩小到原来的 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 的图象.当
的图象.当 时,求函数
时,求函数 的值域.
的值域.
您最近一年使用:0次
2022-02-20更新
|
1219次组卷
|
3卷引用:江苏省无锡市天一中学2021-2022学年高一平行班上学期期末数学试题
7 . 已知点 在圆
在圆 上,点
上,点 的坐标为
的坐标为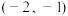 ,
, 为坐标原点,则
为坐标原点,则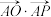 的最小值等于( )
的最小值等于( )
 在圆
在圆 上,点
上,点 的坐标为
的坐标为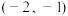 ,
, 为坐标原点,则
为坐标原点,则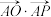 的最小值等于( )
的最小值等于( )A. | B. | C. | D.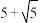 |
您最近一年使用:0次
8 . 已知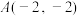 ,
,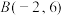 ,
,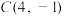 三点,点
三点,点 在圆
在圆 上运动,则
上运动,则 的最大值为
的最大值为________ ;最小值为________ .
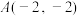 ,
,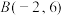 ,
,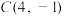 三点,点
三点,点 在圆
在圆 上运动,则
上运动,则 的最大值为
的最大值为
您最近一年使用:0次
名校
9 . 已知函数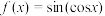 ,下列关于该函数结论正确的是( )
,下列关于该函数结论正确的是( )
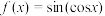 ,下列关于该函数结论正确的是( )
,下列关于该函数结论正确的是( )A. 的一个周期是 的一个周期是 |
B. 的图象关于直线 的图象关于直线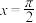 对称 对称 |
C. 的最大值小于 的最大值小于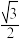 |
D.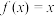 在区间( 在区间(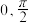 )内有唯一的根 )内有唯一的根 |
您最近一年使用:0次
2021-04-14更新
|
517次组卷
|
3卷引用:江苏省无锡市江阴市2021-2022学年高三上学期开学学情检测数学试题
名校
解题方法
10 . 已知函数 (
( ,
, ,
, )的一段图象如图所示.
)的一段图象如图所示.

(1)求函数 的单调递增区间;
的单调递增区间;
(2)若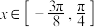 ,求函数
,求函数 的值域.
的值域.
 (
( ,
, ,
, )的一段图象如图所示.
)的一段图象如图所示.
(1)求函数
 的单调递增区间;
的单调递增区间;(2)若
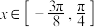 ,求函数
,求函数 的值域.
的值域.
您最近一年使用:0次
2020-09-14更新
|
907次组卷
|
7卷引用:江苏省无锡市梅村高中2017~2018学年高二第二学期数学(文)月考试卷



