1 . 在等差数列 中,
中,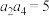 ,且
,且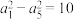 ,则
,则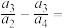
______ .
 中,
中,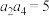 ,且
,且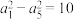 ,则
,则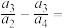
您最近一年使用:0次
解题方法
2 . 已知等差数列 的首项
的首项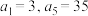 ,若在
,若在 中每相邻两项间插入1项,使其与原数列的数构成新的等差数列
中每相邻两项间插入1项,使其与原数列的数构成新的等差数列 ,则数列
,则数列 的通项公式为
的通项公式为______ .
 的首项
的首项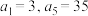 ,若在
,若在 中每相邻两项间插入1项,使其与原数列的数构成新的等差数列
中每相邻两项间插入1项,使其与原数列的数构成新的等差数列 ,则数列
,则数列 的通项公式为
的通项公式为
您最近一年使用:0次
解题方法
3 . 已知数列 中,
中,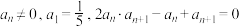 ,则
,则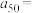 ( )
( )
 中,
中,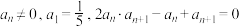 ,则
,则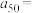 ( )
( )A. | B. | C.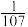 | D. |
您最近一年使用:0次
名校
4 . 某公司购置了一台价值220万元的设备,随着设备在使用过程中老化,其价值会逐年减少.经验表明,每经过一年其价值就会减少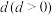 万元.已知这台设备的使用年限为10年,超过10年,它的价值将低于购进价值的
万元.已知这台设备的使用年限为10年,超过10年,它的价值将低于购进价值的 ,设备将报废,但若每年花费1万元进行设备维护,则可使设备的使用年限提升至20年,每经过一年其价值就会减少
,设备将报废,但若每年花费1万元进行设备维护,则可使设备的使用年限提升至20年,每经过一年其价值就会减少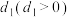 万元,超过20年,它的价值将低于所有花费的
万元,超过20年,它的价值将低于所有花费的 ,设备将报废,则
,设备将报废,则 的取值范围为
的取值范围为______ .
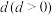 万元.已知这台设备的使用年限为10年,超过10年,它的价值将低于购进价值的
万元.已知这台设备的使用年限为10年,超过10年,它的价值将低于购进价值的 ,设备将报废,但若每年花费1万元进行设备维护,则可使设备的使用年限提升至20年,每经过一年其价值就会减少
,设备将报废,但若每年花费1万元进行设备维护,则可使设备的使用年限提升至20年,每经过一年其价值就会减少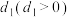 万元,超过20年,它的价值将低于所有花费的
万元,超过20年,它的价值将低于所有花费的 ,设备将报废,则
,设备将报废,则 的取值范围为
的取值范围为
您最近一年使用:0次
2024-09-27更新
|
154次组卷
|
2卷引用:4.2.2 等差数列的性质和应用 课后作业-人教A版(2019)选择性必修第二册第四章 数列
名校
解题方法
5 . 已知数列 满足
满足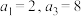 ,且
,且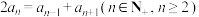 .
.
(1)求数列 的通项公式;
的通项公式;
(2)对于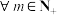 ,将数列
,将数列 中落在区间
中落在区间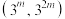 内的项的个数记为
内的项的个数记为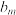 ,求数列
,求数列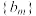 的通项公式.
的通项公式.
 满足
满足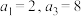 ,且
,且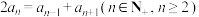 .
.(1)求数列
 的通项公式;
的通项公式;(2)对于
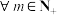 ,将数列
,将数列 中落在区间
中落在区间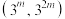 内的项的个数记为
内的项的个数记为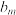 ,求数列
,求数列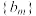 的通项公式.
的通项公式.
您最近一年使用:0次
2024-09-04更新
|
339次组卷
|
2卷引用:【课后练】 1.2.1等差数列及其通项公式+1.2.2 等差数列与一次函数 课后作业-湘教版(2019)选择性必修第一册 第1章 数列
6 . 在数列 中,
中, ,
, ,则
,则 等于( )
等于( )
 中,
中, ,
, ,则
,则 等于( )
等于( )A.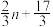 | B.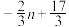 | C.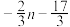 | D. |
您最近一年使用:0次
名校
解题方法
7 . 已知数列 满足
满足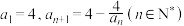 .
.
(1)求证: 是等差数列.
是等差数列.
(2)求数列 的通项公式.
的通项公式.
 满足
满足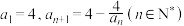 .
.(1)求证:
 是等差数列.
是等差数列.(2)求数列
 的通项公式.
的通项公式.
您最近一年使用:0次
2024-01-09更新
|
1142次组卷
|
5卷引用:5.2.1等差数列(分层练习,9大题型)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第三册)
(已下线)5.2.1等差数列(分层练习,9大题型)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第三册)(已下线)1.2.1 等差数列的概念及其通项公式(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)安徽省合肥市第一中学2023-2024学年高二上学期1月考数学考试试题(已下线)1.2.1 等差数列的概念及其通项公式8种常见考法归类(3)(已下线)专题06 等差数列与等比数列常考题型归类--高二期末考点大串讲(人教B版2019选择性必修第三册)
名校
解题方法
8 . 已知在等差数列 中,
中,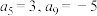 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 的前
的前 项和
项和 ,则当
,则当 为何值时
为何值时 取得最大,并求出此最大值.
取得最大,并求出此最大值.
 中,
中,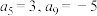 .
.(1)求数列
 的通项公式;
的通项公式;(2)若数列
 的前
的前 项和
项和 ,则当
,则当 为何值时
为何值时 取得最大,并求出此最大值.
取得最大,并求出此最大值.
您最近一年使用:0次
2024-01-09更新
|
4435次组卷
|
15卷引用:1.2.2等差数列的前n项和公式(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)
(已下线)1.2.2等差数列的前n项和公式(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)江苏省宿迁市青华中学2023-2024学年高二上学期期中考试普通班数学试卷(已下线)5.2.2 等差数列的前n项和(3知识点+8题型+强化训练)-【帮课堂】2023-2024学年高二数学同步学与练(人教B版2019选择性必修第三册)(已下线)第五章:数列(单元测试)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第三册)(已下线)重难点02:求数列前n项和常用10种解题策略-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)宁夏银川市贺兰县第一中学2023-2024学年高二下学期第一阶段考试数学试卷北京市第九中学2023-2024学年高二下学期4月月考数学试卷(已下线)模块一专题1《数列基础、等差数列和等比数列》单元检测篇A基础卷(高二人教B版)(已下线)模块一 专题2《数列基础、等差数列和等比数列》单元检测篇A基础卷(高二北师大版)四川省内江市第一中学2023-2024学年高二下学期第一次月考数学试题贵州省贵阳市清镇市博雅实验学校2023-2024学年高二下学期第三次月考数学试题宁夏石嘴山市平罗中学2023-2024学年高二上学期期末数学试题江西省宜春市万载第二中学2023-2024学年高二下学期第二次月考数学试卷西藏林芝市第二高级中学2023-2024学年高二下学期期中考试数学试题江西省赣州立德虔州高级中学2024届高三下学期第一次月考数学试卷
名校
解题方法
9 . 已知 是等差数列
是等差数列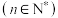 ,若
,若 ,
, .
.
(1)求 的通项公式;
的通项公式;
(2)证明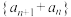 是等差数列.
是等差数列.
 是等差数列
是等差数列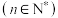 ,若
,若 ,
, .
.(1)求
 的通项公式;
的通项公式;(2)证明
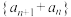 是等差数列.
是等差数列.
您最近一年使用:0次
2023-12-12更新
|
1110次组卷
|
7卷引用:1.2.1 等差数列的概念及其通项公式(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)
(已下线)1.2.1 等差数列的概念及其通项公式(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)【课后练】 1.2.1等差数列及其通项公式+1.2.2 等差数列与一次函数 课后作业-湘教版(2019)选择性必修第一册 第1章 数列河南省郑州市钱学森实验学校2023-2024学年高二上学期第二次月考数学试题(已下线)5.2.1 等差数列(4知识点+8题型+强化训练)-【帮课堂】2023-2024学年高二数学同步学与练(人教B版2019选择性必修第三册)(已下线)1.2.1 等差数列的概念及其通项公式8种常见考法归类(2)重庆市育才中学、西南大学附中、万州中学2023~2024学年高二上学期12月联考数学试题(已下线)4.2.1&4.2.2 等差数列的概念与等差数列的通项公式(8大题型)-【题型分类归纳】2023-2024学年高二数学同步讲与练(苏教版2019选择性必修第一册)
23-24高二·全国·假期作业
名校
10 . 等差数列 的公差
的公差 ,且
,且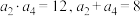 ,则数列
,则数列 的通项公式是( )
的通项公式是( )
 的公差
的公差 ,且
,且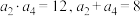 ,则数列
,则数列 的通项公式是( )
的通项公式是( )A.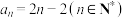 | B.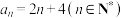 |
C.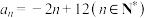 | D.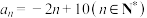 |
您最近一年使用:0次
2023-11-24更新
|
961次组卷
|
4卷引用:5.2.1等差数列(分层练习,9大题型)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第三册)
(已下线)5.2.1等差数列(分层练习,9大题型)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第三册)(已下线)1.2.1 等差数列的概念及其通项公式(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)(已下线)寒假作业(十二)等差数列经典题练湖北省襄阳市第五中学2023-2024学年高二上学期12月月考数学试卷



