解题方法
1 . 如图,在正四棱柱 中,
中, ,
, .
. 平面
平面 ;
;
(2)求点 到平面
到平面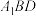 的距离.
的距离.
 中,
中, ,
, .
.
 平面
平面 ;
;(2)求点
 到平面
到平面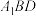 的距离.
的距离.
您最近一年使用:0次
解题方法
2 . 如图,在四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, 为
为 中点,PO⊥平面
中点,PO⊥平面 ,
, ,
, 为
为 中点.
中点.
 平面
平面 ;
;
(2)求四棱锥 的体积.
的体积.
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, 为
为 中点,PO⊥平面
中点,PO⊥平面 ,
, ,
, 为
为 中点.
中点.

 平面
平面 ;
;(2)求四棱锥
 的体积.
的体积.
您最近一年使用:0次
名校
解题方法
3 . 已知正方体 的棱长为1,P为AC的中点.
的棱长为1,P为AC的中点. 内找一点
内找一点 ,使
,使 //平面
//平面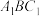 ,并证明;
,并证明;
(2)求三棱锥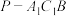 的体积和表面积.
的体积和表面积.
 的棱长为1,P为AC的中点.
的棱长为1,P为AC的中点.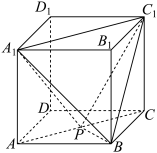
 内找一点
内找一点 ,使
,使 //平面
//平面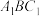 ,并证明;
,并证明;(2)求三棱锥
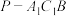 的体积和表面积.
的体积和表面积.
您最近一年使用:0次
解题方法
4 . 如图,已知正方体 的体积为8.
的体积为8. 的表面积;
的表面积;
(2)设上底面 的中心为
的中心为 ,求三棱锥
,求三棱锥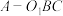 的体积;
的体积;
(3)求三棱锥 内切球(与所有面均相切的球)的半径.
内切球(与所有面均相切的球)的半径.
 的体积为8.
的体积为8.
 的表面积;
的表面积;(2)设上底面
 的中心为
的中心为 ,求三棱锥
,求三棱锥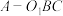 的体积;
的体积;(3)求三棱锥
 内切球(与所有面均相切的球)的半径.
内切球(与所有面均相切的球)的半径.
您最近一年使用:0次
2024-04-29更新
|
544次组卷
|
2卷引用:天津市重点校2023-2024学年高一下学期4月期中联考数学试题
2024·四川成都·模拟预测
名校
解题方法
5 . 在四棱锥 中,已知
中,已知

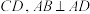 ,
, 是线段
是线段 上的点.
上的点. 底面
底面 ;
;
(2)是否存在点 使得三棱锥
使得三棱锥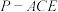 的体积为
的体积为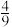 ?若存在,求出
?若存在,求出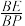 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 中,已知
中,已知

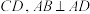 ,
, 是线段
是线段 上的点.
上的点.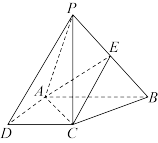
 底面
底面 ;
;(2)是否存在点
 使得三棱锥
使得三棱锥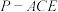 的体积为
的体积为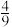 ?若存在,求出
?若存在,求出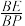 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2024-03-06更新
|
693次组卷
|
4卷引用:天津市第二耀华中学2023-2024学年高一下学期期中考试数学试卷
天津市第二耀华中学2023-2024学年高一下学期期中考试数学试卷(已下线)四川省成都市第七中学2024届高三下学期二诊模拟考试文科数学试卷(已下线)第3讲:立体几何中的探究问题【练】安徽省2024届新高考预测数学模拟卷(二)
解题方法
6 . 如图,四棱锥 的底面是菱形,平面
的底面是菱形,平面 底面
底面 ,
, ,
, 分别是
分别是 ,
, 的中点,
的中点, ,
,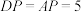 ,
, .
.
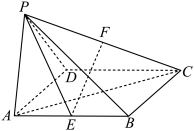
(1)求证: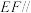 平面
平面 ;
;
(2)求证: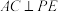 ;
;
(3)求四棱锥 的体积.
的体积.
 的底面是菱形,平面
的底面是菱形,平面 底面
底面 ,
, ,
, 分别是
分别是 ,
, 的中点,
的中点, ,
,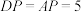 ,
, .
.
(1)求证:
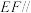 平面
平面 ;
;(2)求证:
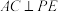 ;
;(3)求四棱锥
 的体积.
的体积.
您最近一年使用:0次
7 . 如图:在正方体 中
中 ,
, 为
为 的中点.
的中点.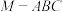 的体积;
的体积;
(2)求证: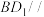 平面
平面 ;
;
(3)若 为
为 的中点,求证:平面
的中点,求证:平面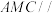 平面
平面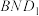 .
.
 中
中 ,
, 为
为 的中点.
的中点.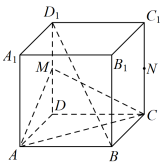
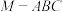 的体积;
的体积;(2)求证:
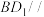 平面
平面 ;
;(3)若
 为
为 的中点,求证:平面
的中点,求证:平面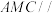 平面
平面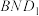 .
.
您最近一年使用:0次
2023-05-02更新
|
10353次组卷
|
19卷引用:天津市五所重点学校2022-2023学年高一下学期期中联考数学试题
天津市五所重点学校2022-2023学年高一下学期期中联考数学试题天津市第四十七中学2023-2024学年高一下学期5月期中考试数学试题天津市南仓中学2023-2024学年高一下学期4月期中检测数学试题重庆市荣昌中学校2023-2024学年高一下学期4月期中考试数学试题广东省深圳市南头中学2023-2024学年高一下学期期中考试数学试卷(已下线)专题训练:线线、线面、面面平行证明(已下线)第06讲 立体几何位置关系及距离专题期末高频考点题型秒杀山东省聊城市聊城第四中学2022-2023学年高一下学期5月月考数学试题宁夏吴忠市吴忠中学2022-2023学年高一下学期数学期末考试练习试题(已下线)第07讲 立体几何大题(11个必刷考点)-《考点·题型·密卷》(已下线)模块三 专题8(立体几何初步)拔高能力练(北师大版)(已下线)模块三 专题7 大题分类练(立体几何初步)拔高能力练(人教A)(已下线)模块三 专题8大题分类练(立体几何初步)拔高能力练(苏教版)(已下线)模块五 专题1 全真基础模拟1(苏教版高一)江苏省徐州市邳州市明德实验学校2022-2023学年高一下学期第二次月考数学试题山东省烟台市爱华学校2022-2023学年高一下学期第二次月中质量检测数学试题安徽省亳州市第二完全中学2023-2024学年高一下学期第二次月考(5月)数学试题山东省聊城市第一中学2023-2024学年高一下学期第二次阶段测试数学试题福建省福清西山学校2023-2024学年高一下学期5月月考数学试题
名校
解题方法
8 . 如图,三棱锥 的底面
的底面 的侧面
的侧面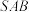 都是边长为2的等边三角形,
都是边长为2的等边三角形, ,
, 分别是
分别是 ,
, 的中点,
的中点, .
.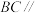 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
 的底面
的底面 的侧面
的侧面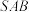 都是边长为2的等边三角形,
都是边长为2的等边三角形, ,
, 分别是
分别是 ,
, 的中点,
的中点, .
.
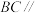 平面
平面 ;
;(2)求三棱锥
 的体积.
的体积.
您最近一年使用:0次
2023-04-24更新
|
1526次组卷
|
6卷引用:天津市部分区2022-2023学年高一下学期期中数学试题
天津市部分区2022-2023学年高一下学期期中数学试题内蒙古自治区通辽市科尔沁左翼中旗实验高级中学2022-2023学年高一下学期期中数学试题(已下线)立体几何专题:空间几何体体积的5种题型上海交通大学附属中学2024届高三上学期摸底数学试题(已下线)信息必刷卷01(文科专用)宁夏吴忠市2024届高三下学期高考模拟联考试卷(二)文科数学试题
2023高一·全国·专题练习
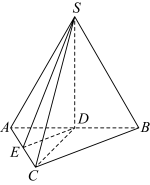
9 . 如图,已知正三棱锥S﹣ABC的底面边长为2,正三棱锥的高SO=1.
(2)求正三棱锥S﹣ABC表面积.

(2)求正三棱锥S﹣ABC表面积.
您最近一年使用:0次
2023-03-15更新
|
2300次组卷
|
13卷引用:天津市第三中学2022-2023学年高一下学期期中数学试题
天津市第三中学2022-2023学年高一下学期期中数学试题广东省江门市新会陈经纶中学2022-2023学年高一下学期期中数学试题(已下线)高一下学期期中模拟卷01(第六章至第八章8.3)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第二册)浙江省绍兴蕺山外国语学校2022-2023学年高一下学期期中数学试题(已下线)模块四 高一下期中重组篇(浙江)宁夏银川市2023-2024学年高一下学期期中考试数学试卷(已下线)8.3.1 棱柱、棱锥、棱台的表面积和体积(分层作业)-【上好课】2022-2023学年高一数学同步备课系列(人教A版2019必修第二册)(已下线)8.3.1 棱柱、棱锥、棱台的表面积和体积(1)-2022-2023学年高一数学《考点·题型·技巧》精讲与精练高分突破系列(人教A版2019必修第二册)(已下线)13.3 空间图形的表面积和体积(分层练习)(已下线)专题11 空间图形的表面积与体积-期中期末考点大串讲(苏教版2019必修第二册)(已下线)核心考点05简单几何体的表面积与体积(已下线)8.3.1棱柱、棱锥、棱台的表面积和体积(分层作业)-【上好课】福建省宁德市博雅培文学校2023-2024学年高一下学期第一次月考数学试题
名校
解题方法
10 . 鳖臑是我国古代对四个面均为直角三角形的三棱锥的称呼.如图,三棱锥 是一鳖臑,其中
是一鳖臑,其中 ,
,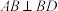 ,
, ,
,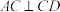 ,且高
,且高 ,
,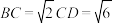 .
.
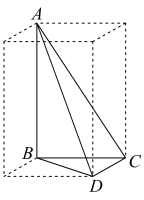
(1)求三棱锥 的体积和表面积;
的体积和表面积;
(2)求三棱锥 外接球体积和内切球的半径.
外接球体积和内切球的半径.
 是一鳖臑,其中
是一鳖臑,其中 ,
,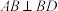 ,
, ,
,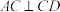 ,且高
,且高 ,
,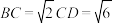 .
.
(1)求三棱锥
 的体积和表面积;
的体积和表面积;(2)求三棱锥
 外接球体积和内切球的半径.
外接球体积和内切球的半径.
您最近一年使用:0次
2022-04-24更新
|
1427次组卷
|
4卷引用:天津市第二十中学2022-2023学年高一下学期期中数学试题



