解题方法
1 . 某企业拟建造如图所示的容器(不计厚度,长度单位:m),其中容器的中间为圆柱体,左右两端均为半球体,按照设计要求容器的体积为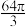 m3.假设该容器的建造费用仅与其表面积有关.已知圆柱体部分每平方米建造费用为3万元,半球体部分每平方米建造费用为4万元.设该容器的总建造费用为y万元.
m3.假设该容器的建造费用仅与其表面积有关.已知圆柱体部分每平方米建造费用为3万元,半球体部分每平方米建造费用为4万元.设该容器的总建造费用为y万元.
(2)确定r和l为何值时,该容器的建造费用最小,并求出最小建造费用.
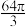 m3.假设该容器的建造费用仅与其表面积有关.已知圆柱体部分每平方米建造费用为3万元,半球体部分每平方米建造费用为4万元.设该容器的总建造费用为y万元.
m3.假设该容器的建造费用仅与其表面积有关.已知圆柱体部分每平方米建造费用为3万元,半球体部分每平方米建造费用为4万元.设该容器的总建造费用为y万元.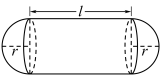
(2)确定r和l为何值时,该容器的建造费用最小,并求出最小建造费用.
您最近一年使用:0次
2023-12-18更新
|
467次组卷
|
4卷引用:人教A版(2019) 选修第二册 数学奇书 第五章 一元函数的导数及其应用 章末整合提升
人教A版(2019) 选修第二册 数学奇书 第五章 一元函数的导数及其应用 章末整合提升(已下线)第五章 一元函数的导数及其应用(单元综合测试卷)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)(已下线)专题05 导数的综合问题(九大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)山东省大联考2023-2024学年高二下学期3月月考数学试题
名校
2 . 已知圆锥的顶点为P,母线 所成角的余弦值为
所成角的余弦值为 ,轴截面等腰三角形的顶角为
,轴截面等腰三角形的顶角为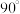 ,若
,若 的面积为
的面积为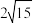 .
.
(1)求该圆锥的侧面积;
(2)求圆锥的内切球体积.
 所成角的余弦值为
所成角的余弦值为 ,轴截面等腰三角形的顶角为
,轴截面等腰三角形的顶角为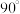 ,若
,若 的面积为
的面积为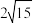 .
.(1)求该圆锥的侧面积;
(2)求圆锥的内切球体积.
您最近一年使用:0次
2023-11-13更新
|
467次组卷
|
5卷引用:考点7 组合体的内切 2024届高考数学考点总动员【练】
(已下线)考点7 组合体的内切 2024届高考数学考点总动员【练】江西省景德镇市昌江区景德镇一中2023-2024学年高二上学期11月期中考试数学试题(已下线)专题8.3 简单几何体的表面积与体积-举一反三系列(人教A版2019必修第二册)(已下线)高一下学期期中复习解答题压轴题十八大题型专练(2)-举一反三系列(人教A版2019必修第二册)山东省菏泽市菏泽一中系列2023-2024学年高一下学期4月期中考试数学试题(A)
解题方法
3 . 已知一个正方体的顶点都在球面上,它的棱长是4cm.求这个球的体积.
您最近一年使用:0次
2023-10-09更新
|
186次组卷
|
3卷引用:北师大版(2019)必修第二册课本习题 习题6-6
解题方法
4 . 球表面积膨胀为原来的2倍,体积变为原来的几倍?
您最近一年使用:0次
2023-10-09更新
|
99次组卷
|
3卷引用:北师大版(2019)必修第二册课本习题 习题6-6
5 . 设圆柱、圆锥的底面半径与球的半径都为r,圆柱、圆锥的高都是 .求它们的体积之比.
.求它们的体积之比.
 .求它们的体积之比.
.求它们的体积之比.
您最近一年使用:0次
2023-10-09更新
|
97次组卷
|
3卷引用:北师大版(2019)必修第二册课本习题 习题6-6
6 . 地球和火星都可近似看作球体,地球半径约为6370km,火星的直径约为地球的直径的一半.
(1)求地球的表面积和体积;
(2)火星的体积约为地球体积的几分之几?
(1)求地球的表面积和体积;
(2)火星的体积约为地球体积的几分之几?
您最近一年使用:0次
2023-10-09更新
|
176次组卷
|
4卷引用:北师大版(2019)必修第二册课本习题第六章6.3球的表面积和体积
北师大版(2019)必修第二册课本习题第六章6.3球的表面积和体积(已下线)6.3 球的表面积和体积北师大版(2019)必修第二册课本例题6.3 球的表面积和体积(已下线)专题13.6空间图形的表面积和体积-重难点突破及混淆易错规避(苏教版2019必修第二册)
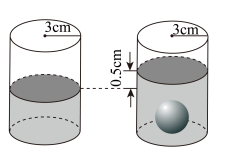
7 . 如图,一个装有水的圆柱形玻璃杯的内径为3cm.将一个玻璃球完全浸入水中,杯中水的高度上升了0.5cm.求玻璃球的半径.
您最近一年使用:0次
2023-10-05更新
|
204次组卷
|
2卷引用:湘教版(2019)必修第二册课本例题4.5.2 几种简单几何体的体积
名校
8 . 如图:三棱台 的六个顶点都在球
的六个顶点都在球 的球面上,球心位于上下底面所在的两个平行平面之间,
的球面上,球心位于上下底面所在的两个平行平面之间, ,
, 和
和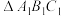 分别是边长为
分别是边长为 和
和 的正三角形.
的正三角形. 的表面积;
的表面积;
(2)计算球 的体积.
的体积.
 的六个顶点都在球
的六个顶点都在球 的球面上,球心位于上下底面所在的两个平行平面之间,
的球面上,球心位于上下底面所在的两个平行平面之间, ,
, 和
和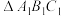 分别是边长为
分别是边长为 和
和 的正三角形.
的正三角形.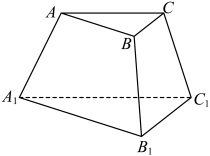
 的表面积;
的表面积;(2)计算球
 的体积.
的体积.
您最近一年使用:0次
2023-07-12更新
|
1078次组卷
|
10卷引用:山东省德州市2022-2023学年高一下学期期末数学试题
山东省德州市2022-2023学年高一下学期期末数学试题山东省德州市德城区第一中学2022-2023学年高一下学期期末数学试题(已下线)模块二 专题6 简单几何体的结构、表面积与体积 B巩固卷(人教B)(已下线)模块二 专题3 简单几何体的结构、表面积与体积 B提升卷(已下线)第07讲 空间几何体初步-【寒假预科讲义】(人教A版2019必修第一册)山东省青岛市第五十八中学2022-2023学年高一下学期5月阶段性模块考试数学试题(已下线)高一下学期期末复习解答题压轴题二十四大题型专练(2)-举一反三系列(人教A版2019必修第二册)(已下线)11.1.6 祖暅原理与几何体的体积-【帮课堂】(人教B版2019必修第四册)【人教A版(2019)】专题13立体几何与空间向量(第二部分)-高一下学期名校期末好题汇编(已下线)专题07 空间几何体-【暑假自学课】(人教B版2019必修第四册)
解题方法
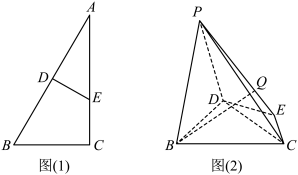
9 . 如图(1)所示,在 中,
中,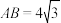 ,
, ,
, ,
, 垂直平分
垂直平分 .现将
.现将 沿
沿 折起,使得二面角
折起,使得二面角 大小为
大小为 ,得到如图(2)所示的空间几何体(折叠后点
,得到如图(2)所示的空间几何体(折叠后点 记作点
记作点 )
) 到面
到面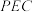 的距离;
的距离;
(2)求四棱锥 外接球的体积;
外接球的体积;
(3)点 为一动点,满足
为一动点,满足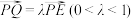 ,当直线
,当直线 与平面
与平面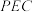 所成角最大时,试确定点
所成角最大时,试确定点 的位置.
的位置.
 中,
中,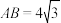 ,
, ,
, ,
, 垂直平分
垂直平分 .现将
.现将 沿
沿 折起,使得二面角
折起,使得二面角 大小为
大小为 ,得到如图(2)所示的空间几何体(折叠后点
,得到如图(2)所示的空间几何体(折叠后点 记作点
记作点 )
)
 到面
到面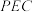 的距离;
的距离;(2)求四棱锥
 外接球的体积;
外接球的体积;(3)点
 为一动点,满足
为一动点,满足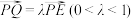 ,当直线
,当直线 与平面
与平面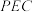 所成角最大时,试确定点
所成角最大时,试确定点 的位置.
的位置.
您最近一年使用:0次
2023-06-30更新
|
1129次组卷
|
11卷引用:江苏省宿迁市2022-2023学年高二下学期期末数学试题
江苏省宿迁市2022-2023学年高二下学期期末数学试题(已下线)专题1.6 空间角的向量求法大题专项训练(30道)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)专题4 立体几何与函数最值(已下线)考点12 空间角 2024届高考数学考点总动员 【讲】(已下线)专题1-3 空间向量综合:斜棱柱、不规则几何体建系计算(讲+练)-【巅峰课堂】2023-2024学年高二数学热点题型归纳与培优练(人教A版2019选择性必修第一册)(已下线)第02讲:空间向量与立体几何交汇(必刷6大考题+7大题型)-2023-2024学年高二数学上学期《考点·题型·难点》期末高效复习(人教A版2019选择性必修第一册)(已下线)通关练04 空间向量与立体几何大题9考点精练(41题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)(已下线)第02讲 空间向量的应用(2)(已下线)第二章 立体几何中的计算 专题六 几何体的外接球、棱切球、内切球 微点12 二面角的四面体模型综合训练【基础版】(已下线)第二章 立体几何中的计算 专题七 空间范围与最值问题 微点8 空间范围与最值问题综合训练【江苏专用】专题09立体几何与空间向量(第一部分)-高二下学期名校期末好题汇编
名校
10 . 在正四棱柱 中,
中,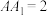 ,M是
,M是 的中点.
的中点.

(1)证明: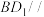 平面
平面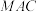 .
.
(2)若正四棱柱的表面积是10,求该正四棱柱的外接球的体积.
 中,
中,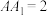 ,M是
,M是 的中点.
的中点.
(1)证明:
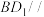 平面
平面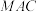 .
.(2)若正四棱柱的表面积是10,求该正四棱柱的外接球的体积.
您最近一年使用:0次



