名校
解题方法
1 . 如图1是一栋度假别墅,它的屋顶可近似看作一个多面体,图2是该屋顶的结构示意图,其中四边形 和四边形
和四边形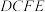 是两个全等的等腰梯形,
是两个全等的等腰梯形,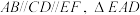 和
和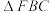 是两个全等的正三角形.已知该多面体的棱
是两个全等的正三角形.已知该多面体的棱 与平面
与平面 成的角
成的角 ,
, ,则该屋顶的侧面积为( )
,则该屋顶的侧面积为( )
 和四边形
和四边形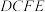 是两个全等的等腰梯形,
是两个全等的等腰梯形,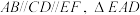 和
和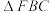 是两个全等的正三角形.已知该多面体的棱
是两个全等的正三角形.已知该多面体的棱 与平面
与平面 成的角
成的角 ,
, ,则该屋顶的侧面积为( )
,则该屋顶的侧面积为( )
| A.80 | B.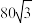 | C.160 | D.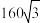 |
您最近一年使用:0次
2023-12-16更新
|
416次组卷
|
3卷引用:江苏省徐州市2024届高三上学期合格考试学情调研数学试题
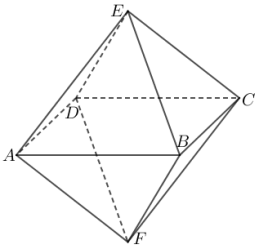
2 . 正多面体被古希腊圣哲认为是构成宇宙的基本元素,加上它们的多种变体,一直是科学、艺术、哲学灵感的源泉之一.如图,该几何体是一个棱长为2的正八面体,则此正八面体的体积与表面积之比为___________ .

您最近一年使用:0次
2022-01-10更新
|
792次组卷
|
4卷引用:第24讲 棱柱、棱锥、棱台的表面积和体积 2
解题方法
3 . 陀螺起源于我国,在山西夏县新石器时代的遗址中,就出土了目前发现的最早的石制陀螺因此,陀螺的历史至少也有四千年,如图所示为一个陀螺的立体结构图,若该陀螺底面圆的直径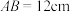 ,圆柱体部分的高
,圆柱体部分的高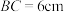 ,圆锥体部分的高
,圆锥体部分的高 ,则这个陀螺的表面积是( )
,则这个陀螺的表面积是( )
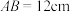 ,圆柱体部分的高
,圆柱体部分的高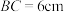 ,圆锥体部分的高
,圆锥体部分的高 ,则这个陀螺的表面积是( )
,则这个陀螺的表面积是( )
A.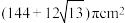 | B.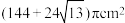 |
C.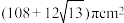 | D.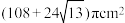 |
您最近一年使用:0次
4 . 如图截角四面体是一种半正八面体,可由四面体经过适当的截角,即截去四面体的四个顶点所产生的多面体.如图,将棱长为3的正四面体沿棱的三等分点作平行于底面的截面得到所有棱长均为1的截角四面体.
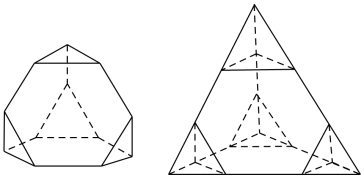
(1)该截角四面体的表面积;
(2)该截角四面体的体积.

(1)该截角四面体的表面积;
(2)该截角四面体的体积.
您最近一年使用:0次
2022-06-07更新
|
755次组卷
|
3卷引用:第22讲 复杂多面体的表面积与体积
解题方法
5 . 截角四面体是由四面体经过适当的截角,即截去四面体的四个顶点处的小棱锥所得的多面体.如图,将棱长为6的正四面体沿棱的三等分点作平行于底面的截面,得到所有棱长均为2的截角四面体,则( )
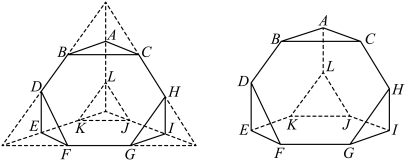

A.直线 与平面 与平面 所成角为 所成角为 |
B. |
C.该截角四面体的表面积为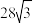 |
D.该截角四面体外接球的表面积为 |
您最近一年使用:0次
名校
解题方法
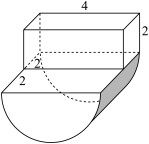
6 . 某几何体的直观图如图所示,则该几何体的表面积为( )
A. | B. |
C. | D.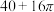 |
您最近一年使用:0次
2022-04-29更新
|
607次组卷
|
4卷引用:山西省大同市浑源县第七中学校2022-2023学年高一下学期期末考试数学试题
2023高三·全国·专题练习
解题方法
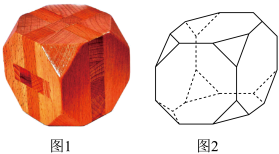
7 . 鲁班锁(也称孔明锁、难人木、六子联方)起源于古代中国建筑的榫卯结构.如图1,这是一种常见的鲁班锁玩具,图2是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁的表面积为( )
A.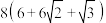 | B.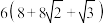 |
C. | D.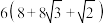 |
您最近一年使用:0次
2022-09-15更新
|
633次组卷
|
6卷引用:第49讲 空间几何体的表面积与体积
(已下线)第49讲 空间几何体的表面积与体积(已下线)第22讲 复杂多面体的表面积与体积2023版 湘教版(2019) 必修第二册 过关斩将 第4章 专题强化练9 数学文化背景下的空间几何体问题第 11 章 简单几何体 综合测试【3】(已下线)8.3简单几何体的表面积与体积——课后作业(提升版)(已下线)第二节 组合体问题【同步课时】提升卷
名校
解题方法
8 . 半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体体现了数学的对称美.如图是一个棱数为24的半正多面体,它的所有顶点都在同一个正方体的棱上,且此正方体的棱长为4,则该半正多面体的表面积为_____________ .
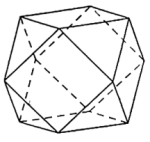

您最近一年使用:0次
名校
解题方法
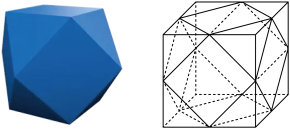
9 . “阿基米德多面体”也称为半正多面体,半正多面体是由两种或多种正多边形面组成,而又不属于正多面体的凸多面体.如图,某广场的一张石凳就是一个阿基米德多面体,它是由正方体截去八个一样的四面体得到的.若被截正方体的棱长为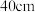 ,则该阿基米德多面体的表面积为( )
,则该阿基米德多面体的表面积为( )
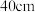 ,则该阿基米德多面体的表面积为( )
,则该阿基米德多面体的表面积为( )
A.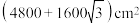 | B. |
C. | D. |
您最近一年使用:0次
2022-12-17更新
|
661次组卷
|
5卷引用:辽宁省沈阳市浑南区东北育才学校科学高中部2023-2024学年高三上学期高考适应性测试(一)数学试题
辽宁省沈阳市浑南区东北育才学校科学高中部2023-2024学年高三上学期高考适应性测试(一)数学试题吉林省四平市第一高级中学2021-2022学年高三上学期第四次月考数学(理)试题吉林省四平市第一高级中学2021-2022学年高三上学期第四次月考数学(文)试题内蒙古呼伦贝尔市额尔古纳市第一中学2021-2022学年高一上学期期末数学试题(已下线)第六章 突破立体几何创新问题 专题二 交汇世界文化 微点2 与世界文化遗产有关的的立体几何问题综合训练【基础版】
10 . “阿基米德多面体”也称为半正多面体(semi-regularsolid),是由边数不全相同的正多边形为面围成的多面体,它体现了数学的对称美.如图所示,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共可截去八个三棱锥,得到八个面为正三角形、六个面为正方形的一种半正多面体,已知 ,则关于如图半正多面体的下列说法中,正确的有( )
,则关于如图半正多面体的下列说法中,正确的有( )
 ,则关于如图半正多面体的下列说法中,正确的有( )
,则关于如图半正多面体的下列说法中,正确的有( )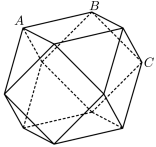
A.该半正多面体的体积为 |
B.该半正多面体过A,B,C三点的截面面积为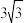 |
C.该半正多面体外接球的表面积为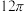 |
D.该半正多面体的顶点数V、面数F、棱数E满足关系式 |
您最近一年使用:0次
2022-05-04更新
|
633次组卷
|
5卷引用:专题21 空间几何体(针对训练)-2023年高考数学一轮复习精讲精练宝典(新高考专用)
(已下线)专题21 空间几何体(针对训练)-2023年高考数学一轮复习精讲精练宝典(新高考专用)(已下线)第22讲 复杂多面体的表面积与体积河北省邢台市卓越联盟2021-2022学年高一下学期第二次月考数学试题福建省德化第二中学2023-2024学年高一下学期期中考试数学试题山东省临沂市莒南县第一中学2023-2024学年高一下学期5月月考数学试题



