解题方法
1 . 如图,正方体 的棱长为3,点
的棱长为3,点 在棱
在棱 上,点
上,点 在棱
在棱 上,
上, 在棱
在棱 上,且
上,且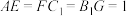 ,
, 是棱
是棱 上一点.
上一点. ,
, ,
, ,
, 四点共面;
四点共面;
(2)若平面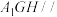 平面
平面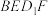 ,求证:
,求证: 为
为 的中点.
的中点.
(3)求平面 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.
 的棱长为3,点
的棱长为3,点 在棱
在棱 上,点
上,点 在棱
在棱 上,
上, 在棱
在棱 上,且
上,且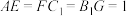 ,
, 是棱
是棱 上一点.
上一点.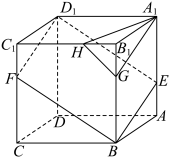
 ,
, ,
, ,
, 四点共面;
四点共面;(2)若平面
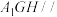 平面
平面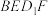 ,求证:
,求证: 为
为 的中点.
的中点.(3)求平面
 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.
您最近一年使用:0次
2024-06-17更新
|
195次组卷
|
2卷引用:海南省2020-2021学年高二下学期期末考试数学试题
名校
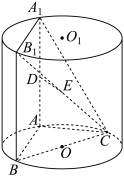
2 . 如图, ,
, 为圆柱
为圆柱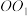 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, ,
, 分别是
分别是 ,
,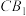 的中点,
的中点, 平面
平面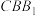 .
.
(1)证明:
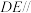 平面
平面 ;
;(2)若
 ,求平面
,求平面 与平面
与平面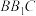 的夹角余弦值.
的夹角余弦值.
您最近一年使用:0次
2016高一·全国·课后作业
解题方法
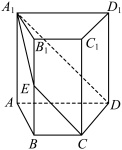
3 . 如图,在四棱柱 中,底面
中,底面 为梯形,
为梯形, ,平面
,平面 与
与 交于点
交于点 .求证:
.求证: .
.
 中,底面
中,底面 为梯形,
为梯形, ,平面
,平面 与
与 交于点
交于点 .求证:
.求证: .
.
您最近一年使用:0次
2023-06-13更新
|
1506次组卷
|
23卷引用:【新教材精创】13.2.4平面与平面的位置关系—两平面平行的判定与性质练习
(已下线)【新教材精创】13.2.4平面与平面的位置关系—两平面平行的判定与性质练习北师大版 必修2 过关斩将 第一章 立体几何初步 §5 平行关系 5.2 平行关系的性质(已下线)同步君人教A版必修2第二章2.2.4平面与平面平行的性质高中数学人教版 必修2 第二章 点、直线、平面之间的位置关系 2.2.4平面与平面平行的性质人教A版高中数学必修二2.2.4平面与平面平行的性质1人教A版(2019) 必修第二册 过关斩将 第八章 8.5. 空间直线、平面的平行 8.5.3 平面与平面平行人教B版(2019) 必修第四册 过关斩将 第十一章 立体几何初步 11.3.3 平面与平面平行人教A版(2019) 必修第二册 突围者(经验篇) 第8章 第4节空间点、直线、平面之间的位置关系+第5节空间直线、平面的平行(已下线)考点22 空间几何平行问题(练习)-2021年高考数学复习一轮复习笔记(已下线)8.5.3平面与平面平行(练案)-2021-2022学年高一数学同步备课 (人教A版2019 必修第二册)2023版 湘教版(2019) 必修第二册 过关斩将 第4章 4.4 平面与平面的位置关系 4.4.1 平面与平面平行(已下线)模块一 专题5 立体几何初步(2)(人教B)(已下线)模块一 专题5 立体几何初步(2)(北师大版)(已下线)模块一 专题3 立体几何初步(2)(人教A)(已下线)模块一 专题5 立体几何初步(2)(苏教版)(已下线)第03讲 直线、平面平行的判定与性质(八大题型)(讲义)(已下线)艺体生一轮复习 第七章 立体几何 第33讲 空间中的平行关系【练】 (已下线)第10讲 8.5.3 平面与平面平行-【帮课堂】(人教A版2019必修第二册)(已下线)第一章 点线面位置关系 专题一 空间平行关系的判定与证明 微点2 空间直线平行的判定与证明综合训练【基础版】(已下线)8.5空间直线、平面的平行——课堂例题(已下线)8.5.3 平面与平面平行-同步题型分类归纳讲与练(人教A版2019必修第二册)(已下线)11.3.3平面与平面平行-同步精品课堂(人教B版2019必修第四册)【课后练】 4.4.1 .2平面与平面平行的性质 课后作业-湘教版(2019)必修(第二册)第4章 立体几何初步
解题方法
4 . 已知平面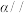 平面
平面 ,直线
,直线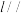 平面
平面 ,且点
,且点 ,
,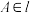 ,求证:
,求证: .
.
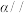 平面
平面 ,直线
,直线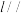 平面
平面 ,且点
,且点 ,
,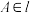 ,求证:
,求证: .
.
您最近一年使用:0次
名校
解题方法
5 . 已知底面边长和斜高长均为2的正四棱锥 被平行于底面的平面所截得的正棱台为
被平行于底面的平面所截得的正棱台为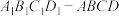 ,且满足
,且满足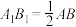 .
.
(1)求证:
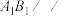 平面
平面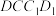
(2)求棱台的体积
 和表面积
和表面积 .
.
您最近一年使用:0次
名校
6 . 如图,矩形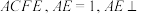 平面
平面
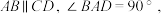
 ,平面
,平面 与棱
与棱 交于点G.
交于点G.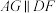 ;
;
(2)求直线 与平面
与平面 夹角的正弦值;
夹角的正弦值;
(3)求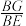 的值.
的值.
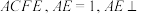 平面
平面
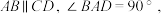
 ,平面
,平面 与棱
与棱 交于点G.
交于点G.
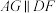 ;
;(2)求直线
 与平面
与平面 夹角的正弦值;
夹角的正弦值;(3)求
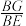 的值.
的值.
您最近一年使用:0次
2022-10-26更新
|
782次组卷
|
2卷引用:北京市丰台区第十二中学2021-2022学年高二上学期期中数学试题
名校
7 . 如图,在多面体 中,平面
中,平面 平面
平面 .四边形
.四边形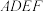 为正方形,四边形
为正方形,四边形 为梯形,且
为梯形,且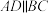 ,
,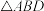 是边长为1的等边三角形,
是边长为1的等边三角形, 为线段
为线段 三等分点(靠近点
三等分点(靠近点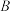 ),
), .
.

(1)求证: ;
;
(2)求直线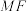 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)线段 上是否存在点
上是否存在点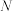 ,使得直线
,使得直线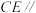 平面
平面 ?若存在,求
?若存在,求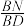 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 中,平面
中,平面 平面
平面 .四边形
.四边形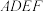 为正方形,四边形
为正方形,四边形 为梯形,且
为梯形,且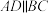 ,
,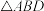 是边长为1的等边三角形,
是边长为1的等边三角形, 为线段
为线段 三等分点(靠近点
三等分点(靠近点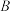 ),
), .
.
(1)求证:
 ;
;(2)求直线
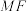 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)线段
 上是否存在点
上是否存在点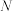 ,使得直线
,使得直线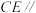 平面
平面 ?若存在,求
?若存在,求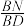 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2022-10-26更新
|
919次组卷
|
2卷引用:福建省泉州第一中学2021-2022学年高二上学期期中考试数学试题
2022高三·全国·专题练习
解题方法
8 . 在三棱柱 中,
中,
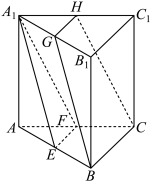
(1)若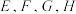 分别是
分别是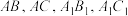 的中点,求证:平面
的中点,求证:平面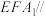 平面
平面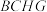 .
.
(2)若点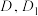 分别是
分别是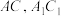 上的点,且平面
上的点,且平面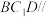 平面
平面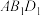 ,试求
,试求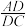 的值.
的值.
 中,
中,
(1)若
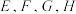 分别是
分别是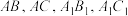 的中点,求证:平面
的中点,求证:平面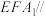 平面
平面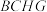 .
.(2)若点
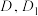 分别是
分别是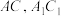 上的点,且平面
上的点,且平面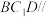 平面
平面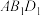 ,试求
,试求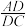 的值.
的值.
您最近一年使用:0次
2022-09-14更新
|
1079次组卷
|
11卷引用:第10课时 课中 空间中平面与平面的平行
(已下线)第10课时 课中 空间中平面与平面的平行(已下线)考点47 直线与平面、平面与平面平行-备战2022年高考数学一轮复习考点帮(新高考地区专用)【学科网名师堂】(已下线)7.1 空间几何中的平行(精练)(已下线)第03讲 空间直线、平面的平行 (精讲)-2(已下线)第47讲 直线与平面、平面与平面平行(已下线)第八章立体几何初步章末题型大总结(精讲)(2)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)8.5.3 平面与平面平行(1)-2022-2023学年高一数学《考点·题型·技巧》精讲与精练高分突破系列(人教A版2019必修第二册)(已下线)期末复习06 空间几何线面、面面平行-期末专项复习4.4.1 平面与平面平行(已下线)专题6-3立体几何大题综合归类-1(已下线)8.5.3 平面与平面平行 (第1课时) 平面与平面平行的判定(分层作业)-【上好课】
解题方法
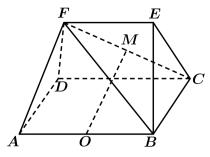
9 . 如图所示,已知多面体ABCDFE中,四边形ABCD为矩形, ,
, ,平面
,平面 平面ABCD,O,M分别为AB,FC的中点.
平面ABCD,O,M分别为AB,FC的中点.
(1)求证: ;
;
(2)求证: 平面DAF;
平面DAF;
(3)若过EF的平面交BC于点G,交AD于点H,求证: .
.
 ,
, ,平面
,平面 平面ABCD,O,M分别为AB,FC的中点.
平面ABCD,O,M分别为AB,FC的中点.
(1)求证:
 ;
;(2)求证:
 平面DAF;
平面DAF;(3)若过EF的平面交BC于点G,交AD于点H,求证:
 .
.
您最近一年使用:0次
解题方法
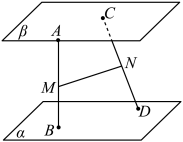
10 . 如图所示,两条异面直线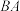 ,
, 与两平行平面
与两平行平面 ,
, 分别交于点
分别交于点 ,
, 和
和 ,
, ,点
,点 ,
, 分别是
分别是 ,
, 的中点,求证:
的中点,求证: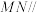 平面
平面
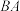 ,
, 与两平行平面
与两平行平面 ,
, 分别交于点
分别交于点 ,
, 和
和 ,
, ,点
,点 ,
, 分别是
分别是 ,
, 的中点,求证:
的中点,求证: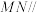 平面
平面

您最近一年使用:0次



