名校
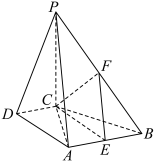
1 . 如图,在四棱锥 中,
中, 平面
平面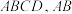

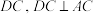 .
.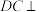 平面
平面 ;
;
(2)若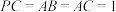 ,求
,求 与平面
与平面 成角的正弦值;
成角的正弦值;
(3)设点 为
为 的中点,过点
的中点,过点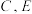 的平面与棱
的平面与棱 交于点
交于点 ,且
,且
 平面
平面 ,求
,求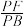 的值.
的值.
 中,
中, 平面
平面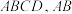

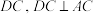 .
.
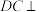 平面
平面 ;
;(2)若
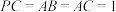 ,求
,求 与平面
与平面 成角的正弦值;
成角的正弦值;(3)设点
 为
为 的中点,过点
的中点,过点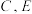 的平面与棱
的平面与棱 交于点
交于点 ,且
,且
 平面
平面 ,求
,求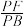 的值.
的值.
您最近一年使用:0次
2024-10-12更新
|
679次组卷
|
3卷引用:辽宁省七校2024-2025学年高二上学期期初考试数学试卷
2 . 如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形,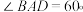 ,
, ,
, 为
为 的中点.
的中点. 平面
平面 ;
;
(2)若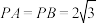 ,
,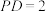 .
.
①求二面角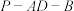 的余弦值;
的余弦值;
②求直线 与平面
与平面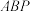 所成角的正弦值.
所成角的正弦值.
 中,底面
中,底面 为菱形,
为菱形,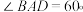 ,
, ,
, 为
为 的中点.
的中点.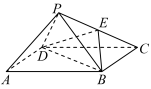
 平面
平面 ;
;(2)若
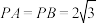 ,
,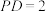 .
.①求二面角
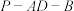 的余弦值;
的余弦值;②求直线
 与平面
与平面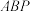 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
名校
3 . 如图,已知四边形 为菱形,四边形
为菱形,四边形 为平行四边形,且
为平行四边形,且 ,
,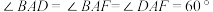 .
. 平面
平面 ;
;
(2)设平面 平面
平面 ,且二面角
,且二面角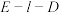 的平面角为
的平面角为 ,
,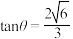 , 设
, 设 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 为菱形,四边形
为菱形,四边形 为平行四边形,且
为平行四边形,且 ,
,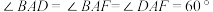 .
.
 平面
平面 ;
;(2)设平面
 平面
平面 ,且二面角
,且二面角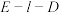 的平面角为
的平面角为 ,
,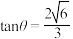 , 设
, 设 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-07-22更新
|
778次组卷
|
3卷引用:辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷
4 . 如图,在四棱柱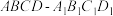 中,平面
中,平面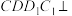 平面
平面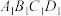 ,
,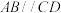 ,
, ,
,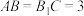 ,
,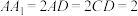 .
. 平面
平面 ;
;
(2)求直线 与平面
与平面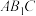 所成角的正弦值.
所成角的正弦值.
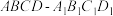 中,平面
中,平面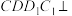 平面
平面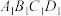 ,
,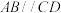 ,
, ,
,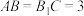 ,
,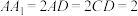 .
.
 平面
平面 ;
;(2)求直线
 与平面
与平面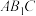 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-07-09更新
|
554次组卷
|
2卷引用:辽宁省辽阳市2023-2024学年高一下学期期末考试数学试卷
名校
5 . 如图在四棱锥 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱 ,且
,且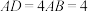 ,
, ,
,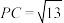 ,点E为AD中点,
,点E为AD中点, 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)点F为对角线AC上的点,且 ,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱 ,且
,且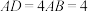 ,
, ,
,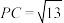 ,点E为AD中点,
,点E为AD中点,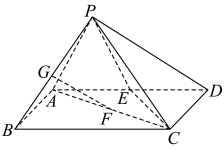
 平面
平面 ;
;(2)求二面角
 的余弦值;
的余弦值;(3)点F为对角线AC上的点,且
 ,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
您最近一年使用:0次
2024-06-23更新
|
860次组卷
|
4卷引用:辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷
辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷浙东北联盟(ZDB)四校2023-2024学年高一下学期期中考试数学试卷(已下线)第3套 全真模拟卷 (中等)【高一期末复习全真模拟】河南省信阳市息县第二高级中学联考2023-2024学年高一下学期7月期末考试数学试题
名校
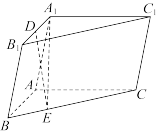
6 . 如图,三棱柱 中,侧面
中,侧面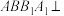 底面
底面 ,
,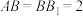 ,
,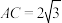 ,
,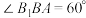 ,点
,点 是棱
是棱 的中点,
的中点, ,
, .
. ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,侧面
中,侧面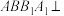 底面
底面 ,
,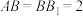 ,
,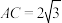 ,
,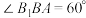 ,点
,点 是棱
是棱 的中点,
的中点, ,
, .
.
 ;
;(2)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-04-26更新
|
2645次组卷
|
5卷引用:辽宁省锦州市某校2023-2024学年高三下学期考前测试数学试卷(A)
辽宁省锦州市某校2023-2024学年高三下学期考前测试数学试卷(A)湖北省武汉市2024届高三下学期四月调考数学试卷2024届山东省五莲县第一中学高考模拟(二)数学试题河北省张家口市尚义县第一中学等校2024届高三下学期模拟演练数学试题(已下线)专题01 空间向量与立体几何解答题必考题型(6类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)
2024高三·全国·专题练习
名校
7 . 如图,四面体 中,
中, ,
, ,
, ,
, 为
为 的中点.
的中点.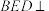 平面
平面 ;
;
(2)设 ,
,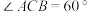 ,点
,点 在
在 上;
上;
①点 为
为 中点,求
中点,求 与
与 所成角的余弦值;
所成角的余弦值;
②当 的面积最小时,求
的面积最小时,求 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
 中,
中, ,
, ,
, ,
, 为
为 的中点.
的中点.
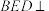 平面
平面 ;
;(2)设
 ,
,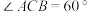 ,点
,点 在
在 上;
上;①点
 为
为 中点,求
中点,求 与
与 所成角的余弦值;
所成角的余弦值;②当
 的面积最小时,求
的面积最小时,求 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
您最近一年使用:0次
2024-03-18更新
|
1737次组卷
|
5卷引用:辽宁省五校联考2023-2024学年高一下学期期末考试数学试卷
辽宁省五校联考2023-2024学年高一下学期期末考试数学试卷(已下线)第二章 立体几何中的计算 专题一 空间角 微点5 直线与平面所成角综合训练【培优版】山西省临汾市侯马市第一中学校2023-2024学年高一下学期第三次月考数学试题江西省宜春市丰城市第九中学2023-2024学年高一下学期7月期末考试数学试题辽宁省鞍山市第一中学等校2023-2024学年高一下学期7月期末考试数学试题
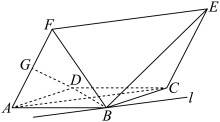
8 . 如图①,在平面四边形ABDC中, ,
,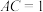 ,
,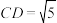 ,
,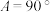 ,
, 将△BCD沿BC折起,形成如图②所示的三棱锥
将△BCD沿BC折起,形成如图②所示的三棱锥 ,且
,且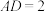 .
.
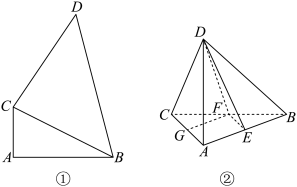
(1)证明: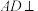 平面ABC;
平面ABC;
(2)在三棱锥 中,E,F,G分别为线段AB,BC,AC的中点,设平面DEF与平面DAC的交线为l,Q为l上的点,求直线DE与平面QFG所成角的正弦值的取值范围.
中,E,F,G分别为线段AB,BC,AC的中点,设平面DEF与平面DAC的交线为l,Q为l上的点,求直线DE与平面QFG所成角的正弦值的取值范围.
 ,
,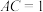 ,
,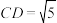 ,
,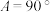 ,
, 将△BCD沿BC折起,形成如图②所示的三棱锥
将△BCD沿BC折起,形成如图②所示的三棱锥 ,且
,且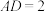 .
.
(1)证明:
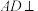 平面ABC;
平面ABC;(2)在三棱锥
 中,E,F,G分别为线段AB,BC,AC的中点,设平面DEF与平面DAC的交线为l,Q为l上的点,求直线DE与平面QFG所成角的正弦值的取值范围.
中,E,F,G分别为线段AB,BC,AC的中点,设平面DEF与平面DAC的交线为l,Q为l上的点,求直线DE与平面QFG所成角的正弦值的取值范围.
您最近一年使用:0次
2023-10-14更新
|
604次组卷
|
4卷引用:辽宁省名校联盟2023-2024学年高二上学期10月联合考试数学试题
辽宁省名校联盟2023-2024学年高二上学期10月联合考试数学试题江西省广丰贞白中学2024届高三上学期11月月考数学试题(已下线)考点16 立体几何中的最值问题 2024届高考数学考点总动员【讲】福建省泉州市晋江学校2023-2024学年高二上学期第二次月考数学试题
名校
9 . 如图,在堑堵 中(注:堑堵是一长方体沿不在同一面上的相对两棱斜解所得的几何体,即两底面为直角三角形的直三棱柱,最早的文字记载见于《九章算术》商功章),已知
中(注:堑堵是一长方体沿不在同一面上的相对两棱斜解所得的几何体,即两底面为直角三角形的直三棱柱,最早的文字记载见于《九章算术》商功章),已知 平面
平面 ,
,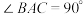 ,
, ,点
,点 、
、 分别是线段
分别是线段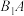 、
、 的中点.
的中点.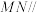 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
 中(注:堑堵是一长方体沿不在同一面上的相对两棱斜解所得的几何体,即两底面为直角三角形的直三棱柱,最早的文字记载见于《九章算术》商功章),已知
中(注:堑堵是一长方体沿不在同一面上的相对两棱斜解所得的几何体,即两底面为直角三角形的直三棱柱,最早的文字记载见于《九章算术》商功章),已知 平面
平面 ,
,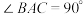 ,
, ,点
,点 、
、 分别是线段
分别是线段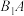 、
、 的中点.
的中点.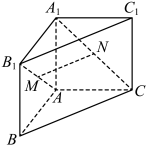
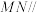 平面
平面 ;
;(2)求直线
 与平面
与平面 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
2023-08-02更新
|
1132次组卷
|
8卷引用:辽宁省朝阳市建平县实验中学2023-2024学年高二上学期期中数学试题
辽宁省朝阳市建平县实验中学2023-2024学年高二上学期期中数学试题浙江省宁波市慈溪市2022-2023学年高一下学期期末数学试题(已下线)压轴题立体几何新定义题(九省联考第19题模式)练(已下线)第四章 立体几何解题通法 专题二 升维法 微点3 升维法综合训练【培优版】(已下线)第六章 突破立体几何创新问题 专题一 交汇中国古代文化 微点1 与中国古代文化遗产有关的立体几何问题(一)【基础版】(已下线)重难点专题13 轻松搞定线面角问题-【帮课堂】(苏教版2019必修第二册)(已下线)专题08立体几何期末14种常考题型归类(1)-期末真题分类汇编(人教B版2019必修第四册)青海省西宁市第十四中学2023-2024学年高一下学期6月月考数学试卷
解题方法
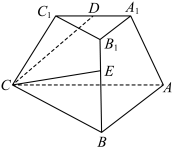
10 . 在正三棱台 中,
中, ,
,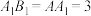 ,
, 为
为 中点,
中点, 在
在 上,
上, .
. 与平面
与平面 的交点
的交点 ,并写出
,并写出 与
与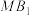 的比值(在图中保留作图痕迹,不必写出画法和理由);
的比值(在图中保留作图痕迹,不必写出画法和理由);
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, ,
,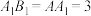 ,
, 为
为 中点,
中点, 在
在 上,
上, .
.
 与平面
与平面 的交点
的交点 ,并写出
,并写出 与
与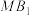 的比值(在图中保留作图痕迹,不必写出画法和理由);
的比值(在图中保留作图痕迹,不必写出画法和理由);(2)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2023-08-02更新
|
1724次组卷
|
6卷引用:辽宁省大连市2022-2023学年高一下学期期末数学试题
辽宁省大连市2022-2023学年高一下学期期末数学试题广东省阳江市2024届高三上学期开学适应性考试数学试题(已下线)重难点突破02 利用传统方法求线线角、线面角、二面角与距离(四大题型)(已下线)第八章 立体几何初步(压轴题专练)-单元速记·巧练(人教A版2019必修第二册)(已下线)重难点专题13 轻松搞定线面角问题-【帮课堂】(苏教版2019必修第二册)(已下线)专题02 高一下期末真题精选(2)-期末考点大串讲(人教A版2019必修第二册)



