1 . 已知直线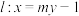 ,圆
,圆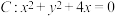 .
.
(1)证明:直线l与圆C相交;
(2)设l与C的两个交点分别为A、B,弦AB的中点为M,求点M的轨迹方程;
(3)在(2)的条件下,设圆C在点A处的切线为 ,在点B处的切线为
,在点B处的切线为 ,
, 与
与 的交点为Q.试探究:当m变化时,点Q是否恒在一条定直线上?若是,请求出这条直线的方程;若不是,说明理由.
的交点为Q.试探究:当m变化时,点Q是否恒在一条定直线上?若是,请求出这条直线的方程;若不是,说明理由.
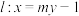 ,圆
,圆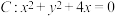 .
.(1)证明:直线l与圆C相交;
(2)设l与C的两个交点分别为A、B,弦AB的中点为M,求点M的轨迹方程;
(3)在(2)的条件下,设圆C在点A处的切线为
 ,在点B处的切线为
,在点B处的切线为 ,
, 与
与 的交点为Q.试探究:当m变化时,点Q是否恒在一条定直线上?若是,请求出这条直线的方程;若不是,说明理由.
的交点为Q.试探究:当m变化时,点Q是否恒在一条定直线上?若是,请求出这条直线的方程;若不是,说明理由.
您最近一年使用:0次
2022-01-22更新
|
3951次组卷
|
20卷引用:黑龙江省哈尔滨师范大学附属中学2023-2024学年高二上学期10月月考数学试题
黑龙江省哈尔滨师范大学附属中学2023-2024学年高二上学期10月月考数学试题上海市曹杨第二中学2021-2022学年高二上学期期末数学试题四川省遂宁中学校2021-2022学年高二下学期开学考试数学(理)试题四川省遂宁中学校2021-2022学年高二下学期开学考试数学(文)试题(已下线)专题26 求动点轨迹方程 微点7 求动点轨迹方程综合训练江苏省盐城市大丰区南阳中学2022-2023学年高二上学期第二次学情检测数学试题(已下线)专题18 直线和圆的方程(练习)-2北京市昌平区前锋学校2022-2023学年高二上学期期中考试数学试题浙江省台州市书生中学2023-2024学年高二上学期起始考数学试题(已下线)高二上学期第一次月考解答题压轴题50题专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)专题05 直线与圆综合大题18种题型归类-【巅峰课堂】2023-2024学年高二数学上学期期中期末复习讲练测(人教A版2019选择性必修第一册)(已下线)人教A版高二上学期【第一次月考卷】(测试范围:第1章-第2章)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线)第二章 直线与圆的方程(压轴必刷30题5种题型专项训练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线)期末真题必刷压轴60题(22个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)期末真题必刷常考60题(32个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)第2章 圆与方程单元检测卷(提优卷)-2023-2024学年高二数学《重难点题型·高分突破》(苏教版2019选择性必修第一册)(已下线)上海市高二下学期期末真题必刷04(压轴题)--高二期末考点大串讲(沪教版2020选修)(已下线)专题06 圆中定点定值问题四种考法-【常考压轴题】(苏教版2019选择性必修第一册)江西省新余市第十六中学2024-2025学年高二上学期第一次月考数学试卷安徽省蚌埠市五河第一中学2024-2025学年高二上学期第二次月考检测数学试题
2 . 已知圆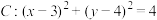 .
.
(1)若直线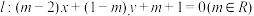 ,证明:无论
,证明:无论 为何值,直线
为何值,直线 都与圆
都与圆 相交;
相交;
(2)若过点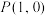 的直线
的直线 与圆
与圆 相交于
相交于 两点,求
两点,求 的面积的最大值,并求此时直线
的面积的最大值,并求此时直线 的方程.
的方程.
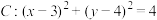 .
.(1)若直线
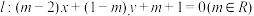 ,证明:无论
,证明:无论 为何值,直线
为何值,直线 都与圆
都与圆 相交;
相交;(2)若过点
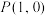 的直线
的直线 与圆
与圆 相交于
相交于 两点,求
两点,求 的面积的最大值,并求此时直线
的面积的最大值,并求此时直线 的方程.
的方程.
您最近一年使用:0次
2022-04-08更新
|
1536次组卷
|
7卷引用:黑龙江省鸡西市虎林市高级中学2022-2023学年高二上学期9月月考数学试题
黑龙江省鸡西市虎林市高级中学2022-2023学年高二上学期9月月考数学试题重庆市两江中学校(教育集团)2021-2022学年高二上学期第一次月考数学试题(已下线)第14讲 直线与圆、圆与圆的位置关系-【暑假自学课】2022年新高二数学暑假精品课(人教版2019必修第二册+选择性必修第一册)广东省普宁市华侨中学2022-2023学年高二上学期期中数学试题四川省眉山市眉山北外附属东坡外国语学校2022-2023学年高二上学期9月月考数学试题四川省成都市双流区双流中学2023-2024学年高二上学期10月月考数学试题湖南省雅礼集团2024-2025学年高二下学期第一次月考数学试卷
3 . 已知直线 :
: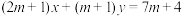 ,圆
,圆 :
: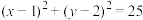
(1)求证:直线 与圆
与圆 总相交;
总相交;
(2)求出相交的弦长的最小值及相应的 值;
值;
 :
: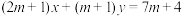 ,圆
,圆 :
: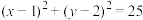
(1)求证:直线
 与圆
与圆 总相交;
总相交;(2)求出相交的弦长的最小值及相应的
 值;
值;
您最近一年使用:0次
2018-01-27更新
|
1388次组卷
|
3卷引用:黑龙江省鹤岗市第一中学2019-2020学年高二9月月考数学(文)试题
4 . 已知圆 与圆
与圆 :
: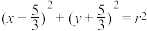 关于直线
关于直线 对称,且点
对称,且点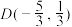 在圆
在圆 上.
上.
(1)判断圆 与圆
与圆 的公切线的条数;
的公切线的条数;
(2)设 为圆
为圆 上任意一点,
上任意一点,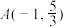 ,
,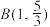 ,
,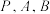 三点不共线,
三点不共线,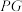 为
为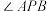 的平分线,且交
的平分线,且交 于
于 ,求证:
,求证: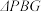 与
与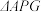 的面积之比为定值.
的面积之比为定值.
 与圆
与圆 :
: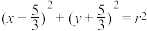 关于直线
关于直线 对称,且点
对称,且点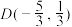 在圆
在圆 上.
上.(1)判断圆
 与圆
与圆 的公切线的条数;
的公切线的条数;(2)设
 为圆
为圆 上任意一点,
上任意一点,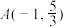 ,
,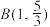 ,
,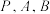 三点不共线,
三点不共线,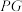 为
为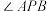 的平分线,且交
的平分线,且交 于
于 ,求证:
,求证: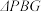 与
与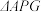 的面积之比为定值.
的面积之比为定值.
您最近一年使用:0次
2017-03-12更新
|
1375次组卷
|
3卷引用:黑龙江省穆棱市2016-2017学年高一下学期期末考试数学试卷.



