1 . 已知直线l: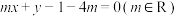 ,圆C:
,圆C: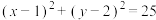 .
.
(1)求证不论m取何值,直线l与圆C恒相交;
(2)若直线l被圆C截得的弦长为8,求l的方程.
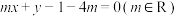 ,圆C:
,圆C: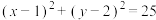 .
.(1)求证不论m取何值,直线l与圆C恒相交;
(2)若直线l被圆C截得的弦长为8,求l的方程.
您最近一年使用:0次
2023-01-06更新
|
226次组卷
|
3卷引用:安徽省安庆市岳西中学2023-2024学年高二上学期10月月考数学试题
2 . 已知直线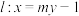 ,圆
,圆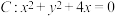 .
.
(1)证明:直线l与圆C相交;
(2)设l与C的两个交点分别为A、B,弦AB的中点为M,求点M的轨迹方程;
(3)在(2)的条件下,设圆C在点A处的切线为 ,在点B处的切线为
,在点B处的切线为 ,
, 与
与 的交点为Q.试探究:当m变化时,点Q是否恒在一条定直线上?若是,请求出这条直线的方程;若不是,说明理由.
的交点为Q.试探究:当m变化时,点Q是否恒在一条定直线上?若是,请求出这条直线的方程;若不是,说明理由.
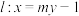 ,圆
,圆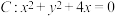 .
.(1)证明:直线l与圆C相交;
(2)设l与C的两个交点分别为A、B,弦AB的中点为M,求点M的轨迹方程;
(3)在(2)的条件下,设圆C在点A处的切线为
 ,在点B处的切线为
,在点B处的切线为 ,
, 与
与 的交点为Q.试探究:当m变化时,点Q是否恒在一条定直线上?若是,请求出这条直线的方程;若不是,说明理由.
的交点为Q.试探究:当m变化时,点Q是否恒在一条定直线上?若是,请求出这条直线的方程;若不是,说明理由.
您最近一年使用:0次
2022-01-22更新
|
3952次组卷
|
20卷引用:安徽省蚌埠市五河第一中学2024-2025学年高二上学期第二次月考检测数学试题
安徽省蚌埠市五河第一中学2024-2025学年高二上学期第二次月考检测数学试题上海市曹杨第二中学2021-2022学年高二上学期期末数学试题四川省遂宁中学校2021-2022学年高二下学期开学考试数学(理)试题四川省遂宁中学校2021-2022学年高二下学期开学考试数学(文)试题(已下线)专题26 求动点轨迹方程 微点7 求动点轨迹方程综合训练江苏省盐城市大丰区南阳中学2022-2023学年高二上学期第二次学情检测数学试题(已下线)专题18 直线和圆的方程(练习)-2北京市昌平区前锋学校2022-2023学年高二上学期期中考试数学试题浙江省台州市书生中学2023-2024学年高二上学期起始考数学试题(已下线)高二上学期第一次月考解答题压轴题50题专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)黑龙江省哈尔滨师范大学附属中学2023-2024学年高二上学期10月月考数学试题(已下线)专题05 直线与圆综合大题18种题型归类-【巅峰课堂】2023-2024学年高二数学上学期期中期末复习讲练测(人教A版2019选择性必修第一册)(已下线)人教A版高二上学期【第一次月考卷】(测试范围:第1章-第2章)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线)第二章 直线与圆的方程(压轴必刷30题5种题型专项训练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线)期末真题必刷压轴60题(22个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)期末真题必刷常考60题(32个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)第2章 圆与方程单元检测卷(提优卷)-2023-2024学年高二数学《重难点题型·高分突破》(苏教版2019选择性必修第一册)(已下线)上海市高二下学期期末真题必刷04(压轴题)--高二期末考点大串讲(沪教版2020选修)(已下线)专题06 圆中定点定值问题四种考法-【常考压轴题】(苏教版2019选择性必修第一册)江西省新余市第十六中学2024-2025学年高二上学期第一次月考数学试卷
21-22高二·全国·单元测试
解题方法
3 . 已知点 ,圆
,圆 :
: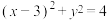 .
.
(1)判断点 与圆
与圆 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当 时,经过点
时,经过点 的直线
的直线 与圆相切,求直线
与圆相切,求直线 的方程;
的方程;
(3)若经过点 的直线与圆
的直线与圆 交于
交于 、
、 两点,且点
两点,且点 为
为 的中点,求点
的中点,求点 横坐标的取值范围.
横坐标的取值范围.
 ,圆
,圆 :
: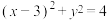 .
.(1)判断点
 与圆
与圆 的位置关系,并加以证明;
的位置关系,并加以证明;(2)当
 时,经过点
时,经过点 的直线
的直线 与圆相切,求直线
与圆相切,求直线 的方程;
的方程;(3)若经过点
 的直线与圆
的直线与圆 交于
交于 、
、 两点,且点
两点,且点 为
为 的中点,求点
的中点,求点 横坐标的取值范围.
横坐标的取值范围.
您最近一年使用:0次
2022-09-27更新
|
493次组卷
|
6卷引用:安徽省滁州市定远县第二中学2022-2023学年高二下学期期中数学试卷
安徽省滁州市定远县第二中学2022-2023学年高二下学期期中数学试卷(已下线)专题2.18 直线和圆的方程全章综合测试卷-2021-2022学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)专题2.17 直线和圆的方程大题专项训练(30道)-2021-2022学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)期末综合检测卷一 -2021-2022学年高二数学同步单元AB卷(人教A版2019选择性必修第一册)内蒙古呼和浩特市赛罕区英华学校2021-2022学年高一下学期期中考试数学试题(已下线)专题2.17 直线与圆的方程大题专项训练(30道)-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)
4 . 已知抛物线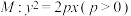 .
.
(1)设 为抛物线
为抛物线 上横坐标为1的定点,
上横坐标为1的定点, 为圆
为圆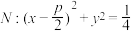 的一个动点,若
的一个动点,若 无公共点,且
无公共点,且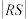 的最小值为
的最小值为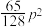 ,求
,求 的值;
的值;
(2)已知 分别是抛物线的一条弦,且都不与
分别是抛物线的一条弦,且都不与 轴垂直,
轴垂直, 与
与 相交于点
相交于点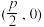 ,
,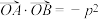 ,若四边形
,若四边形 的四条边都存在斜率且
的四条边都存在斜率且 ,求证:
,求证: .
.
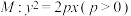 .
.(1)设
 为抛物线
为抛物线 上横坐标为1的定点,
上横坐标为1的定点, 为圆
为圆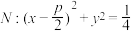 的一个动点,若
的一个动点,若 无公共点,且
无公共点,且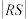 的最小值为
的最小值为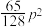 ,求
,求 的值;
的值;(2)已知
 分别是抛物线的一条弦,且都不与
分别是抛物线的一条弦,且都不与 轴垂直,
轴垂直, 与
与 相交于点
相交于点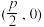 ,
,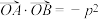 ,若四边形
,若四边形 的四条边都存在斜率且
的四条边都存在斜率且 ,求证:
,求证: .
.
您最近一年使用:0次
名校
5 . 如图,圆 :
: 交
交 轴于点
轴于点 ,
, (点
(点 在
在 轴的负半轴上),点
轴的负半轴上),点 为圆
为圆 上一动点,
上一动点, 、
、 分别交直线
分别交直线 于
于 ,
, 两点.
两点.
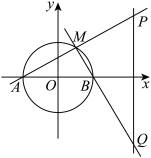
(1)证明: ,
, 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(2)若点 的坐标为
的坐标为 ,判断点
,判断点 与以
与以 为直径的圆的位置关系,并说明理由.
为直径的圆的位置关系,并说明理由.
 :
: 交
交 轴于点
轴于点 ,
, (点
(点 在
在 轴的负半轴上),点
轴的负半轴上),点 为圆
为圆 上一动点,
上一动点, 、
、 分别交直线
分别交直线 于
于 ,
, 两点.
两点.
(1)证明:
 ,
, 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;(2)若点
 的坐标为
的坐标为 ,判断点
,判断点 与以
与以 为直径的圆的位置关系,并说明理由.
为直径的圆的位置关系,并说明理由.
您最近一年使用:0次
2020-02-29更新
|
129次组卷
|
2卷引用:安徽省淮北市第一中学2018-2019学年高一下学期第三次月考数学(理)试题
名校
6 . 已知椭圆 的离心率为
的离心率为 ,且椭圆过点(1,
,且椭圆过点(1, )
)
(1)求椭圆 的方程;
的方程;
(2)设 是圆
是圆 上任一点,由
上任一点,由 引椭圆两条切线
引椭圆两条切线 ,当切线斜率存在时,求证两条斜率的积为定值.
,当切线斜率存在时,求证两条斜率的积为定值.
 的离心率为
的离心率为 ,且椭圆过点(1,
,且椭圆过点(1, )
)(1)求椭圆
 的方程;
的方程;
(2)设
 是圆
是圆 上任一点,由
上任一点,由 引椭圆两条切线
引椭圆两条切线 ,当切线斜率存在时,求证两条斜率的积为定值.
,当切线斜率存在时,求证两条斜率的积为定值.
您最近一年使用:0次
2018-10-19更新
|
1134次组卷
|
3卷引用:【市级联考】安徽省安庆市2018-2019学年高二第一学期期末教学质量调研检测理科数学试题



