1 . 过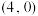 的直线与
的直线与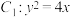 交于
交于 ,
, 两点,直线
两点,直线 、
、 与
与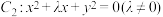 分别交于
分别交于 、
、 .
.
(1)证明: 中点在
中点在 轴上;
轴上;
(2)若 、
、 、
、 、
、 四点共圆,求
四点共圆,求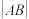 所有可能取值.
所有可能取值.
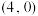 的直线与
的直线与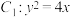 交于
交于 ,
, 两点,直线
两点,直线 、
、 与
与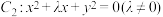 分别交于
分别交于 、
、 .
.(1)证明:
 中点在
中点在 轴上;
轴上;(2)若
 、
、 、
、 、
、 四点共圆,求
四点共圆,求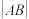 所有可能取值.
所有可能取值.
您最近一年使用:0次
2 . 已知直线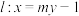 ,圆
,圆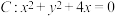 .
.
(1)证明:直线l与圆C相交;
(2)设l与C的两个交点分别为A、B,弦AB的中点为M,求点M的轨迹方程;
(3)在(2)的条件下,设圆C在点A处的切线为 ,在点B处的切线为
,在点B处的切线为 ,
, 与
与 的交点为Q.试探究:当m变化时,点Q是否恒在一条定直线上?若是,请求出这条直线的方程;若不是,说明理由.
的交点为Q.试探究:当m变化时,点Q是否恒在一条定直线上?若是,请求出这条直线的方程;若不是,说明理由.
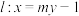 ,圆
,圆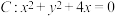 .
.(1)证明:直线l与圆C相交;
(2)设l与C的两个交点分别为A、B,弦AB的中点为M,求点M的轨迹方程;
(3)在(2)的条件下,设圆C在点A处的切线为
 ,在点B处的切线为
,在点B处的切线为 ,
, 与
与 的交点为Q.试探究:当m变化时,点Q是否恒在一条定直线上?若是,请求出这条直线的方程;若不是,说明理由.
的交点为Q.试探究:当m变化时,点Q是否恒在一条定直线上?若是,请求出这条直线的方程;若不是,说明理由.
您最近一年使用:0次
2022-01-22更新
|
3951次组卷
|
20卷引用:浙江省台州市书生中学2023-2024学年高二上学期起始考数学试题
浙江省台州市书生中学2023-2024学年高二上学期起始考数学试题上海市曹杨第二中学2021-2022学年高二上学期期末数学试题四川省遂宁中学校2021-2022学年高二下学期开学考试数学(理)试题四川省遂宁中学校2021-2022学年高二下学期开学考试数学(文)试题(已下线)专题26 求动点轨迹方程 微点7 求动点轨迹方程综合训练江苏省盐城市大丰区南阳中学2022-2023学年高二上学期第二次学情检测数学试题(已下线)专题18 直线和圆的方程(练习)-2北京市昌平区前锋学校2022-2023学年高二上学期期中考试数学试题(已下线)高二上学期第一次月考解答题压轴题50题专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)黑龙江省哈尔滨师范大学附属中学2023-2024学年高二上学期10月月考数学试题(已下线)专题05 直线与圆综合大题18种题型归类-【巅峰课堂】2023-2024学年高二数学上学期期中期末复习讲练测(人教A版2019选择性必修第一册)(已下线)人教A版高二上学期【第一次月考卷】(测试范围:第1章-第2章)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线)第二章 直线与圆的方程(压轴必刷30题5种题型专项训练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线)期末真题必刷压轴60题(22个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)期末真题必刷常考60题(32个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)第2章 圆与方程单元检测卷(提优卷)-2023-2024学年高二数学《重难点题型·高分突破》(苏教版2019选择性必修第一册)(已下线)上海市高二下学期期末真题必刷04(压轴题)--高二期末考点大串讲(沪教版2020选修)(已下线)专题06 圆中定点定值问题四种考法-【常考压轴题】(苏教版2019选择性必修第一册)江西省新余市第十六中学2024-2025学年高二上学期第一次月考数学试卷安徽省蚌埠市五河第一中学2024-2025学年高二上学期第二次月考检测数学试题
10-11高二上·贵州黔西·期末
名校
解题方法
3 . 已知圆 ,直线
,直线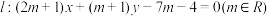 .
.
(1)证明:不论m取什么实数,直线 l 与圆恒交于两点;
(2)求直线被圆C 截得的弦长最小时 l 的方程.
 ,直线
,直线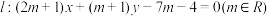 .
.(1)证明:不论m取什么实数,直线 l 与圆恒交于两点;
(2)求直线被圆C 截得的弦长最小时 l 的方程.
您最近一年使用:0次
2022-04-20更新
|
3902次组卷
|
45卷引用:浙江省金华市兰溪市厚仁中学2021-2022学年高二上学期期中数学试题
浙江省金华市兰溪市厚仁中学2021-2022学年高二上学期期中数学试题浙江省温州市“十五校联合体”2018-2019学年高二上学期期中联考数学试题浙江省宁波市鄞州中学2023-2024学年高二上学期期中考试数学试题(已下线)2010年贵州省册亨民族中学高二上学期末考试数学卷(已下线)2011-2012学年吉林省长春市高一上学期期末考试理科数学试卷(已下线)2012年人教A版高中数学必修二4.2直线、圆的位置关系练习卷(一)(已下线)2012-2013学年吉林省扶余一中高一上学期期末考试理科数学试卷(已下线)2013-2014学年江西南昌八一、中学、麻丘中学高二10月联考数学卷(已下线)2014届高考数学总复习考点引领+技巧点拨第九章第5课时练习卷2015-2016学年江西玉山一中高一下第一次月考理科数学卷2016-2017学年湖北白水高级中学高二9月月考数学试卷2016-2017学年山西怀仁县一中高二文上月考一数学试卷吉林省扶余市第一中学2016-2017学年高一下学期期末考试数学(理)试题新课标人教A版高中数学必修二第四章第2节《直线与圆的位置关系》专题练习江苏省如皋中学201810高二数学(文科)月考试题活页作业25 直线与圆的位置关系-2018年数学同步优化指导(北师大版必修2)(已下线)步步高高一数学寒假作业:作业18 直线、圆的位置关系沪教版(上海) 高三年级 新高考辅导与训练 第十一章 圆锥曲线 一、圆江苏省盐城市东台创新高级中学2019-2020学年高一下学期5月检测数学试题江西省南昌市新建一中2020-2021学年高二上学期第一次月考数学(理)试题江西省宜春市上高二中2021-2022学年高二上学期9月第一次月考数学(文)试题西藏拉萨中学2018-2019学年高一下学期期中数学试题(已下线)2.5.1 直线与圆的位置关系(分层练习)-2021-2022学年高二数学教材配套学案+课件+练习(人教A版2019选择性必修第一册)四川省内江市威远中学校2021-2022学年高二上学期期中考试数学(理科)试题四川省内江市威远中学校2021-2022学年高二上学期期中考试数学(文科)试题(已下线)考点37 直线与圆的方程-备战2022年高考数学典型试题解读与变式沪教版(2020) 选修第一册 领航者 第2章 2.1圆 第3课时 直线与圆的位置关系(已下线)第2章 圆与方程 单元综合检测(难点)四川省南充市南部县第二中学2021-2022学年高二下学期5月月考数学(理)试题(已下线)专题35 圆的方程-3圆的弦长与圆心距(已下线)2.2 直线与圆的位置关系(3)(已下线)专题18 直线和圆的方程(练习)-2四川省宜宾市叙州区第一中学校2022-2023学年高二上学期期中考试数学(文)试题四川省宜宾市叙州区第一中学校2022-2023学年高二上学期期中考试数学(理)试题(已下线)第12讲 直线与圆压轴题精选(2)1.2.3 直线与圆的位置关系 同步练习-2022-2023学年高二上学期数学北师大版(2019)选择性必修第一册江西省九江外国语学校2023-2024学年高二上学期第一次月考数学试题辽宁省辽东南协作校2023-2024学年高二上学期10月月考数学(A卷)试题山西省大同市第三中学校2024届高三上学期十月月考数学试题辽宁省鞍山市普通高中2023-2024学年高二上学期10月月考数学(A卷)试题湖南省娄底市涟源市第二中学2023-2024学年高二上学期10月月考数学试题云南省曲靖市师宗平高学校2023-2024学年高二上学期10月月考数学试题【随堂练】2.1.4 直线与圆的位置关系 随堂练习-沪教版(2020)选择性必修第一册第2章 圆锥曲线【课堂例】2.1.3直线与圆的位置关系 课堂例题 沪教版(2020)选择性必修第一册 第2章 圆锥曲线
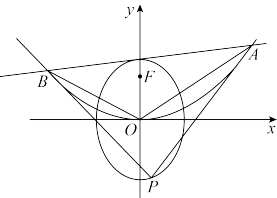
4 . 如图,已知椭圆 :
: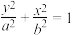 (
( )的离心率为
)的离心率为 ,并以抛物线
,并以抛物线 :
: 的焦点
的焦点 为上焦点.直线
为上焦点.直线 :
: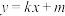 (
( )交抛物线
)交抛物线 于
于 ,
, 两点,分别以
两点,分别以 ,
, 为切点作抛物线
为切点作抛物线 的切线,两切线相交于点
的切线,两切线相交于点 ,又点
,又点 恰好在椭圆
恰好在椭圆 上.
上.
(1)求椭圆 的方程;
的方程;
(2)求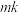 的最大值;
的最大值;
(3)求证:点 恒在
恒在 的外接圆内.
的外接圆内.
 :
: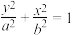 (
( )的离心率为
)的离心率为 ,并以抛物线
,并以抛物线 :
: 的焦点
的焦点 为上焦点.直线
为上焦点.直线 :
: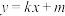 (
( )交抛物线
)交抛物线 于
于 ,
, 两点,分别以
两点,分别以 ,
, 为切点作抛物线
为切点作抛物线 的切线,两切线相交于点
的切线,两切线相交于点 ,又点
,又点 恰好在椭圆
恰好在椭圆 上.
上.
(1)求椭圆
 的方程;
的方程;(2)求
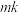 的最大值;
的最大值;(3)求证:点
 恒在
恒在 的外接圆内.
的外接圆内.
您最近一年使用:0次
19-20高二·浙江杭州·期末
5 . 已知圆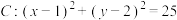 ,直线
,直线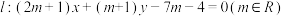 .
.
(1)证明:直线 过定点,且不论
过定点,且不论 取何值,直线
取何值,直线 与圆
与圆 总相交;
总相交;
(2)求直线被圆 截得线段的最短长度及此时
截得线段的最短长度及此时 的方程.
的方程.
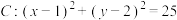 ,直线
,直线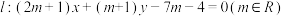 .
.(1)证明:直线
 过定点,且不论
过定点,且不论 取何值,直线
取何值,直线 与圆
与圆 总相交;
总相交;(2)求直线被圆
 截得线段的最短长度及此时
截得线段的最短长度及此时 的方程.
的方程.
您最近一年使用:0次



