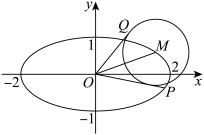
1 . 如图,在平面直角坐标系 中,设点
中,设点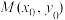 是椭圆C:
是椭圆C: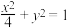 上一点,从原点O向圆
上一点,从原点O向圆 作两条切线,分别与椭圆C交于点
作两条切线,分别与椭圆C交于点 ,直线
,直线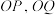 的斜率分别记为
的斜率分别记为 .
.
(1)若圆M与x轴相切于椭圆C的右焦点,求圆M的方程;
(2)若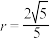 ,求证:
,求证: ;
;
(3)在(2)的情况下,求 的最大值.
的最大值.
 中,设点
中,设点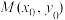 是椭圆C:
是椭圆C: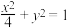 上一点,从原点O向圆
上一点,从原点O向圆 作两条切线,分别与椭圆C交于点
作两条切线,分别与椭圆C交于点 ,直线
,直线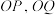 的斜率分别记为
的斜率分别记为 .
.
(1)若圆M与x轴相切于椭圆C的右焦点,求圆M的方程;
(2)若
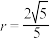 ,求证:
,求证: ;
;(3)在(2)的情况下,求
 的最大值.
的最大值.
您最近一年使用:0次
2023-09-12更新
|
1181次组卷
|
6卷引用:专题9.8 直线与圆锥曲线位置关系(练)-江苏版《2020年高考一轮复习讲练测》
(已下线)专题9.8 直线与圆锥曲线位置关系(练)-江苏版《2020年高考一轮复习讲练测》(已下线)专题06 椭圆的压轴题(6类题型+过关检测)-【常考压轴题】2023-2024学年高二数学上学期压轴题攻略(人教A版2019选择性必修第一册)2016届江苏省南京市、盐城市高三第一次模拟考试数学试卷2017届上海市复旦大学附属中学高三毕业考试数学试题山东省枣庄市滕州市第一中学2022-2023学年高二上学期期中数学试题云南省曲靖市第一中学2024届高三上学期阶段性检测(四)数学试题
2 . 已知以点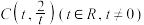 为圆心的圆与x轴交于点O,A,与y轴交于点O、B,其中O为坐标原点.
为圆心的圆与x轴交于点O,A,与y轴交于点O、B,其中O为坐标原点.
(1)试写出圆C的标准方程(含 表示);
表示);
(2)求证: 的面积为定值;
的面积为定值;
(3)设直线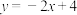 与圆C交于M,N两点,若
与圆C交于M,N两点,若 ,求圆C的标准方程.
,求圆C的标准方程.
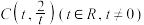 为圆心的圆与x轴交于点O,A,与y轴交于点O、B,其中O为坐标原点.
为圆心的圆与x轴交于点O,A,与y轴交于点O、B,其中O为坐标原点.(1)试写出圆C的标准方程(含
 表示);
表示);(2)求证:
 的面积为定值;
的面积为定值;(3)设直线
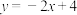 与圆C交于M,N两点,若
与圆C交于M,N两点,若 ,求圆C的标准方程.
,求圆C的标准方程.
您最近一年使用:0次
2022-04-24更新
|
1718次组卷
|
10卷引用:2.1 圆
(已下线)2.1 圆(已下线)第12讲 直线与圆压轴题精选(2)(已下线)专题05 圆的压轴题(2)四川省成都市石室中学2016-2017学年高一下学期半期考试数学试题广东省深圳市南山区华侨城中学2021-2022学年高二上学期期中数学试题沪教版(2020) 选修第一册 新课改一课一练 第2章 2.1.4直线与圆的位置关系黑龙江省大庆市第四中学2022-2023学年高二上学期第一次检测数学试题 (已下线)第08讲 圆的方程(3大考点九种解题方法)(1)(已下线)高二上学期第一次月考解答题压轴题50题专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)内蒙古通辽市开鲁县第一中学2021-2022学年高一下学期期中考试数学试题
名校
解题方法
3 . 已知圆 和
和 轴相切于点
轴相切于点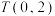 ,与
,与 轴的正半轴交于
轴的正半轴交于 、
、 两点(
两点( 在
在 的左侧),且
的左侧),且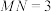 .
.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)过点 任作一条直线与圆
任作一条直线与圆 :
: 相交于点
相交于点 、
、 ,连接
,连接 和
和 ,记
,记 和
和 的斜率分别为
的斜率分别为 ,
, ,求证:
,求证: 为定值.
为定值.
 和
和 轴相切于点
轴相切于点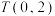 ,与
,与 轴的正半轴交于
轴的正半轴交于 、
、 两点(
两点( 在
在 的左侧),且
的左侧),且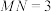 .
.(Ⅰ)求圆
 的方程;
的方程;(Ⅱ)过点
 任作一条直线与圆
任作一条直线与圆 :
: 相交于点
相交于点 、
、 ,连接
,连接 和
和 ,记
,记 和
和 的斜率分别为
的斜率分别为 ,
, ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
2021-01-26更新
|
553次组卷
|
7卷引用:天津市静海县第一中学2017-2018学年高二上学期期末终结性检测数学(理)试题
天津市静海县第一中学2017-2018学年高二上学期期末终结性检测数学(理)试题(已下线)专题9.4 直线与圆、圆与圆的位置关系-2021年高考数学(理)一轮复习-题型全归纳与高效训练突破(已下线)专题09 与圆有关的定值问题-【重难点突破】2021-2022学年高二数学上册常考题专练(人教A版2019选择性必修第一册)贵州省遵义市第四中学2016届高三上学期第四次月考数学(文)试题江苏省扬州中学2019-2020学年高一下学期4月阶段测试数学试题陕西省咸阳市2020-2021学年高一上学期期末数学试题山西大学附属中学2022届高三上学期11月期中数学(文)试题
名校
解题方法
4 . 如图,已知圆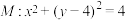 ,直线
,直线 的方程为
的方程为 ,点
,点 是直线
是直线 上一动点,过点
上一动点,过点 作圆的切线
作圆的切线 、
、 ,切点为
,切点为 、
、 .
.

(1)当 的横坐标为
的横坐标为 时,求
时,求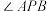 的大小;
的大小;
(2)求证:经过 、
、 、
、 三点的圆
三点的圆 必过定点,并求出所有定点的坐标.
必过定点,并求出所有定点的坐标.
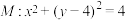 ,直线
,直线 的方程为
的方程为 ,点
,点 是直线
是直线 上一动点,过点
上一动点,过点 作圆的切线
作圆的切线 、
、 ,切点为
,切点为 、
、 .
.
(1)当
 的横坐标为
的横坐标为 时,求
时,求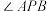 的大小;
的大小;(2)求证:经过
 、
、 、
、 三点的圆
三点的圆 必过定点,并求出所有定点的坐标.
必过定点,并求出所有定点的坐标.
您最近一年使用:0次
名校
解题方法
5 . 给定椭圆 ,称圆心在原点
,称圆心在原点 、半径为
、半径为 的圆是椭圆
的圆是椭圆 的“卫星圆”,若椭圆
的“卫星圆”,若椭圆 的离心率为
的离心率为 ,点
,点 在
在 上.
上.
(1)求椭圆 的方程和其“卫星圆”方程;
的方程和其“卫星圆”方程;
(2)点 是椭圆
是椭圆 的“卫星圆”上的一个动点,过点
的“卫星圆”上的一个动点,过点 作直线
作直线 、
、 使得
使得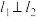 ,与椭圆
,与椭圆 都只有一个交点,且
都只有一个交点,且 、
、 分别交其“卫星圆”于点
分别交其“卫星圆”于点 、
、 ,证明:弦长
,证明:弦长 为定值.
为定值.
 ,称圆心在原点
,称圆心在原点 、半径为
、半径为 的圆是椭圆
的圆是椭圆 的“卫星圆”,若椭圆
的“卫星圆”,若椭圆 的离心率为
的离心率为 ,点
,点 在
在 上.
上.(1)求椭圆
 的方程和其“卫星圆”方程;
的方程和其“卫星圆”方程;(2)点
 是椭圆
是椭圆 的“卫星圆”上的一个动点,过点
的“卫星圆”上的一个动点,过点 作直线
作直线 、
、 使得
使得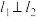 ,与椭圆
,与椭圆 都只有一个交点,且
都只有一个交点,且 、
、 分别交其“卫星圆”于点
分别交其“卫星圆”于点 、
、 ,证明:弦长
,证明:弦长 为定值.
为定值.
您最近一年使用:0次
2020-08-05更新
|
1226次组卷
|
17卷引用:冲刺卷01-决战2020年高考数学冲刺卷(山东专版)
(已下线)冲刺卷01-决战2020年高考数学冲刺卷(山东专版)(已下线)提升套餐练01-【新题型】2020年新高考数学多选题与热点解答题组合练(已下线)第8篇——平面解析几何-新高考山东专题汇编(已下线)强化卷01(4月)-冲刺2020高考数学之拿高分题目强化卷(山东专版)(已下线)专题16 圆锥曲线常考题型04——定值问题-【重难点突破】2021-2022学年高二数学上册常考题专练(人教A版2019选择性必修第一册)山东省青岛市实验高中(青岛第十五中学)2020-2021学年高二上学期期中考试数学试题(已下线)重组5 高二期中真题重组卷(湖北卷)A基础卷2020届山东省青岛市高三上学期期末数学试题2020届山东省潍坊市奎文区第一中学高三下学期3月月考数学试题2020届山东省菏泽一中高三下学期在线数学试题2020届山东省菏泽一中高三2月份自测数学试题山东省济钢高中2019-2020学年高三3月质量检测试题(已下线)大题专练训练28:圆锥曲线(切线问题)-2021届高三数学二轮复习广东省东莞市石竹实验学校2022-2023学年高二下学期开学学情调查数学试题辽宁省朝阳市建平县实验中学2023-2024学年高二下学期6月月考数学试题重庆市缙云教育联盟2022届高三上学期9月月度质量检测数学试题山东省潍坊市昌乐第一中学2024届高三上学期模拟预测数学试题
名校
解题方法
6 . 在平面直角坐标系 中,已知以点
中,已知以点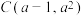 (
( )为圆心的圆过原点O,不过圆心C的直线
)为圆心的圆过原点O,不过圆心C的直线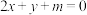 (
(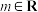 )与圆C交于M,N两点,且点
)与圆C交于M,N两点,且点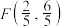 为线段
为线段 的中点.
的中点.
(1)求m的值和圆C的方程;
(2)若Q是直线 上的动点,直线
上的动点,直线 ,
,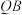 分别切圆C于A,B两点,求证:直线
分别切圆C于A,B两点,求证:直线 恒过定点;
恒过定点;
(3)若过点 (
(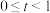 )的直线L与圆C交于D,E两点,对于每一个确定的t,当
)的直线L与圆C交于D,E两点,对于每一个确定的t,当 的面积最大时,记直线l的斜率的平方为u,试用含t的代数式表示u,并求u的最大值.
的面积最大时,记直线l的斜率的平方为u,试用含t的代数式表示u,并求u的最大值.
 中,已知以点
中,已知以点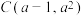 (
( )为圆心的圆过原点O,不过圆心C的直线
)为圆心的圆过原点O,不过圆心C的直线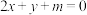 (
(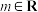 )与圆C交于M,N两点,且点
)与圆C交于M,N两点,且点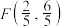 为线段
为线段 的中点.
的中点.(1)求m的值和圆C的方程;
(2)若Q是直线
 上的动点,直线
上的动点,直线 ,
,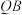 分别切圆C于A,B两点,求证:直线
分别切圆C于A,B两点,求证:直线 恒过定点;
恒过定点;(3)若过点
 (
(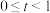 )的直线L与圆C交于D,E两点,对于每一个确定的t,当
)的直线L与圆C交于D,E两点,对于每一个确定的t,当 的面积最大时,记直线l的斜率的平方为u,试用含t的代数式表示u,并求u的最大值.
的面积最大时,记直线l的斜率的平方为u,试用含t的代数式表示u,并求u的最大值.
您最近一年使用:0次
2020-09-17更新
|
1169次组卷
|
6卷引用:福建师范大学附属中学2020-2021学年高二上学期期中考试数学试题
福建师范大学附属中学2020-2021学年高二上学期期中考试数学试题天津市南开中学2020-2021学年高二上学期期中数学试题(已下线)专题20 《圆与方程》中的周长与面积问题(1)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)(已下线)专题05 《圆与方程》中的压轴题(1)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)广东省广东实验中学2019-2020学年高一下学期期中数学试题(已下线)卷06 直线与圆的方程-单元检测(难)(原卷版)-2021-2022学年高二数学单元卷模拟(易中难)(2019人教A版选择性必修第一册+第二册)
名校
7 . 在平面直角坐标系xOy中,圆C的圆心在直线x+y-3=0上,圆C经过点A(0,4),且与直线3x-4y+16=0相切.
(1)求圆C的方程;
(2)设直线l交圆C于P,Q两点,若直线AP,AQ的斜率之积为2,求证:直线l过一个定点,并求出该定点坐标.
(1)求圆C的方程;
(2)设直线l交圆C于P,Q两点,若直线AP,AQ的斜率之积为2,求证:直线l过一个定点,并求出该定点坐标.
您最近一年使用:0次
2020-08-05更新
|
346次组卷
|
3卷引用:重组9 高二期中真题重组卷(安徽卷)B提升卷
名校
8 . 已知椭圆 :
: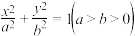 ,
, ,
,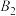 分别是椭圆短轴的上下两个端点,
分别是椭圆短轴的上下两个端点, 是椭圆的左焦点,P是椭圆上异于点
是椭圆的左焦点,P是椭圆上异于点 ,
,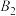 的点,若
的点,若 的边长为4的等边三角形.
的边长为4的等边三角形.
 写出椭圆的标准方程;
写出椭圆的标准方程;
 当直线
当直线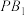 的一个方向向量是
的一个方向向量是 时,求以
时,求以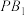 为直径的圆的标准方程;
为直径的圆的标准方程;
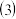 设点R满足:
设点R满足: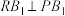 ,
,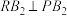 ,求证:
,求证: 与
与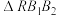 的面积之比为定值.
的面积之比为定值.
 :
: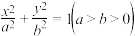 ,
, ,
,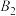 分别是椭圆短轴的上下两个端点,
分别是椭圆短轴的上下两个端点, 是椭圆的左焦点,P是椭圆上异于点
是椭圆的左焦点,P是椭圆上异于点 ,
,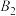 的点,若
的点,若 的边长为4的等边三角形.
的边长为4的等边三角形. 写出椭圆的标准方程;
写出椭圆的标准方程; 当直线
当直线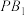 的一个方向向量是
的一个方向向量是 时,求以
时,求以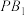 为直径的圆的标准方程;
为直径的圆的标准方程;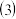 设点R满足:
设点R满足: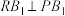 ,
,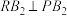 ,求证:
,求证: 与
与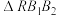 的面积之比为定值.
的面积之比为定值.
您最近一年使用:0次
2019-11-08更新
|
478次组卷
|
6卷引用:上海市华东师范大学第三附属中学2019-2020学年高二上学期12月月考数学试题
上海市华东师范大学第三附属中学2019-2020学年高二上学期12月月考数学试题(已下线)专题05 平面解析几何-2020年高三数学(理)3-4月模拟试题汇编(已下线)专题02圆锥曲线全章复习攻略--高二期末考点大串讲(沪教版2020选修一)2019年上海市崇明区高三上学期期末(一模)数学试题2020届湖南省长沙市明达中学高三(高复部)第二次模拟考试理科数学试题(已下线)专题02 圆锥曲线--高二期末考点大串讲(沪教版2020选修)
9 . 已知圆 的圆心在直线
的圆心在直线 上,并且经过点
上,并且经过点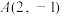 ,与直线
,与直线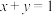 相切.
相切.
(1)试求圆 的方程;
的方程;
(2)若圆 与直线
与直线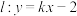 相交于
相交于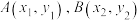 两点.求证:
两点.求证: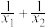 为定值.
为定值.
 的圆心在直线
的圆心在直线 上,并且经过点
上,并且经过点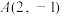 ,与直线
,与直线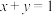 相切.
相切.(1)试求圆
 的方程;
的方程;(2)若圆
 与直线
与直线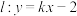 相交于
相交于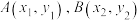 两点.求证:
两点.求证: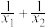 为定值.
为定值.
您最近一年使用:0次
名校
10 . 动圆 与
与 轴交于
轴交于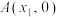 ,
, 两点,且
两点,且 是方程
是方程 的两根.
的两根.
(1)若线段 是动圆
是动圆 的直径,求动圆
的直径,求动圆 的方程;
的方程;
(2)证明:当动圆 过点
过点 时,动圆
时,动圆 在
在 轴上截得弦长为定值.
轴上截得弦长为定值.
 与
与 轴交于
轴交于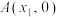 ,
, 两点,且
两点,且 是方程
是方程 的两根.
的两根.(1)若线段
 是动圆
是动圆 的直径,求动圆
的直径,求动圆 的方程;
的方程;(2)证明:当动圆
 过点
过点 时,动圆
时,动圆 在
在 轴上截得弦长为定值.
轴上截得弦长为定值.
您最近一年使用:0次
2020-05-20更新
|
599次组卷
|
9卷引用:福建省厦门第一中学2020-2021学年高二分班摸底练习数学试题
福建省厦门第一中学2020-2021学年高二分班摸底练习数学试题(已下线)专题09 与圆有关的定值问题-【重难点突破】2021-2022学年高二数学上册常考题专练(人教A版2019选择性必修第一册)福建省厦门第一中学2020-2021学年高二上学期摸底考试数学试题2020届广东省高三普通高中招生全国统一考试模拟(一)数学(文)试题苏教版(2019) 选修第一册 突围者 第2章 专项拓展训练2 与圆有关的定点、定值、探索性问题山东省日照第一中学2021-2022学年高二上学期第一次月考数学试题(已下线)专题2.17 直线和圆的方程大题专项训练(30道)-2021-2022学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)2.3 圆与圆的位置关系-高二数学同步精品课堂(苏教版2019选择性必修第一册)内蒙古通辽实验中学2020-2021学年高一上学期自主检测数学理科试题



