1 . 已知 中,直线
中,直线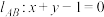 过
过 两点,点
两点,点 在
在 轴上,且
轴上,且 为正三角形.
为正三角形.
(1)求过 的直线方程;
的直线方程;
(2)设过 两点的直线
两点的直线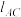 斜率为
斜率为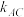 ,过A,B两点的直线
,过A,B两点的直线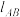 斜率为
斜率为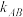 ,且
,且 ,
,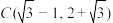 ,且圆
,且圆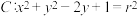 与
与 有且只有2个交点,求r的取值范围.
有且只有2个交点,求r的取值范围.
 中,直线
中,直线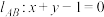 过
过 两点,点
两点,点 在
在 轴上,且
轴上,且 为正三角形.
为正三角形.(1)求过
 的直线方程;
的直线方程;(2)设过
 两点的直线
两点的直线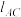 斜率为
斜率为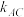 ,过A,B两点的直线
,过A,B两点的直线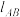 斜率为
斜率为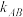 ,且
,且 ,
,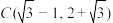 ,且圆
,且圆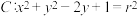 与
与 有且只有2个交点,求r的取值范围.
有且只有2个交点,求r的取值范围.
您最近半年使用:0次
名校
解题方法
2 . 已知半径为 的圆
的圆 的圆心在
的圆心在 轴的正半轴上,且直线
轴的正半轴上,且直线 与圆
与圆 相切.
相切.
(1)求圆 的标准方程;
的标准方程;
(2)若 的坐标为
的坐标为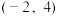 ,过点
,过点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 ,求直线
,求直线 的方程;
的方程;
(3)过点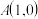 任作一条不与
任作一条不与 轴垂直的直线与圆
轴垂直的直线与圆 相交于
相交于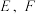 两点,在
两点,在 非正半轴上是否存在点
非正半轴上是否存在点 ,使得
,使得 ?若存在,求点
?若存在,求点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 的圆
的圆 的圆心在
的圆心在 轴的正半轴上,且直线
轴的正半轴上,且直线 与圆
与圆 相切.
相切.(1)求圆
 的标准方程;
的标准方程;(2)若
 的坐标为
的坐标为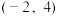 ,过点
,过点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 ,求直线
,求直线 的方程;
的方程;(3)过点
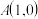 任作一条不与
任作一条不与 轴垂直的直线与圆
轴垂直的直线与圆 相交于
相交于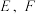 两点,在
两点,在 非正半轴上是否存在点
非正半轴上是否存在点 ,使得
,使得 ?若存在,求点
?若存在,求点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
您最近半年使用:0次
2024-01-08更新
|
270次组卷
|
2卷引用:福建省泉州市第七中学2023-2024学年高二上学期期中考试数学试卷
解题方法
3 . 已知圆C: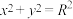 与圆
与圆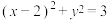 的相交弦长为
的相交弦长为
(1)求圆C的半径R的值;
(2)若对于 的圆,已知点
的圆,已知点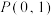 ,点
,点 ,
, 在圆C上,直线
在圆C上,直线 不经过点
不经过点 ,且直线
,且直线 ,
, 的斜率之和为2,求证:直线MN经过一定点,并求出该定点的坐标.
的斜率之和为2,求证:直线MN经过一定点,并求出该定点的坐标.
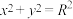 与圆
与圆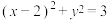 的相交弦长为
的相交弦长为

(1)求圆C的半径R的值;
(2)若对于
 的圆,已知点
的圆,已知点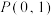 ,点
,点 ,
, 在圆C上,直线
在圆C上,直线 不经过点
不经过点 ,且直线
,且直线 ,
, 的斜率之和为2,求证:直线MN经过一定点,并求出该定点的坐标.
的斜率之和为2,求证:直线MN经过一定点,并求出该定点的坐标.
您最近半年使用:0次
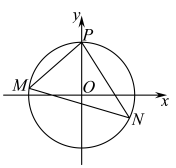
4 . 如图,一个湖的边界是圆心为 的圆,湖的一侧有一条直线型公路
的圆,湖的一侧有一条直线型公路 ,湖上有桥
,湖上有桥 (
( 是圆
是圆 的直径).规划在公路
的直径).规划在公路 上选两个点
上选两个点 ,
, (点
(点 在点
在点 的左侧),并修建两段直线型道路
的左侧),并修建两段直线型道路 ,
, ,规划要求:线段
,规划要求:线段 ,
, 上的所有点到点
上的所有点到点 的距离均不小于圆
的距离均不小于圆 的半径.已知点
的半径.已知点 ,
, 到直线
到直线 的距离分别为
的距离分别为 和
和 (
( ,
, 为垂足),测得
为垂足),测得 ,
, ,
, (单位,百米).
(单位,百米).
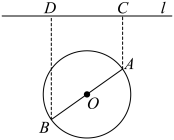
(1)若 点选在
点选在 点的左侧8百米处,则道路
点的左侧8百米处,则道路 是否符合规划要求?
是否符合规划要求?
(2)在规划要求下,求 的最小值.
的最小值.
 的圆,湖的一侧有一条直线型公路
的圆,湖的一侧有一条直线型公路 ,湖上有桥
,湖上有桥 (
( 是圆
是圆 的直径).规划在公路
的直径).规划在公路 上选两个点
上选两个点 ,
, (点
(点 在点
在点 的左侧),并修建两段直线型道路
的左侧),并修建两段直线型道路 ,
, ,规划要求:线段
,规划要求:线段 ,
, 上的所有点到点
上的所有点到点 的距离均不小于圆
的距离均不小于圆 的半径.已知点
的半径.已知点 ,
, 到直线
到直线 的距离分别为
的距离分别为 和
和 (
( ,
, 为垂足),测得
为垂足),测得 ,
, ,
, (单位,百米).
(单位,百米).
(1)若
 点选在
点选在 点的左侧8百米处,则道路
点的左侧8百米处,则道路 是否符合规划要求?
是否符合规划要求?(2)在规划要求下,求
 的最小值.
的最小值.
您最近半年使用:0次
名校
5 . 已知直线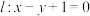 和圆
和圆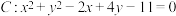 .
.
(1)若直线 交圆
交圆 于
于 两点,求弦
两点,求弦 的长;
的长;
(2)求过点 且与圆
且与圆 相切的直线方程.
相切的直线方程.
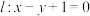 和圆
和圆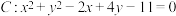 .
.(1)若直线
 交圆
交圆 于
于 两点,求弦
两点,求弦 的长;
的长;(2)求过点
 且与圆
且与圆 相切的直线方程.
相切的直线方程.
您最近半年使用:0次
2023-12-20更新
|
464次组卷
|
2卷引用:福建省莆田二中、仙游一中2023-2024学年高二上12月月考数学试卷
名校
解题方法
6 . 已知直线l: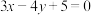 与圆C:
与圆C: 相切.
相切.
(1)求实数a的值;
(2)已知直线m: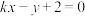 与圆C相交于A,B两点,若
与圆C相交于A,B两点,若 的面积为2,求直线m的方程.
的面积为2,求直线m的方程.
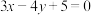 与圆C:
与圆C: 相切.
相切.(1)求实数a的值;
(2)已知直线m:
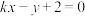 与圆C相交于A,B两点,若
与圆C相交于A,B两点,若 的面积为2,求直线m的方程.
的面积为2,求直线m的方程.
您最近半年使用:0次
2023-12-16更新
|
930次组卷
|
3卷引用:福建省华安县第一中学2023-2024学年高二上学期第二次月考(12月)数学试题
名校
解题方法
7 . 已知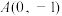 ,
,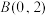 ,圆
,圆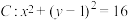 ,点
,点 在圆
在圆 上运动,动点
上运动,动点 满足
满足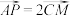 ,记动点
,记动点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求动点 的轨迹方程;
的轨迹方程;
(2)若过点 的直线
的直线 与曲线
与曲线 交于Q,R两点,且
交于Q,R两点,且 ,求直线
,求直线 的方程.
的方程.
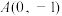 ,
,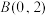 ,圆
,圆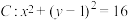 ,点
,点 在圆
在圆 上运动,动点
上运动,动点 满足
满足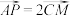 ,记动点
,记动点 的轨迹为曲线
的轨迹为曲线 .
.(1)求动点
 的轨迹方程;
的轨迹方程;(2)若过点
 的直线
的直线 与曲线
与曲线 交于Q,R两点,且
交于Q,R两点,且 ,求直线
,求直线 的方程.
的方程.
您最近半年使用:0次
8 . 在平面直角坐标系 中,已知点
中,已知点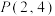 ,圆
,圆 :
: 与
与 轴的正半轴的交点是
轴的正半轴的交点是 ,过点
,过点 的直线
的直线 与圆
与圆 交于不同的两点
交于不同的两点 .
.
(1)设直线
 ,
,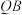 的斜率分别是
的斜率分别是 ,
, ,求
,求 的值;
的值;(2)设
 的中点为
的中点为 ,点
,点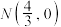 ,若
,若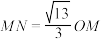 ,求
,求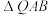 的面积.
的面积.
您最近半年使用:0次
名校
解题方法
9 . 已知圆 ,圆
,圆 :
: ,圆
,圆 :
: ,这三个圆有一条公共弦.
,这三个圆有一条公共弦.
(1)当圆 的面积最小时,求圆
的面积最小时,求圆 的标准方程;
的标准方程;
(2)在(1)的条件下,直线 同时满足以下三个条件:
同时满足以下三个条件:
(i)与直线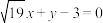 垂直;
垂直;
(ii)与圆 相切;
相切;
(iii)在 轴上的截距大于0,
轴上的截距大于0,
若直线 与圆
与圆 交于
交于 ,
, 两点,求
两点,求 .
.
 ,圆
,圆 :
: ,圆
,圆 :
: ,这三个圆有一条公共弦.
,这三个圆有一条公共弦.(1)当圆
 的面积最小时,求圆
的面积最小时,求圆 的标准方程;
的标准方程;(2)在(1)的条件下,直线
 同时满足以下三个条件:
同时满足以下三个条件:(i)与直线
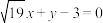 垂直;
垂直;(ii)与圆
 相切;
相切;(iii)在
 轴上的截距大于0,
轴上的截距大于0,若直线
 与圆
与圆 交于
交于 ,
, 两点,求
两点,求 .
.
您最近半年使用:0次
2023-11-12更新
|
303次组卷
|
3卷引用:福建省泉州市永春第一中学2023-2024学年高二上学期期中数学试题
10 . 已知直线l: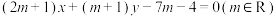 和圆C:
和圆C: .
.
(1)直线l恒过一定点M,求出点M坐标;
(2)当m为何值时,直线l被圆C所截得的弦长最短,求出弦长;
(3)在(2)的前提下,直线 是过点
是过点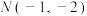 且与直线l平行的直线,求圆心在直线
且与直线l平行的直线,求圆心在直线 上,且与圆
上,且与圆 外切的动圆中半径最小的圆的标准方程.
外切的动圆中半径最小的圆的标准方程.
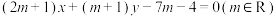 和圆C:
和圆C: .
.(1)直线l恒过一定点M,求出点M坐标;
(2)当m为何值时,直线l被圆C所截得的弦长最短,求出弦长;
(3)在(2)的前提下,直线
 是过点
是过点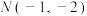 且与直线l平行的直线,求圆心在直线
且与直线l平行的直线,求圆心在直线 上,且与圆
上,且与圆 外切的动圆中半径最小的圆的标准方程.
外切的动圆中半径最小的圆的标准方程.
您最近半年使用:0次
2023-10-16更新
|
516次组卷
|
3卷引用:福建省莆田市锦江中学2023-2024学年高二上学期期中数学试题



