解题方法
1 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,过点
,过点 的动直线
的动直线 交
交 于A,B两点,点
于A,B两点,点 在
在 轴上方,且
轴上方,且 不与
不与 轴垂直,
轴垂直, 的周长为
的周长为 ,直线
,直线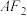 与
与 交于另一点
交于另一点 ,直线
,直线 与
与 交于另一点
交于另一点 ,点
,点 为椭圆
为椭圆 的下顶点,如图①.
的下顶点,如图①. 为椭圆
为椭圆 的上顶点时,将平面xOy沿
的上顶点时,将平面xOy沿 轴折叠如图②,使平面
轴折叠如图②,使平面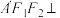 平面
平面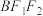 ,求异面直线
,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(2)若过 作
作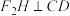 ,垂足为
,垂足为 .
.
(i)证明:直线 过定点;
过定点;
(ii)求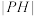 的最大值.
的最大值.
 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,过点
,过点 的动直线
的动直线 交
交 于A,B两点,点
于A,B两点,点 在
在 轴上方,且
轴上方,且 不与
不与 轴垂直,
轴垂直, 的周长为
的周长为 ,直线
,直线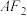 与
与 交于另一点
交于另一点 ,直线
,直线 与
与 交于另一点
交于另一点 ,点
,点 为椭圆
为椭圆 的下顶点,如图①.
的下顶点,如图①.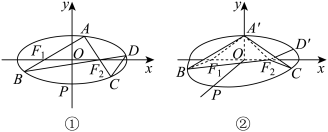
 为椭圆
为椭圆 的上顶点时,将平面xOy沿
的上顶点时,将平面xOy沿 轴折叠如图②,使平面
轴折叠如图②,使平面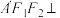 平面
平面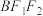 ,求异面直线
,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;(2)若过
 作
作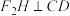 ,垂足为
,垂足为 .
.(i)证明:直线
 过定点;
过定点;(ii)求
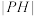 的最大值.
的最大值.
您最近一年使用:0次
2024-04-16更新
|
1696次组卷
|
4卷引用:湖北省恩施州巴东县2024届高三下学期教学质量检测(二)数学试题
湖北省恩施州巴东县2024届高三下学期教学质量检测(二)数学试题河北省石家庄市2024届高三下学期教学质量检测(二)数学试卷(已下线)压轴题02圆锥曲线压轴题17题型汇总-1(已下线)专题5 解析几何中的十一大名圆(二)【讲】
2 . 已知椭圆 经过点
经过点 ,且短轴长为2,经过点
,且短轴长为2,经过点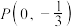 的直线
的直线 与椭圆
与椭圆 交于
交于 两点,且在
两点,且在 轴上存在点
轴上存在点 ,使得
,使得 .
.
(1)求椭圆 的方程;
的方程;
(2)求 面积的最大值.
面积的最大值.
 经过点
经过点 ,且短轴长为2,经过点
,且短轴长为2,经过点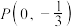 的直线
的直线 与椭圆
与椭圆 交于
交于 两点,且在
两点,且在 轴上存在点
轴上存在点 ,使得
,使得 .
.(1)求椭圆
 的方程;
的方程;(2)求
 面积的最大值.
面积的最大值.
您最近一年使用:0次
名校
解题方法
3 . 椭圆 的焦距为
的焦距为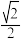 ,点
,点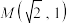 是椭圆
是椭圆 上一点,过点
上一点,过点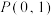 的动直线
的动直线 与椭圆相交于
与椭圆相交于 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)在平面直角坐标系 中,是否存在与点
中,是否存在与点 不同的定点
不同的定点 ,使
,使 恒成立?存在,求出点
恒成立?存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 的焦距为
的焦距为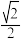 ,点
,点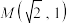 是椭圆
是椭圆 上一点,过点
上一点,过点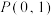 的动直线
的动直线 与椭圆相交于
与椭圆相交于 两点.
两点.(1)求椭圆
 的方程;
的方程;(2)在平面直角坐标系
 中,是否存在与点
中,是否存在与点 不同的定点
不同的定点 ,使
,使 恒成立?存在,求出点
恒成立?存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
您最近一年使用:0次
2023-11-21更新
|
356次组卷
|
2卷引用:湖北省恩施州巴东县第一高级中学2023-2024学年高二上学期第三次月考数学试题
名校
解题方法
4 . 已知椭圆 与直线
与直线 有唯一的公共点
有唯一的公共点 ,过点
,过点 且与
且与 垂直的直线
垂直的直线 交
交 轴,
轴, 轴于
轴于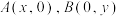 两点.
两点.
(1)求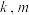 满足的关系式;
满足的关系式;
(2)当点 运动时,求点
运动时,求点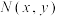 的轨迹
的轨迹 的方程;
的方程;
(3)若轨迹 与直线
与直线 交于
交于 两点,
两点, 为坐标原点,求
为坐标原点,求 面积的最大值.
面积的最大值.
 与直线
与直线 有唯一的公共点
有唯一的公共点 ,过点
,过点 且与
且与 垂直的直线
垂直的直线 交
交 轴,
轴, 轴于
轴于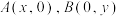 两点.
两点.(1)求
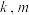 满足的关系式;
满足的关系式;(2)当点
 运动时,求点
运动时,求点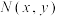 的轨迹
的轨迹 的方程;
的方程;(3)若轨迹
 与直线
与直线 交于
交于 两点,
两点, 为坐标原点,求
为坐标原点,求 面积的最大值.
面积的最大值.
您最近一年使用:0次
2023-09-27更新
|
565次组卷
|
4卷引用:湖北省恩施州高中教育联盟2022-2023学年高二下学期期中数学试题
湖北省恩施州高中教育联盟2022-2023学年高二下学期期中数学试题(已下线)专题3-2 椭圆大题综合11种题型归类(讲+练)-【巅峰课堂】2023-2024学年高二数学热点题型归纳与培优练(人教A版2019选择性必修第一册)河南省南阳市第一中学校2023-2024学年高二上学期第四次月考数学试题(已下线)第3章 圆锥曲线与方程章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第一册)
5 . 已知 是椭圆
是椭圆 的左右焦点,以
的左右焦点,以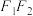 为直径的圆和椭圆
为直径的圆和椭圆 在第一象限的交点为
在第一象限的交点为 ,若三角形
,若三角形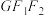 的面积为1,其内切圆的半径为
的面积为1,其内切圆的半径为 .
.
(1)求椭圆 的方程;
的方程;
(2)已知A是椭圆 的上顶点,过点
的上顶点,过点 的直线与椭圆
的直线与椭圆 交于不同的两点
交于不同的两点 ,点
,点 在第二象限,直线
在第二象限,直线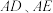 分别与
分别与 轴交于
轴交于 ,求四边形
,求四边形 面积的最大值.
面积的最大值.
 是椭圆
是椭圆 的左右焦点,以
的左右焦点,以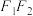 为直径的圆和椭圆
为直径的圆和椭圆 在第一象限的交点为
在第一象限的交点为 ,若三角形
,若三角形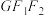 的面积为1,其内切圆的半径为
的面积为1,其内切圆的半径为 .
.(1)求椭圆
 的方程;
的方程;(2)已知A是椭圆
 的上顶点,过点
的上顶点,过点 的直线与椭圆
的直线与椭圆 交于不同的两点
交于不同的两点 ,点
,点 在第二象限,直线
在第二象限,直线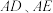 分别与
分别与 轴交于
轴交于 ,求四边形
,求四边形 面积的最大值.
面积的最大值.
您最近一年使用:0次
2023-06-01更新
|
915次组卷
|
5卷引用:湖北省恩施市第二中学2023届高三适应性考试数学试题
湖北省恩施市第二中学2023届高三适应性考试数学试题江西师范大学附属中学2023届高三三模考试数学(理)试题(已下线)第08讲 直线与圆锥曲线的位置关系(四大题型6个方向)(讲义)-2(已下线)专题10 圆锥曲线综合大题10种题型归类-【寒假分层作业】2024年高二数学寒假培优练(人教A版2019选择性必修第一册)(已下线)专题08 椭圆中最值范围五种考法-【常考压轴题】2024-2025学年高二数学压轴题攻略(苏教版2019选择性必修第一册)
名校
解题方法
6 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,过左焦点
,过左焦点 的直线
的直线 与椭圆
与椭圆 交于
交于 两点(
两点( 不在
不在 轴上),
轴上), 的周长为
的周长为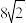 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若点 在椭圆
在椭圆 上,且
上,且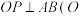 为坐标原点),求
为坐标原点),求 的取值范围.
的取值范围.
 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,过左焦点
,过左焦点 的直线
的直线 与椭圆
与椭圆 交于
交于 两点(
两点( 不在
不在 轴上),
轴上), 的周长为
的周长为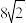 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若点
 在椭圆
在椭圆 上,且
上,且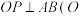 为坐标原点),求
为坐标原点),求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-02-14更新
|
754次组卷
|
7卷引用:湖北省恩施州巴东县第三高级中学2022-2023学年高二下学期第二次月考(3月)数学试题
名校
解题方法
7 . 已知椭圆 :
: 的离心率为
的离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,
, ,且
,且 到直线
到直线 :
: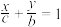 的距离为
的距离为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若直线 :
: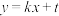 与椭圆
与椭圆 交于
交于 ,
, 两个不同的点,
两个不同的点, 为坐标原点,
为坐标原点, 是椭圆
是椭圆 上的一点,且四边形
上的一点,且四边形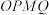 是平行四边形,求四边形
是平行四边形,求四边形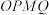 的面积.
的面积.
 :
: 的离心率为
的离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,
, ,且
,且 到直线
到直线 :
: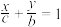 的距离为
的距离为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若直线
 :
: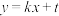 与椭圆
与椭圆 交于
交于 ,
, 两个不同的点,
两个不同的点, 为坐标原点,
为坐标原点, 是椭圆
是椭圆 上的一点,且四边形
上的一点,且四边形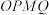 是平行四边形,求四边形
是平行四边形,求四边形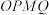 的面积.
的面积.
您最近一年使用:0次
2020-07-31更新
|
1050次组卷
|
6卷引用:湖北省恩施州2019-2020学年高二下学期期末数学试题
8 . 已知椭圆 的离心率为
的离心率为 ,点
,点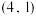 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)若直线上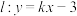 与C交于A,B两点,是否存在l,使得点
与C交于A,B两点,是否存在l,使得点 在以AB为直径的圆外.若存在,求出k的取值范围;若不存在,请说明理由.
在以AB为直径的圆外.若存在,求出k的取值范围;若不存在,请说明理由.
 的离心率为
的离心率为 ,点
,点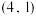 在椭圆C上.
在椭圆C上.(1)求椭圆C的标准方程;
(2)若直线上
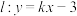 与C交于A,B两点,是否存在l,使得点
与C交于A,B两点,是否存在l,使得点 在以AB为直径的圆外.若存在,求出k的取值范围;若不存在,请说明理由.
在以AB为直径的圆外.若存在,求出k的取值范围;若不存在,请说明理由.
您最近一年使用:0次
2020-01-28更新
|
457次组卷
|
2卷引用:湖北省恩施州2020届高三上学期期末理科数学试题



