23-24高三上·江苏苏州·期末
名校
解题方法
1 . 在平面直角坐标系 中,已知椭圆
中,已知椭圆 经过点
经过点 ,直线
,直线 与
与 轴交于点
轴交于点 ,过
,过 的直线
的直线 与
与 交于
交于 两点(异于
两点(异于 ),记直线
),记直线 和直线
和直线 的斜率分别为
的斜率分别为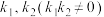 .
.
(1)求 的标准方程;
的标准方程;
(2)求 的值;
的值;
(3)设直线 和直线
和直线 的交点为
的交点为 ,求证:
,求证: 在一条定直线上.
在一条定直线上.
 中,已知椭圆
中,已知椭圆 经过点
经过点 ,直线
,直线 与
与 轴交于点
轴交于点 ,过
,过 的直线
的直线 与
与 交于
交于 两点(异于
两点(异于 ),记直线
),记直线 和直线
和直线 的斜率分别为
的斜率分别为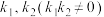 .
.(1)求
 的标准方程;
的标准方程;(2)求
 的值;
的值;(3)设直线
 和直线
和直线 的交点为
的交点为 ,求证:
,求证: 在一条定直线上.
在一条定直线上.
您最近一年使用:0次
2024-01-29更新
|
534次组卷
|
3卷引用:2.2.2 椭圆的性质(十八大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)
(已下线)2.2.2 椭圆的性质(十八大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)江苏省苏州市2024届高三上学期学业质量阳光指标调研数学试题山东省东营市第一中学2023-2024学年高二下学期开学收心考试数学试题
23-24高二上·湖北恩施·阶段练习
2 . 已知椭圆 经过点
经过点 ,且短轴长为2,经过点
,且短轴长为2,经过点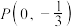 的直线
的直线 与椭圆
与椭圆 交于
交于 两点,且在
两点,且在 轴上存在点
轴上存在点 ,使得
,使得 .
.
(1)求椭圆 的方程;
的方程;
(2)求 面积的最大值.
面积的最大值.
 经过点
经过点 ,且短轴长为2,经过点
,且短轴长为2,经过点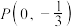 的直线
的直线 与椭圆
与椭圆 交于
交于 两点,且在
两点,且在 轴上存在点
轴上存在点 ,使得
,使得 .
.(1)求椭圆
 的方程;
的方程;(2)求
 面积的最大值.
面积的最大值.
您最近一年使用:0次
22-23高二下·上海·期末
3 . 已知椭圆 经过点
经过点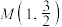 ,且其右焦点与抛物线
,且其右焦点与抛物线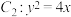 的焦点F重合,过点F且与坐标轴不垂直的直线与椭圆交于P,Q两点.
的焦点F重合,过点F且与坐标轴不垂直的直线与椭圆交于P,Q两点.
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点,线段 上是否存在点
上是否存在点 ,使得
,使得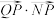 =
=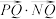 ?若存在,求出n的取值范围;若不存在,说明理由;
?若存在,求出n的取值范围;若不存在,说明理由;
(3)过点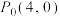 且不垂直于x轴的直线与椭圆交于A,B两点,点B关于x轴的对称点为E,试证明:直线
且不垂直于x轴的直线与椭圆交于A,B两点,点B关于x轴的对称点为E,试证明:直线 过定点.
过定点.
 经过点
经过点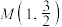 ,且其右焦点与抛物线
,且其右焦点与抛物线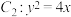 的焦点F重合,过点F且与坐标轴不垂直的直线与椭圆交于P,Q两点.
的焦点F重合,过点F且与坐标轴不垂直的直线与椭圆交于P,Q两点.(1)求椭圆
 的方程;
的方程;(2)设O为坐标原点,线段
 上是否存在点
上是否存在点 ,使得
,使得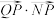 =
=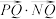 ?若存在,求出n的取值范围;若不存在,说明理由;
?若存在,求出n的取值范围;若不存在,说明理由;(3)过点
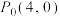 且不垂直于x轴的直线与椭圆交于A,B两点,点B关于x轴的对称点为E,试证明:直线
且不垂直于x轴的直线与椭圆交于A,B两点,点B关于x轴的对称点为E,试证明:直线 过定点.
过定点.
您最近一年使用:0次
名校
解题方法
4 . 已知椭圆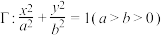 的左、右焦点分别为
的左、右焦点分别为 、
、 ,长轴长为4,
,长轴长为4, 是椭圆
是椭圆 上的一点,直线l的斜率为k,在y轴上的截距为m.
上的一点,直线l的斜率为k,在y轴上的截距为m.
(1)求椭圆 的标准方程;
的标准方程;
(2)设 ,直线l与椭圆
,直线l与椭圆 交于不同的两点A,B,O为坐标原点,求
交于不同的两点A,B,O为坐标原点,求 面积的最大值;
面积的最大值;
(3)设 是直线l的一个法向量,M是l上一点,对于坐标平面内的定点N,定义
是直线l的一个法向量,M是l上一点,对于坐标平面内的定点N,定义 .用a、b、k、m表示
.用a、b、k、m表示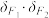 ,并利用
,并利用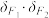 与
与 的大小关系,提出一个关于l与
的大小关系,提出一个关于l与 位置关系的真命题,给出命题的证明.
位置关系的真命题,给出命题的证明.
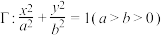 的左、右焦点分别为
的左、右焦点分别为 、
、 ,长轴长为4,
,长轴长为4, 是椭圆
是椭圆 上的一点,直线l的斜率为k,在y轴上的截距为m.
上的一点,直线l的斜率为k,在y轴上的截距为m.(1)求椭圆
 的标准方程;
的标准方程;(2)设
 ,直线l与椭圆
,直线l与椭圆 交于不同的两点A,B,O为坐标原点,求
交于不同的两点A,B,O为坐标原点,求 面积的最大值;
面积的最大值;(3)设
 是直线l的一个法向量,M是l上一点,对于坐标平面内的定点N,定义
是直线l的一个法向量,M是l上一点,对于坐标平面内的定点N,定义 .用a、b、k、m表示
.用a、b、k、m表示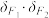 ,并利用
,并利用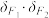 与
与 的大小关系,提出一个关于l与
的大小关系,提出一个关于l与 位置关系的真命题,给出命题的证明.
位置关系的真命题,给出命题的证明.
您最近一年使用:0次
解题方法
5 . 已知椭圆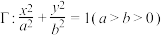 的焦距为2,且过点
的焦距为2,且过点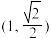 .
.

(1)求椭圆 的标准方程;
的标准方程;
(2) 、
、 分别为椭圆
分别为椭圆 的上、下顶点,
的上、下顶点, 为坐标原点,过椭圆
为坐标原点,过椭圆 的左焦点
的左焦点 作直线
作直线 交椭圆
交椭圆 于
于 、
、 两点,与
两点,与 轴交于
轴交于 点.
点.
①若点 是线段
是线段 的中点,求点
的中点,求点 的轨迹方程;
的轨迹方程;
②设直线 与直线
与直线 交于点
交于点 ,求证:
,求证: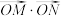 为定值.
为定值.
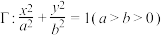 的焦距为2,且过点
的焦距为2,且过点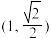 .
.
(1)求椭圆
 的标准方程;
的标准方程;(2)
 、
、 分别为椭圆
分别为椭圆 的上、下顶点,
的上、下顶点, 为坐标原点,过椭圆
为坐标原点,过椭圆 的左焦点
的左焦点 作直线
作直线 交椭圆
交椭圆 于
于 、
、 两点,与
两点,与 轴交于
轴交于 点.
点.①若点
 是线段
是线段 的中点,求点
的中点,求点 的轨迹方程;
的轨迹方程;②设直线
 与直线
与直线 交于点
交于点 ,求证:
,求证: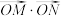 为定值.
为定值.
您最近一年使用:0次
2023-06-20更新
|
391次组卷
|
2卷引用:上海市宝山区2022-2023学年高二下学期期末数学试题
解题方法
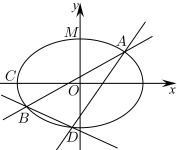
6 . 如图,已知点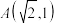 是椭圆
是椭圆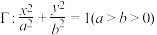 上的一点,顶点
上的一点,顶点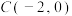 .
.
(1)求椭圆 的离心率;
的离心率;
(2)直线 交椭圆
交椭圆 于
于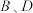 两点(
两点(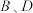 与
与 不重合),若直线
不重合),若直线 与直线
与直线 的斜率之和为2,直线
的斜率之和为2,直线 是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
(3)点 、点
、点 是椭圆
是椭圆 上的两个点,圆
上的两个点,圆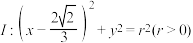 是
是 的内切圆,过椭圆
的内切圆,过椭圆 的顶点
的顶点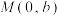 作圆
作圆 的两条切线,分别交椭圆
的两条切线,分别交椭圆 于点
于点 和点
和点 ,判断直线
,判断直线 与圆
与圆 的位置关系并证明.
的位置关系并证明.
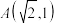 是椭圆
是椭圆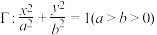 上的一点,顶点
上的一点,顶点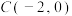 .
.
(1)求椭圆
 的离心率;
的离心率;(2)直线
 交椭圆
交椭圆 于
于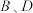 两点(
两点(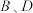 与
与 不重合),若直线
不重合),若直线 与直线
与直线 的斜率之和为2,直线
的斜率之和为2,直线 是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.(3)点
 、点
、点 是椭圆
是椭圆 上的两个点,圆
上的两个点,圆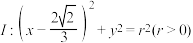 是
是 的内切圆,过椭圆
的内切圆,过椭圆 的顶点
的顶点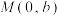 作圆
作圆 的两条切线,分别交椭圆
的两条切线,分别交椭圆 于点
于点 和点
和点 ,判断直线
,判断直线 与圆
与圆 的位置关系并证明.
的位置关系并证明.
您最近一年使用:0次
名校
解题方法
7 . 已知双曲线 ,点
,点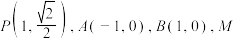 为双曲线上的动点.
为双曲线上的动点.
(1)求以 为焦点且经过点
为焦点且经过点 的椭圆的标准方程;
的椭圆的标准方程;
(2)若直线 经过点
经过点 且与双曲线恰好有一个公共点,求直线
且与双曲线恰好有一个公共点,求直线 的方程;
的方程;
(3)点 在什么位置时,
在什么位置时,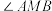 取得最大?求出最大值及点
取得最大?求出最大值及点 的坐标.
的坐标.
 ,点
,点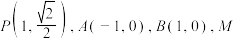 为双曲线上的动点.
为双曲线上的动点.(1)求以
 为焦点且经过点
为焦点且经过点 的椭圆的标准方程;
的椭圆的标准方程;(2)若直线
 经过点
经过点 且与双曲线恰好有一个公共点,求直线
且与双曲线恰好有一个公共点,求直线 的方程;
的方程;(3)点
 在什么位置时,
在什么位置时,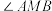 取得最大?求出最大值及点
取得最大?求出最大值及点 的坐标.
的坐标.
您最近一年使用:0次
2023-06-04更新
|
451次组卷
|
2卷引用:上海市宜川中学2023届高三5月模拟数学试题
名校
解题方法
8 . 已知平面直角坐标系 中,椭圆
中,椭圆 的方程为
的方程为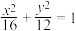 ,若
,若 上存在三个不同点
上存在三个不同点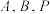 ,满足
,满足 .
.
(1)若 分别为
分别为 的右顶点与上顶点,且
的右顶点与上顶点,且 ,求
,求 的值;
的值;
(2)当 且
且 不垂直
不垂直 轴时,设直线
轴时,设直线 的方程为
的方程为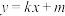 ,求
,求 与
与 之间的关系;
之间的关系;
(3)求实数 的取值范围.
的取值范围.
 中,椭圆
中,椭圆 的方程为
的方程为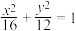 ,若
,若 上存在三个不同点
上存在三个不同点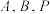 ,满足
,满足 .
.(1)若
 分别为
分别为 的右顶点与上顶点,且
的右顶点与上顶点,且 ,求
,求 的值;
的值;(2)当
 且
且 不垂直
不垂直 轴时,设直线
轴时,设直线 的方程为
的方程为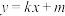 ,求
,求 与
与 之间的关系;
之间的关系;(3)求实数
 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
9 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为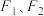 ,直线l的斜率为k,在y轴上的截距为m.
,直线l的斜率为k,在y轴上的截距为m.
(1)设 ,若
,若 的焦距为2,l过点
的焦距为2,l过点 ,求l的方程;
,求l的方程;
(2)设 ,若
,若 是
是 上的一点,且
上的一点,且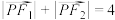 ,l与
,l与 交于不同的两点A、B,Q为
交于不同的两点A、B,Q为 的上顶点,求
的上顶点,求 面积的最大值;
面积的最大值;
(3)设 是l的一个法向量,M是l上一点,对于坐标平面内的定点N,定义
是l的一个法向量,M是l上一点,对于坐标平面内的定点N,定义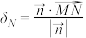 .用a、b、k、m表示
.用a、b、k、m表示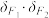 ,并利用
,并利用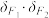 与
与 的大小关系,提出一个关于l与
的大小关系,提出一个关于l与 位置关系的真命题,给出该命题的证明.
位置关系的真命题,给出该命题的证明.
 的左、右焦点分别为
的左、右焦点分别为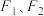 ,直线l的斜率为k,在y轴上的截距为m.
,直线l的斜率为k,在y轴上的截距为m.(1)设
 ,若
,若 的焦距为2,l过点
的焦距为2,l过点 ,求l的方程;
,求l的方程;(2)设
 ,若
,若 是
是 上的一点,且
上的一点,且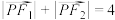 ,l与
,l与 交于不同的两点A、B,Q为
交于不同的两点A、B,Q为 的上顶点,求
的上顶点,求 面积的最大值;
面积的最大值;(3)设
 是l的一个法向量,M是l上一点,对于坐标平面内的定点N,定义
是l的一个法向量,M是l上一点,对于坐标平面内的定点N,定义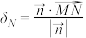 .用a、b、k、m表示
.用a、b、k、m表示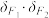 ,并利用
,并利用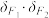 与
与 的大小关系,提出一个关于l与
的大小关系,提出一个关于l与 位置关系的真命题,给出该命题的证明.
位置关系的真命题,给出该命题的证明.
您最近一年使用:0次
2022-11-25更新
|
581次组卷
|
4卷引用:上海市虹口区2023届高三上学期11月适应性测试数学试题
上海市虹口区2023届高三上学期11月适应性测试数学试题上海海洋大学附属大团高级中学2023届高三上学期12月月考数学试题(已下线)高二下期中真题精选(易错46题专练)-【满分全攻略】2022-2023学年高二数学下学期核心考点+重难点讲练与测试(沪教版2020选修一+选修二)(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大题型)(练习)
名校
解题方法
10 . 已知椭圆 过点
过点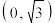 ,且离心率为
,且离心率为 .设
.设 ,
, 为椭圆
为椭圆 的左、右顶点,
的左、右顶点, 为椭圆上异于
为椭圆上异于 ,
, 的一点,直线
的一点,直线 ,
, 分别与直线
分别与直线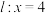 相交于
相交于 ,
, 两点,且直线
两点,且直线 与椭圆
与椭圆 交于另一点
交于另一点 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)求证:直线 与
与 的斜率之积为定值;
的斜率之积为定值;
(3)判断三点 ,
, ,
, 是否共线:并证明你的结论.
是否共线:并证明你的结论.
 过点
过点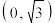 ,且离心率为
,且离心率为 .设
.设 ,
, 为椭圆
为椭圆 的左、右顶点,
的左、右顶点, 为椭圆上异于
为椭圆上异于 ,
, 的一点,直线
的一点,直线 ,
, 分别与直线
分别与直线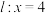 相交于
相交于 ,
, 两点,且直线
两点,且直线 与椭圆
与椭圆 交于另一点
交于另一点 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)求证:直线
 与
与 的斜率之积为定值;
的斜率之积为定值;(3)判断三点
 ,
, ,
, 是否共线:并证明你的结论.
是否共线:并证明你的结论.
您最近一年使用:0次
2022-10-11更新
|
1648次组卷
|
9卷引用:上海市2022届高三上学期一模暨春考模拟卷(五)数学试题



