解题方法
1 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,且经过点
,且经过点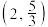 .
.
(1)求 的方程;
的方程;
(2)过 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线 交
交 于
于 两点,点
两点,点 为
为 的中点,记
的中点,记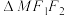 的面积为
的面积为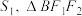 的面积为
的面积为 ,求
,求 的取值范围.
的取值范围.
 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,且经过点
,且经过点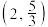 .
.(1)求
 的方程;
的方程;(2)过
 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线 交
交 于
于 两点,点
两点,点 为
为 的中点,记
的中点,记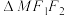 的面积为
的面积为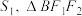 的面积为
的面积为 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
2 . 已知椭圆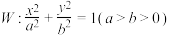 的离心率为
的离心率为 ,且过点
,且过点 .
.
(1)求 的方程;
的方程;
(2)直线 交
交 于
于 两点.
两点.
(i)点 关于原点的对称点为
关于原点的对称点为 ,直线
,直线 的斜率为
的斜率为 ,证明:
,证明: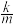 为定值;
为定值;
(ii)若 上存在点
上存在点 使得
使得 在
在 上的投影向量相等,且
上的投影向量相等,且 的重心在
的重心在 轴上,求直线
轴上,求直线 的方程.
的方程.
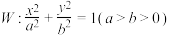 的离心率为
的离心率为 ,且过点
,且过点 .
.(1)求
 的方程;
的方程;(2)直线
 交
交 于
于 两点.
两点.(i)点
 关于原点的对称点为
关于原点的对称点为 ,直线
,直线 的斜率为
的斜率为 ,证明:
,证明: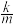 为定值;
为定值;(ii)若
 上存在点
上存在点 使得
使得 在
在 上的投影向量相等,且
上的投影向量相等,且 的重心在
的重心在 轴上,求直线
轴上,求直线 的方程.
的方程.
您最近一年使用:0次
2024-09-16更新
|
709次组卷
|
2卷引用:福建省福州市2024-2025学年高三上学期第一次质量检测数学试题
名校
解题方法
3 . 已知椭圆C: 的焦距为
的焦距为 ,离心率为
,离心率为 .
.
(1)求C的标准方程;
(2)若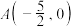 ,直线l:
,直线l: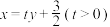 交椭圆C于E,F两点,且
交椭圆C于E,F两点,且 的面积为
的面积为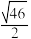 ,求t的值.
,求t的值.
 的焦距为
的焦距为 ,离心率为
,离心率为 .
.(1)求C的标准方程;
(2)若
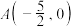 ,直线l:
,直线l: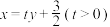 交椭圆C于E,F两点,且
交椭圆C于E,F两点,且 的面积为
的面积为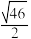 ,求t的值.
,求t的值.
您最近一年使用:0次
2024-09-03更新
|
2469次组卷
|
6卷引用:福建省厦门集美中学2025届高三上学期十月月考数学试卷
名校
解题方法
4 . 椭圆 的左、右焦点分别为
的左、右焦点分别为 为椭圆上第一象限内的一点,且
为椭圆上第一象限内的一点,且 与
与 轴相交于点
轴相交于点 ,离心率
,离心率 ,若
,若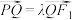 ,则
,则 ( )
( )
 的左、右焦点分别为
的左、右焦点分别为 为椭圆上第一象限内的一点,且
为椭圆上第一象限内的一点,且 与
与 轴相交于点
轴相交于点 ,离心率
,离心率 ,若
,若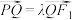 ,则
,则 ( )
( )A. | B. | C. | D. |
您最近一年使用:0次
名校
5 . 若椭圆 的离心率为
的离心率为 ,则该椭圆的焦距为( )
,则该椭圆的焦距为( )
 的离心率为
的离心率为 ,则该椭圆的焦距为( )
,则该椭圆的焦距为( )A. | B. | C. 或 或 | D. 或 或 |
您最近一年使用:0次
2024-06-09更新
|
802次组卷
|
3卷引用:福建省泉州第五中学2024届高三下学期适应性监测(二)数学试题
福建省泉州第五中学2024届高三下学期适应性监测(二)数学试题福建省福州第二中学2023-2024学年高二下学期期末测试数学试卷(已下线)第14讲 椭圆及其方程-【暑假自学课】(人教B版2019选择性必修第一册)
名校
解题方法
6 . 已知椭圆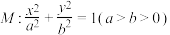 的离心率为
的离心率为 ,A,B,C分别为椭圆的左顶点,上顶点和右顶点,
,A,B,C分别为椭圆的左顶点,上顶点和右顶点, 为左焦点,且
为左焦点,且 的面积为
的面积为 .若P是椭圆M上不与顶点重合的动点,直线AB与直线CP交于点Q,直线BP交x轴于点N.
.若P是椭圆M上不与顶点重合的动点,直线AB与直线CP交于点Q,直线BP交x轴于点N.
(1)求椭圆M的标准方程;
(2)求证: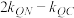 为定值,并求出此定值(其中
为定值,并求出此定值(其中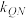 、
、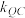 分别为直线QN和直线QC的斜率).
分别为直线QN和直线QC的斜率).
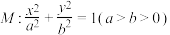 的离心率为
的离心率为 ,A,B,C分别为椭圆的左顶点,上顶点和右顶点,
,A,B,C分别为椭圆的左顶点,上顶点和右顶点, 为左焦点,且
为左焦点,且 的面积为
的面积为 .若P是椭圆M上不与顶点重合的动点,直线AB与直线CP交于点Q,直线BP交x轴于点N.
.若P是椭圆M上不与顶点重合的动点,直线AB与直线CP交于点Q,直线BP交x轴于点N.(1)求椭圆M的标准方程;
(2)求证:
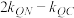 为定值,并求出此定值(其中
为定值,并求出此定值(其中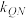 、
、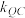 分别为直线QN和直线QC的斜率).
分别为直线QN和直线QC的斜率).
您最近一年使用:0次
名校
解题方法
7 . 已知椭圆 :
: 的离心率为
的离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,
, ,焦距为2,点
,焦距为2,点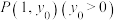 为椭圆
为椭圆 上的点.
上的点.
(1)求椭圆 的方程;
的方程;
(2)设点A,B在椭圆 上,直线PA,PB均与圆
上,直线PA,PB均与圆 :
: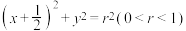 相切,证明:直线AB过定点.
相切,证明:直线AB过定点.
 :
: 的离心率为
的离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,
, ,焦距为2,点
,焦距为2,点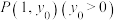 为椭圆
为椭圆 上的点.
上的点.(1)求椭圆
 的方程;
的方程;(2)设点A,B在椭圆
 上,直线PA,PB均与圆
上,直线PA,PB均与圆 :
: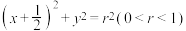 相切,证明:直线AB过定点.
相切,证明:直线AB过定点.
您最近一年使用:0次
名校
解题方法
8 . 已知椭圆 左、右顶点分别为
左、右顶点分别为 ,短轴长为
,短轴长为 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)若第一象限内一点 在椭圆上,且点
在椭圆上,且点 与
与 外接圆的圆心
外接圆的圆心 的连线交
的连线交 轴于点
轴于点 ,设
,设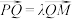 ,求实数
,求实数 的值.
的值.
 左、右顶点分别为
左、右顶点分别为 ,短轴长为
,短轴长为 ,离心率为
,离心率为 .
.(1)求椭圆
 的方程;
的方程;(2)若第一象限内一点
 在椭圆上,且点
在椭圆上,且点 与
与 外接圆的圆心
外接圆的圆心 的连线交
的连线交 轴于点
轴于点 ,设
,设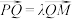 ,求实数
,求实数 的值.
的值.
您最近一年使用:0次
2024-05-23更新
|
410次组卷
|
2卷引用:福建省福州市联盟校2023-2024学年高二下学期期末考试数学试题
名校
9 . 一般地,我们把离心率为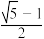 的椭圆称为“黄金椭圆”,则下列命题正确的有( )
的椭圆称为“黄金椭圆”,则下列命题正确的有( )
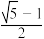 的椭圆称为“黄金椭圆”,则下列命题正确的有( )
的椭圆称为“黄金椭圆”,则下列命题正确的有( )A.椭圆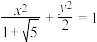 是“黄金椭圆” 是“黄金椭圆” |
B.若椭圆 是黄金椭圆,则 是黄金椭圆,则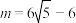 |
C.设“黄金椭圆”C的左右焦点分别为 ,存在椭圆C上一点P,使得 ,存在椭圆C上一点P,使得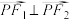 |
D.设过原点的直线与焦点在x轴上的“黄金椭圆”分别交于A、B两点,“黄金椭圆”上动点P(异于A,B),设直线PA,PB的斜率分别为 ,则 ,则 |
您最近一年使用:0次
2024-05-22更新
|
859次组卷
|
3卷引用:福建省宁德市博雅培文学校2024-2025学年高二上学期9月月考数学试卷
10 . 已知椭圆 的离心率为
的离心率为 ,点
,点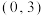 在
在 上.
上.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知动直线 过曲线
过曲线 的左焦点
的左焦点 ,且与椭圆
,且与椭圆 分别交于
分别交于 ,
, 两点,试问
两点,试问 轴上是否存在定点
轴上是否存在定点 ,使得
,使得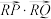 为定值?若存在,求出该定点坐标;若不存在,请说明理由.
为定值?若存在,求出该定点坐标;若不存在,请说明理由.
 的离心率为
的离心率为 ,点
,点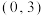 在
在 上.
上.(1)求椭圆
 的标准方程;
的标准方程;(2)已知动直线
 过曲线
过曲线 的左焦点
的左焦点 ,且与椭圆
,且与椭圆 分别交于
分别交于 ,
, 两点,试问
两点,试问 轴上是否存在定点
轴上是否存在定点 ,使得
,使得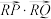 为定值?若存在,求出该定点坐标;若不存在,请说明理由.
为定值?若存在,求出该定点坐标;若不存在,请说明理由.
您最近一年使用:0次



