名校
解题方法
1 . 已知椭圆 的离心率为
的离心率为 ,椭圆的一个顶点与两个焦点构成的三角形面积为2. 已知直线
,椭圆的一个顶点与两个焦点构成的三角形面积为2. 已知直线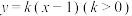 与椭圆C交于A,B两点,且与x轴,y轴交于M,N两点.
与椭圆C交于A,B两点,且与x轴,y轴交于M,N两点.
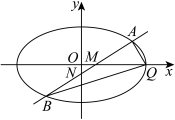
(1)求椭圆C的标准方程;
(2)若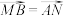 ,求k的值;
,求k的值;
(3)若点Q的坐标为 ,求证:
,求证: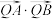 为定值.
为定值.
 的离心率为
的离心率为 ,椭圆的一个顶点与两个焦点构成的三角形面积为2. 已知直线
,椭圆的一个顶点与两个焦点构成的三角形面积为2. 已知直线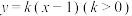 与椭圆C交于A,B两点,且与x轴,y轴交于M,N两点.
与椭圆C交于A,B两点,且与x轴,y轴交于M,N两点.
(1)求椭圆C的标准方程;
(2)若
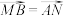 ,求k的值;
,求k的值;(3)若点Q的坐标为
 ,求证:
,求证: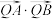 为定值.
为定值.
您最近一年使用:0次
2023-12-25更新
|
1460次组卷
|
10卷引用:【全国市级联考】天津市部分区2018年高三质量调查(二)数学(文)试题
【全国市级联考】天津市部分区2018年高三质量调查(二)数学(文)试题上海市嘉定区第二中学2023-2024学年高二下学期3月月考数学试题(已下线)专题44 盘点圆锥曲线中的定值问题——备战2022年高考数学二轮复习常考点专题突破上海交通大学附属中学2023届高三下学期期中数学试题(已下线)重难点突破16 圆锥曲线中的定点、定值问题 (十大题型)-1上海市浦东新区进才中学2023-2024学年高二上学期12月月考数学试题广东省广州市广东实验中学2024届高三上学期大湾区数学冲刺卷(一)宁夏银川市宁夏育才中学2023-2024学年高三上学期月考五数学(理科)试卷上海市新川中学2023-2024学年高二上学期期末数学试题广西壮族自治区百色市德保县德保高中2023-2024学年高二下学期3月月考数学试题
2 . 已知椭圆方程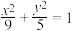 ,直线
,直线 与椭圆相交于
与椭圆相交于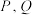 两点,O为坐标原点,是否存在实数k满足
两点,O为坐标原点,是否存在实数k满足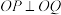 ,若不存在说明理由,若存在求出实数k的值.
,若不存在说明理由,若存在求出实数k的值.
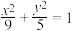 ,直线
,直线 与椭圆相交于
与椭圆相交于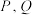 两点,O为坐标原点,是否存在实数k满足
两点,O为坐标原点,是否存在实数k满足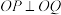 ,若不存在说明理由,若存在求出实数k的值.
,若不存在说明理由,若存在求出实数k的值.
您最近一年使用:0次
名校
解题方法
3 . 已知椭圆 :
: (
( )的左右焦点分别为
)的左右焦点分别为 ,
,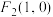 ,且椭圆上一点P,满足
,且椭圆上一点P,满足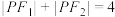 .
.
(1)求椭圆C的标准方程;
(2)设椭圆C的左顶点为A,若椭圆C上存在点Q,使得四边形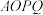 是平行四边形(其中O为坐标原点,点P在第一象限),求直线
是平行四边形(其中O为坐标原点,点P在第一象限),求直线 与
与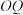 的斜率之积:
的斜率之积:
(3)记圆 为椭圆C的“关联圆”.过点P作椭圆C的“关联圆”的两条切线,切点为M、N,直线
为椭圆C的“关联圆”.过点P作椭圆C的“关联圆”的两条切线,切点为M、N,直线 的横、纵截距分别为m、n,求证:
的横、纵截距分别为m、n,求证: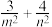 为定值.
为定值.
 :
: (
( )的左右焦点分别为
)的左右焦点分别为 ,
,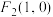 ,且椭圆上一点P,满足
,且椭圆上一点P,满足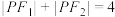 .
.(1)求椭圆C的标准方程;
(2)设椭圆C的左顶点为A,若椭圆C上存在点Q,使得四边形
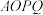 是平行四边形(其中O为坐标原点,点P在第一象限),求直线
是平行四边形(其中O为坐标原点,点P在第一象限),求直线 与
与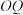 的斜率之积:
的斜率之积:(3)记圆
 为椭圆C的“关联圆”.过点P作椭圆C的“关联圆”的两条切线,切点为M、N,直线
为椭圆C的“关联圆”.过点P作椭圆C的“关联圆”的两条切线,切点为M、N,直线 的横、纵截距分别为m、n,求证:
的横、纵截距分别为m、n,求证: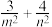 为定值.
为定值.
您最近一年使用:0次
4 . 如图,已知椭圆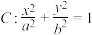
 过点
过点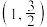 两个焦点为
两个焦点为 和
和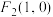 .圆O的方程为
.圆O的方程为 .
.

(1)求椭圆C的标准方程;
(2)过 且斜率为
且斜率为 的动直线l与椭圆C交于A、B两点,与圆O交于P、Q两点(点A、P在x轴上方),当
的动直线l与椭圆C交于A、B两点,与圆O交于P、Q两点(点A、P在x轴上方),当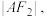
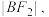
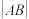 成等差数列时,求弦PQ的长.
成等差数列时,求弦PQ的长.
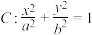
 过点
过点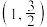 两个焦点为
两个焦点为 和
和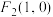 .圆O的方程为
.圆O的方程为 .
.
(1)求椭圆C的标准方程;
(2)过
 且斜率为
且斜率为 的动直线l与椭圆C交于A、B两点,与圆O交于P、Q两点(点A、P在x轴上方),当
的动直线l与椭圆C交于A、B两点,与圆O交于P、Q两点(点A、P在x轴上方),当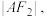
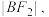
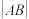 成等差数列时,求弦PQ的长.
成等差数列时,求弦PQ的长.
您最近一年使用:0次
5 . 如图,已知椭圆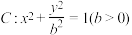 ,直线
,直线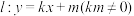 ,直线
,直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,点
,点 和点
和点 关于
关于 轴对称,直线
轴对称,直线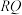 与
与 轴交于点
轴交于点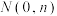 .
.
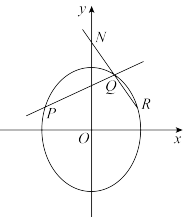
(1)若点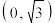 是椭圆
是椭圆 的一个焦点,求该椭圆的长轴的长度;
的一个焦点,求该椭圆的长轴的长度;
(2)若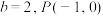 ,且
,且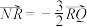 ,求
,求 的值;
的值;
(3)若 ,求证:
,求证: 为定值.
为定值.
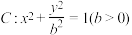 ,直线
,直线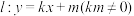 ,直线
,直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,点
,点 和点
和点 关于
关于 轴对称,直线
轴对称,直线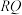 与
与 轴交于点
轴交于点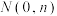 .
.
(1)若点
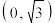 是椭圆
是椭圆 的一个焦点,求该椭圆的长轴的长度;
的一个焦点,求该椭圆的长轴的长度;(2)若
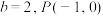 ,且
,且 ,求
,求 的值;
的值;(3)若
 ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
6 . 已知椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 的直线
的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点.
两点.
(1)求 的周长;
的周长;
(2)设点 为椭圆
为椭圆 的上顶点,点
的上顶点,点 在第一象限,点
在第一象限,点 在线段
在线段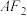 上.若
上.若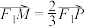 ,求点
,求点 的横坐标;
的横坐标;
(3)设直线 不平行于坐标轴,点
不平行于坐标轴,点 为点
为点 关于
关于 轴的对称点,直线
轴的对称点,直线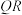 与
与 轴交于点
轴交于点 .求
.求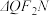 面积的最大值.
面积的最大值.
 :
: 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 的直线
的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点.
两点.(1)求
 的周长;
的周长;(2)设点
 为椭圆
为椭圆 的上顶点,点
的上顶点,点 在第一象限,点
在第一象限,点 在线段
在线段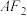 上.若
上.若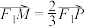 ,求点
,求点 的横坐标;
的横坐标;(3)设直线
 不平行于坐标轴,点
不平行于坐标轴,点 为点
为点 关于
关于 轴的对称点,直线
轴的对称点,直线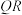 与
与 轴交于点
轴交于点 .求
.求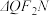 面积的最大值.
面积的最大值.
您最近一年使用:0次
2019-04-28更新
|
514次组卷
|
3卷引用:上海市嘉定(长宁)区2019届高三第二次质量调研(二模)数学试题
名校
7 . 已知椭圆 :
: 的长轴长为
的长轴长为 ,右顶点到左焦点的距离为
,右顶点到左焦点的距离为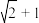 ,直线l:
,直线l: 与椭圆
与椭圆 交于A,B两点.
交于A,B两点. 求椭圆
求椭圆 的方程;
的方程;
 若A为椭圆的上顶点,M为AB中点,O为坐标原点,连接OM并延长交椭圆
若A为椭圆的上顶点,M为AB中点,O为坐标原点,连接OM并延长交椭圆 于N,
于N,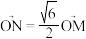 ,求k的值.
,求k的值.
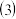 若原点O到直线l的距离为1,
若原点O到直线l的距离为1,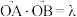 ,当
,当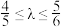 时,求
时,求 的面积S的范围.
的面积S的范围.
 :
: 的长轴长为
的长轴长为 ,右顶点到左焦点的距离为
,右顶点到左焦点的距离为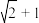 ,直线l:
,直线l: 与椭圆
与椭圆 交于A,B两点.
交于A,B两点.
 求椭圆
求椭圆 的方程;
的方程; 若A为椭圆的上顶点,M为AB中点,O为坐标原点,连接OM并延长交椭圆
若A为椭圆的上顶点,M为AB中点,O为坐标原点,连接OM并延长交椭圆 于N,
于N,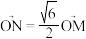 ,求k的值.
,求k的值.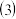 若原点O到直线l的距离为1,
若原点O到直线l的距离为1,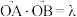 ,当
,当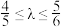 时,求
时,求 的面积S的范围.
的面积S的范围.
您最近一年使用:0次
2019-03-28更新
|
236次组卷
|
4卷引用:上海市嘉定区第一中学2020-2021学年高二上学期12月月考数学试题
名校
8 . 如图, 是椭圆
是椭圆 长轴的两个端点,
长轴的两个端点, 是椭圆上与
是椭圆上与 均不重合的相异两点,设直线
均不重合的相异两点,设直线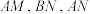 的斜率分别是
的斜率分别是 .
.
(1)求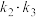 的值;
的值;
(2)若直线 过点
过点 ,求证:
,求证: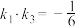 ;
;
(3)设直线 与
与 轴的交点为
轴的交点为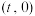 (
( 为常数且
为常数且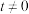 ),试探究直线
),试探究直线 与直线
与直线 的交点
的交点 是否落在某条定直线上?若是,请求出该定直线的方程;若不是,请说明理由.
是否落在某条定直线上?若是,请求出该定直线的方程;若不是,请说明理由.
 是椭圆
是椭圆 长轴的两个端点,
长轴的两个端点, 是椭圆上与
是椭圆上与 均不重合的相异两点,设直线
均不重合的相异两点,设直线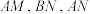 的斜率分别是
的斜率分别是 .
.(1)求
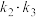 的值;
的值;(2)若直线
 过点
过点 ,求证:
,求证: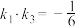 ;
;(3)设直线
 与
与 轴的交点为
轴的交点为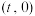 (
( 为常数且
为常数且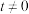 ),试探究直线
),试探究直线 与直线
与直线 的交点
的交点 是否落在某条定直线上?若是,请求出该定直线的方程;若不是,请说明理由.
是否落在某条定直线上?若是,请求出该定直线的方程;若不是,请说明理由.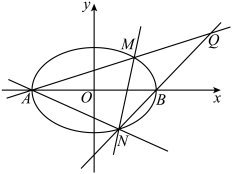
您最近一年使用:0次
2018-04-15更新
|
1833次组卷
|
8卷引用:【区级联考】上海市徐汇区2018届高三下学期学习能力诊断(二模)数学试题
【区级联考】上海市徐汇区2018届高三下学期学习能力诊断(二模)数学试题上海市育才中学2023届高三上学期期中数学试题上海市建平中学2020-2021学年高二下学期3月月考数学试题(已下线)专题24 圆锥曲线中的存在性、探索性问题 微点2 圆锥曲线中的探索性问题上海市五校2022-2023学年高二下学期3月联考数学试题(已下线)第2章 圆锥曲线(基础、常考、易错、压轴)分类专项训练(2)(已下线)高二下期中真题精选(常考60题专练)-【满分全攻略】2022-2023学年高二数学下学期核心考点+重难点讲练与测试(沪教版2020选修一+选修二)(已下线)专题3 曲线系方程及其应用【讲】(压轴题大全)
2013·上海黄浦·二模
名校
9 . 如果函数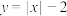 的图像与曲线
的图像与曲线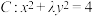 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数 的取值范围是
的取值范围是
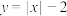 的图像与曲线
的图像与曲线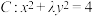 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数 的取值范围是
的取值范围是A.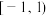 | B. | C.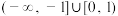 | D. |
您最近一年使用:0次
2016-12-02更新
|
1430次组卷
|
4卷引用:上海市嘉定区第二中学2020-2021学年高二上学期第二次月考数学试题
上海市嘉定区第二中学2020-2021学年高二上学期第二次月考数学试题(已下线)2013届上海市黄浦区高三下学期二模数学试卷2016届上海市南洋模范中学高三5月三模数学试题上海市进才中学2023-2024学年高二下学期3月月考数学试题



