名校
解题方法
1 . 在平面直角坐标系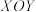 中, 已知两定点
中, 已知两定点 , 点
, 点 满足
满足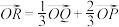 且在焦点在
且在焦点在 轴正半轴的抛物线
轴正半轴的抛物线 上. 过
上. 过 作一斜率存在的直线交
作一斜率存在的直线交 于
于 两点, 连接
两点, 连接 交抛物线
交抛物线 于点
于点 .
.
(1)求抛物线 的标准方程;
的标准方程;
(2)判断直线 是否恒过定点,若是请求出该定点坐标,若不是请说明理由.
是否恒过定点,若是请求出该定点坐标,若不是请说明理由.
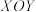 中, 已知两定点
中, 已知两定点 , 点
, 点 满足
满足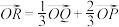 且在焦点在
且在焦点在 轴正半轴的抛物线
轴正半轴的抛物线 上. 过
上. 过 作一斜率存在的直线交
作一斜率存在的直线交 于
于 两点, 连接
两点, 连接 交抛物线
交抛物线 于点
于点 .
.(1)求抛物线
 的标准方程;
的标准方程;(2)判断直线
 是否恒过定点,若是请求出该定点坐标,若不是请说明理由.
是否恒过定点,若是请求出该定点坐标,若不是请说明理由.
您最近一年使用:0次
名校
2 . 抛物线 :
: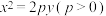 焦点为
焦点为 ,且过点
,且过点 ,直线
,直线 ,
, 分别交
分别交 于另一点C和D,
于另一点C和D, ,则下列说法正确的是( )
,则下列说法正确的是( )
 :
: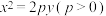 焦点为
焦点为 ,且过点
,且过点 ,直线
,直线 ,
, 分别交
分别交 于另一点C和D,
于另一点C和D, ,则下列说法正确的是( )
,则下列说法正确的是( )A. |
B.直线 过定点 过定点 |
C. 上任意一点到点 上任意一点到点 和直线 和直线 的距离相等 的距离相等 |
D. |
您最近一年使用:0次
2023-11-23更新
|
444次组卷
|
3卷引用:3.3.1 抛物线及其标准方程(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)
(已下线)3.3.1 抛物线及其标准方程(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)河南省开封市五县2023-2024学年高二上学期期中联考数学试题广东省汕尾市华南师范大学附属中学汕尾学校2024届高三下学期3月月考数学试题
3 . 设抛物线 :
: 的焦点为F,经过x轴正半轴上点
的焦点为F,经过x轴正半轴上点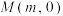 的直线l交
的直线l交 于不同的两点A和B.
于不同的两点A和B.

(1)若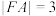 ,求A点的坐标;
,求A点的坐标;
(2)若 ,求
,求 的值;
的值;
(3)若 ,且直线
,且直线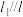 ,
, 与
与 有且只有一个公共点E,问:
有且只有一个公共点E,问: 的面积是否存在最小值?若存在,求出最小值,并求出M点的坐标;若不存在,请说明理由(三角形面积公式:在
的面积是否存在最小值?若存在,求出最小值,并求出M点的坐标;若不存在,请说明理由(三角形面积公式:在 中,设
中,设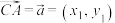 ,
, ,则
,则 的面积为
的面积为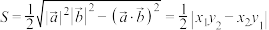 ).
).
 :
: 的焦点为F,经过x轴正半轴上点
的焦点为F,经过x轴正半轴上点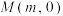 的直线l交
的直线l交 于不同的两点A和B.
于不同的两点A和B.
(1)若
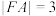 ,求A点的坐标;
,求A点的坐标;(2)若
 ,求
,求 的值;
的值;(3)若
 ,且直线
,且直线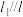 ,
, 与
与 有且只有一个公共点E,问:
有且只有一个公共点E,问: 的面积是否存在最小值?若存在,求出最小值,并求出M点的坐标;若不存在,请说明理由(三角形面积公式:在
的面积是否存在最小值?若存在,求出最小值,并求出M点的坐标;若不存在,请说明理由(三角形面积公式:在 中,设
中,设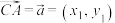 ,
, ,则
,则 的面积为
的面积为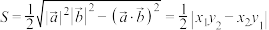 ).
).
您最近一年使用:0次
解题方法
4 . 已知 为坐标原点,
为坐标原点,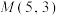 ,点
,点 、
、 是抛物线
是抛物线 上两点,
上两点, 为
为 的焦点,则下列说法正确的有( )
的焦点,则下列说法正确的有( )
 为坐标原点,
为坐标原点,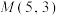 ,点
,点 、
、 是抛物线
是抛物线 上两点,
上两点, 为
为 的焦点,则下列说法正确的有( )
的焦点,则下列说法正确的有( )A.若 ,则 ,则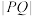 最小值为 最小值为 | B.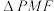 周长的最小值为 周长的最小值为 |
C. 为直径的圆与 为直径的圆与 轴相切 轴相切 | D.若直线 经过点 经过点 ,则 ,则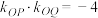 |
您最近一年使用:0次
名校
解题方法
5 . 已知抛物线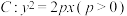 经过点
经过点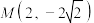 ,直线
,直线 与抛物线相交于不同的
与抛物线相交于不同的 、
、 两点.
两点.
(1)求抛物线 的方程;
的方程;
(2)如果 ,直线
,直线 是否过一定点,若过一定点,求出该定点;若不过一定点,试说明理由.
是否过一定点,若过一定点,求出该定点;若不过一定点,试说明理由.
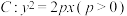 经过点
经过点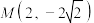 ,直线
,直线 与抛物线相交于不同的
与抛物线相交于不同的 、
、 两点.
两点.(1)求抛物线
 的方程;
的方程;(2)如果
 ,直线
,直线 是否过一定点,若过一定点,求出该定点;若不过一定点,试说明理由.
是否过一定点,若过一定点,求出该定点;若不过一定点,试说明理由.
您最近一年使用:0次
2023-11-11更新
|
1483次组卷
|
5卷引用:3.3.1 抛物线及其标准方程(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)
(已下线)3.3.1 抛物线及其标准方程(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)辽宁省沈阳市第二中学2023-2024学年高二上学期第二次月考数学试题山东省临沂市第十九中学2023-2024学年高二上学期第五次质量调研考试数学试题湖南省湖湘教育三新探索协作体2023-2024学年高二上学期11月期中联考数学试题吉林省通化市梅河口市第五中学2023-2024学年高二上学期第三次月考数学试题
2023高三·全国·专题练习
6 . 设抛物线E: 的焦点为F,点A,B是抛物线E上不同的两点,且
的焦点为F,点A,B是抛物线E上不同的两点,且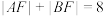 ,则( )
,则( )
 的焦点为F,点A,B是抛物线E上不同的两点,且
的焦点为F,点A,B是抛物线E上不同的两点,且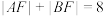 ,则( )
,则( )| A.线段AB的中点到E的准线的距离为4 |
B.直线AB过原点时, |
C.直线AB的倾斜角的取值范围为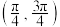 |
| D.线段AB的垂直平分线过某一定点 |
您最近一年使用:0次
7 . 在平面直角坐标系 中,已知圆心为
中,已知圆心为 的动圆过点
的动圆过点 ,且在
,且在 轴上截得的弦长为4,记
轴上截得的弦长为4,记 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线
 的方程;
的方程;(2)已知
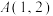 及曲线
及曲线 上的两点
上的两点 和
和 ,直线
,直线 经过定点
经过定点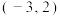 ,直线
,直线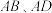 的斜率分别为
的斜率分别为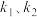 ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
2023-10-18更新
|
837次组卷
|
3卷引用:3.3.2 抛物线的简单几何性质(6大题型)精练-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)
(已下线)3.3.2 抛物线的简单几何性质(6大题型)精练-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)江苏省南京外国语学校2023-2024学年高二上学期10月月考数学试题(已下线)专题26 直线与圆锥曲线的位置关系5种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教B版2019选择性必修第一册)
8 . 已知椭圆 :
: 的离心率为
的离心率为 ,
, 的左右焦点分别为
的左右焦点分别为 ,
, ,
, 是椭圆上任意一点,满足
是椭圆上任意一点,满足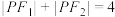 .抛物线
.抛物线 :
: 的焦点
的焦点 与椭圆
与椭圆 的右焦点
的右焦点 重合,点
重合,点 是抛物线
是抛物线 的准线上任意一点,直线
的准线上任意一点,直线 ,
, 分别与抛物线
分别与抛物线 相切于点
相切于点 .
.
(1)若直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,且
两点,且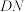 的中点为
的中点为 ,求直线
,求直线 的方程;
的方程;
(2)设直线 ,
, 的斜率分别为
的斜率分别为 ,
, ,证明:
,证明: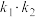 为定值.
为定值.
 :
: 的离心率为
的离心率为 ,
, 的左右焦点分别为
的左右焦点分别为 ,
, ,
, 是椭圆上任意一点,满足
是椭圆上任意一点,满足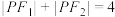 .抛物线
.抛物线 :
: 的焦点
的焦点 与椭圆
与椭圆 的右焦点
的右焦点 重合,点
重合,点 是抛物线
是抛物线 的准线上任意一点,直线
的准线上任意一点,直线 ,
, 分别与抛物线
分别与抛物线 相切于点
相切于点 .
.(1)若直线
 与椭圆
与椭圆 相交于
相交于 ,
, 两点,且
两点,且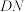 的中点为
的中点为 ,求直线
,求直线 的方程;
的方程;(2)设直线
 ,
, 的斜率分别为
的斜率分别为 ,
, ,证明:
,证明: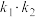 为定值.
为定值.
您最近一年使用:0次
2023-10-13更新
|
1114次组卷
|
7卷引用:3.3.2 抛物线的简单的几何性质(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)
(已下线)3.3.2 抛物线的简单的几何性质(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)江西省上饶市广丰中学2023-2024学年高二上学期10月月考数学试题(已下线)考点16 解析几何中的定值问题 2024届高考数学考点总动员(已下线)专题08 抛物线的压轴题(5类题型+过关检测)-【常考压轴题】2023-2024学年高二数学上学期压轴题攻略(人教A版2019选择性必修第一册)(已下线)专题27 抛物线的简单几何性质7种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)云南省曲靖市第一中学2024届高三上学期第二次月考数学试题河北省石家庄市第二中学2023-2024学年高二上学期期末模拟一数学试题
9 . 设O为坐标原点,点M,N在抛物线 上,且
上,且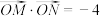 .
.
(1)证明:直线 过定点;
过定点;
(2)设C在点M,N处的切线相交于点P,求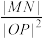 的取值范围.
的取值范围.
 上,且
上,且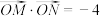 .
.(1)证明:直线
 过定点;
过定点;(2)设C在点M,N处的切线相交于点P,求
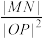 的取值范围.
的取值范围.
您最近一年使用:0次
10 . 直线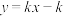 过抛物线
过抛物线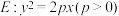 的焦点且与该抛物线交于M,N两点,设O为坐标原点,则下列说法中正确的是( )
的焦点且与该抛物线交于M,N两点,设O为坐标原点,则下列说法中正确的是( )
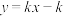 过抛物线
过抛物线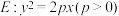 的焦点且与该抛物线交于M,N两点,设O为坐标原点,则下列说法中正确的是( )
的焦点且与该抛物线交于M,N两点,设O为坐标原点,则下列说法中正确的是( )A. | B.抛物线E的准线方程是 |
| C.以MN为直径的圆与定直线相切 | D.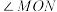 的大小为定值 的大小为定值 |
您最近一年使用:0次
2023-09-05更新
|
1421次组卷
|
6卷引用:重难点03: 直线与抛物线的位置关系(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)
(已下线)重难点03: 直线与抛物线的位置关系(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)湖北省武汉市部分学校2023-2024学年高三上学期九月调研考试数学试题江苏省南京市第九中学2023-2024学年高二上学期10月阶段学情调研数学试题(已下线)模块三 专题5 圆锥曲线中的定值和定点问题(高二人教A)(已下线)专题27 抛物线的简单几何性质7种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)云南省长水教育集团2024届高三上学期10月质量检测数学试题



