名校
解题方法
1 . 已知椭圆 :
: 的右焦点F在直线
的右焦点F在直线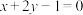 上,A,B分别为
上,A,B分别为 的左、右顶点,且
的左、右顶点,且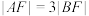 .
.
(1)求C的标准方程;
(2)是否存在过点 的直线
的直线 交C于M,N两点,使得直线
交C于M,N两点,使得直线 ,
, 的斜率之和等于-1?若存在,求出
的斜率之和等于-1?若存在,求出 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 :
: 的右焦点F在直线
的右焦点F在直线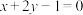 上,A,B分别为
上,A,B分别为 的左、右顶点,且
的左、右顶点,且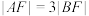 .
.(1)求C的标准方程;
(2)是否存在过点
 的直线
的直线 交C于M,N两点,使得直线
交C于M,N两点,使得直线 ,
, 的斜率之和等于-1?若存在,求出
的斜率之和等于-1?若存在,求出 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
您最近一年使用:0次
2024-11-02更新
|
1110次组卷
|
2卷引用:福建省福州第三中学2024-2025学年高三上学期10月月考数学试题
名校
解题方法
2 . 已知椭圆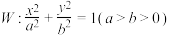 的离心率为
的离心率为 ,且过点
,且过点 .
.
(1)求 的方程;
的方程;
(2)直线 交
交 于
于 两点.
两点.
(i)点 关于原点的对称点为
关于原点的对称点为 ,直线
,直线 的斜率为
的斜率为 ,证明:
,证明: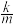 为定值;
为定值;
(ii)若 上存在点
上存在点 使得
使得 在
在 上的投影向量相等,且
上的投影向量相等,且 的重心在
的重心在 轴上,求直线
轴上,求直线 的方程.
的方程.
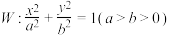 的离心率为
的离心率为 ,且过点
,且过点 .
.(1)求
 的方程;
的方程;(2)直线
 交
交 于
于 两点.
两点.(i)点
 关于原点的对称点为
关于原点的对称点为 ,直线
,直线 的斜率为
的斜率为 ,证明:
,证明: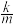 为定值;
为定值;(ii)若
 上存在点
上存在点 使得
使得 在
在 上的投影向量相等,且
上的投影向量相等,且 的重心在
的重心在 轴上,求直线
轴上,求直线 的方程.
的方程.
您最近一年使用:0次
2024-09-16更新
|
765次组卷
|
2卷引用:福建省福州市2024-2025学年高三上学期第一次质量检测数学试题
名校
解题方法
3 . 已知 是椭圆
是椭圆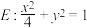 的左,右顶点,点
的左,右顶点,点 与椭圆上的点的距离的最小值为1.
与椭圆上的点的距离的最小值为1.
(1)求点 的坐标.
的坐标.
(2)过点 作直线
作直线 交椭圆
交椭圆 于
于 两点(与
两点(与 不重合),连接
不重合),连接 ,
, 交于点
交于点 .
.
(ⅰ)证明:点 在定直线上;
在定直线上;
(ⅱ)是否存在点 使得
使得 ,若存在,求出直线
,若存在,求出直线 的斜率;若不存在,请说明理由.
的斜率;若不存在,请说明理由.
 是椭圆
是椭圆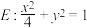 的左,右顶点,点
的左,右顶点,点 与椭圆上的点的距离的最小值为1.
与椭圆上的点的距离的最小值为1.(1)求点
 的坐标.
的坐标.(2)过点
 作直线
作直线 交椭圆
交椭圆 于
于 两点(与
两点(与 不重合),连接
不重合),连接 ,
, 交于点
交于点 .
.(ⅰ)证明:点
 在定直线上;
在定直线上;(ⅱ)是否存在点
 使得
使得 ,若存在,求出直线
,若存在,求出直线 的斜率;若不存在,请说明理由.
的斜率;若不存在,请说明理由.
您最近一年使用:0次
2024-04-16更新
|
3142次组卷
|
6卷引用:福建省龙岩市2024届高三适应性练习(三)数学试题
名校
解题方法
4 . 已知椭圆 :
: 的离心率为
的离心率为 ,A,B分别是E的左、右顶点,P是E上异于A,B的点,
,A,B分别是E的左、右顶点,P是E上异于A,B的点,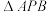 的面积的最大值为
的面积的最大值为 .
.
(1)求E的方程;
(2)设O为原点,点N在直线 上,N,P分别在x轴的两侧,且
上,N,P分别在x轴的两侧,且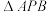 与
与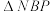 的面积相等.
的面积相等.
(i)求证:直线 与直线
与直线 的斜率之积为定值;
的斜率之积为定值;
(ⅱ)是否存在点P使得 ,若存在,求出点P的坐标,若不存在,说明理由.
,若存在,求出点P的坐标,若不存在,说明理由.
 :
: 的离心率为
的离心率为 ,A,B分别是E的左、右顶点,P是E上异于A,B的点,
,A,B分别是E的左、右顶点,P是E上异于A,B的点,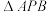 的面积的最大值为
的面积的最大值为 .
.(1)求E的方程;
(2)设O为原点,点N在直线
 上,N,P分别在x轴的两侧,且
上,N,P分别在x轴的两侧,且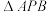 与
与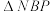 的面积相等.
的面积相等.(i)求证:直线
 与直线
与直线 的斜率之积为定值;
的斜率之积为定值;(ⅱ)是否存在点P使得
 ,若存在,求出点P的坐标,若不存在,说明理由.
,若存在,求出点P的坐标,若不存在,说明理由.
您最近一年使用:0次
2024-04-09更新
|
1434次组卷
|
4卷引用:福建省厦门第一中学2024-2025学年高三上学期入学考试数学试卷
福建省厦门第一中学2024-2025学年高三上学期入学考试数学试卷北京市朝阳区2024届高三下学期质量检测一数学试题北京市大峪中学2025届高三上学期开学定位考试数学试题(已下线)周测18 圆锥曲线(一轮好卷北京专版 )
名校
解题方法
5 . 在平面直角坐标系 中,椭圆
中,椭圆 的左,右顶点分别为
的左,右顶点分别为 、
、 ,点
,点 是椭圆的右焦点,
是椭圆的右焦点,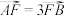 ,
,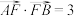 .
.
(1)求椭圆 的方程;
的方程;
(2)经过椭圆右焦点 且斜率不为零的动直线
且斜率不为零的动直线 与椭圆交于
与椭圆交于 、
、 两点,试问
两点,试问 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点 ,使
,使 恒成立?若存在,求出
恒成立?若存在,求出 点坐标,若不存在,说明理由.
点坐标,若不存在,说明理由.
 中,椭圆
中,椭圆 的左,右顶点分别为
的左,右顶点分别为 、
、 ,点
,点 是椭圆的右焦点,
是椭圆的右焦点,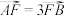 ,
,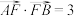 .
.(1)求椭圆
 的方程;
的方程;(2)经过椭圆右焦点
 且斜率不为零的动直线
且斜率不为零的动直线 与椭圆交于
与椭圆交于 、
、 两点,试问
两点,试问 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点 ,使
,使 恒成立?若存在,求出
恒成立?若存在,求出 点坐标,若不存在,说明理由.
点坐标,若不存在,说明理由.
您最近一年使用:0次
2023-12-31更新
|
1218次组卷
|
6卷引用:福建省福州格致中学2023-2024学年高二下学期3月限时训练(月考)数学试卷
福建省福州格致中学2023-2024学年高二下学期3月限时训练(月考)数学试卷宁夏银川市银川一中2024届高三上学期第五次月考数学(文)试题江苏省苏州市南航苏州附中2024届高三上学期零模模拟数学试题(已下线)专题18 圆锥曲线高频压轴解答题(16大题型)(练习)广东省深圳市福田区福田中学2024届高三下学期开学考试数学试题(已下线)黄金卷08
6 . 已知 为坐标原点,椭圆
为坐标原点,椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
,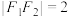 ,
, 为椭圆的上顶点,以
为椭圆的上顶点,以 为圆心且过
为圆心且过 ,
, 的圆与直线
的圆与直线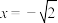 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)已知直线 与椭圆
与椭圆 交于
交于 ,
, 两点,若
两点,若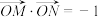 ,点
,点 在
在 上,
上, .证明:存在点
.证明:存在点 ,使得
,使得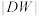 为定值.
为定值.
 为坐标原点,椭圆
为坐标原点,椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
,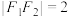 ,
, 为椭圆的上顶点,以
为椭圆的上顶点,以 为圆心且过
为圆心且过 ,
, 的圆与直线
的圆与直线 相切.
相切.(1)求椭圆
 的方程;
的方程;(2)已知直线
 与椭圆
与椭圆 交于
交于 ,
, 两点,若
两点,若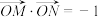 ,点
,点 在
在 上,
上, .证明:存在点
.证明:存在点 ,使得
,使得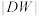 为定值.
为定值.
您最近一年使用:0次
名校
解题方法
7 . 椭圆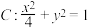 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
, 为坐标原点,则以下说法正确的是( )
为坐标原点,则以下说法正确的是( )
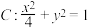 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
, 为坐标原点,则以下说法正确的是( )
为坐标原点,则以下说法正确的是( )A.过点 的直线与椭圆 的直线与椭圆 交于 交于 , , 两点,则 两点,则 的周长为8 的周长为8 |
B.椭圆 上存在点 上存在点 ,使得 ,使得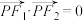 |
C.椭圆 的离心率为 的离心率为 |
D. 为椭圆 为椭圆 上一点, 上一点, 为圆 为圆 上一点,则点 上一点,则点 , , 的最大距离为3 的最大距离为3 |
您最近一年使用:0次
2021-09-08更新
|
1998次组卷
|
27卷引用:福建省三明市三明第一中学2019-2020学年高二上学期12月月考数学试题
福建省三明市三明第一中学2019-2020学年高二上学期12月月考数学试题厦门市国祺中学2020-2021学年高二上数学第一次月考试题福建省厦门市湖滨中学2020-2021学年高二上学期期中考试数学试题福建省福州民族中学2020-2021学年高二10月月考数学试题福建省厦门大学附属科技中学2021-2022学年高二上学期期中考数学试题(已下线)第08练—2020年新高考数学小题冲刺卷(山东专用)-《2020年新高考政策解读与配套资源》湖南师大二附中2020-2021学年高三上学期第一次阶段性考试数学试题河北省邯郸市大名一中2020-2021学年高二上学期10月月考数学试题辽宁省大连市瓦房店市2020-2021学年高二上学期期中数学试题广东省深圳市福田区福田外国语学校2020-2021学年高二上学期期中数学试题河北省石家庄二中2021届高三上学期月考数学试题湖北省黄冈市黄梅国际育才高级中学2020-2021学年高二下学期3月月考数学试题河北省涞水波峰中学2020-2021学年高二上学期期末数学试题(已下线)卷12 选择性必修第一册高二上期中考试 总复习检测3(中)-2021-2022学年高二数学单元卷模拟(易中难)(2019人教A版选择性必修第一册+第二册)(已下线)专题9.7 圆锥曲线综合问题 2022年高考数学一轮复习讲练测(新教材新高考)(练)广东外语外贸大学实验中学2021-2022学年高二上学期期中数学试题(已下线)3.1.2椭圆的简单几何性质(备作业)-【上好课】2021-2022学年高二数学同步备课系列(人教A版2019选择性必修第一册)(已下线)专练35 综合拔高练-2021-2022学年高二数学上册同步课后专练(人版A版选择性必修第一册)四川省凉山州西昌市2021-2022学年高二上学期期末检测数学(文)试题重庆市西南大学附属中学校2021-2022学年高二上学期第二次月考数学试题沪教版(2020) 选修第一册 新课改一课一练 期中测试B江苏省泰州市民兴实验中学2021-2022学年高二上学期第一次月考数学试题安徽省合肥一六八中学2022-2023学年高二上学期期中数学试题甘肃省民勤县第一中学2022-2023学年高二下学期开学考试数学试题(已下线)3.1.2椭圆的标准方程及性质的应用(第2课时)辽宁省丹东市凤城市第一中学2023-2024学年高二上学期10月月考数学试题【巩固卷】期中复习B单元测试B沪教版(2020)选择性必修一
8 . 圆 :
: 上的动点
上的动点 在
在 轴、
轴、 轴上的射影分别是
轴上的射影分别是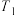 ,
, ,点
,点 满足
满足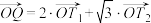 .
.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)点 ,
, 在轨迹
在轨迹 上且直线
上且直线 过点
过点 ,试问:是否存在定点
,试问:是否存在定点 ,使得
,使得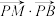 为定值?若存在,求
为定值?若存在,求 ;若不存在,请说明理由.
;若不存在,请说明理由.
 :
: 上的动点
上的动点 在
在 轴、
轴、 轴上的射影分别是
轴上的射影分别是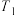 ,
, ,点
,点 满足
满足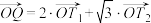 .
.(1)求点
 的轨迹
的轨迹 的方程;
的方程;(2)点
 ,
, 在轨迹
在轨迹 上且直线
上且直线 过点
过点 ,试问:是否存在定点
,试问:是否存在定点 ,使得
,使得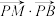 为定值?若存在,求
为定值?若存在,求 ;若不存在,请说明理由.
;若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
9 . 已知椭圆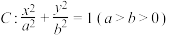 经过点
经过点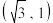 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)过点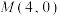 的直线交椭圆于
的直线交椭圆于 、
、 两点,若
两点,若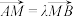 ,在线段
,在线段 上取点
上取点 ,使
,使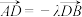 ,求证:点
,求证:点 在定直线上.
在定直线上.
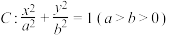 经过点
经过点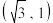 ,离心率为
,离心率为 .
.(1)求椭圆
 的方程;
的方程;(2)过点
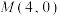 的直线交椭圆于
的直线交椭圆于 、
、 两点,若
两点,若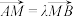 ,在线段
,在线段 上取点
上取点 ,使
,使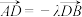 ,求证:点
,求证:点 在定直线上.
在定直线上.
您最近一年使用:0次
2020-03-29更新
|
2992次组卷
|
15卷引用:福建省厦门市海沧中学2019-2020学年高三四月强化检测(理科)数学试题
福建省厦门市海沧中学2019-2020学年高三四月强化检测(理科)数学试题2020届河北省沧州市高三一模数学(文)试题2020届河北省沧州市高三一模数学(理)试题(已下线)冲刺卷03-决战2020年高考数学冲刺卷(山东专版)广东省湛江市2019-2020学年高三下学期模拟数学(理)试题2020届北京市顺义牛栏山第一中学西校区高三下学期 4 月月考试卷数学试题(已下线)专题01 解析几何(第三篇)-备战2020高考数学黄金30题系列之压轴题(新课标版)(已下线)专题05 平面解析几何-2020年高三数学(文)3-4月模拟试题汇编(已下线)提升套餐练03-【新题型】2020年新高考数学多选题与热点解答题组合练山西省太原市第五中学2020届高三下学期6月月考数学(理)试题(已下线)专题20 圆锥曲线综合-2020年高考数学母题题源解密(北京专版)江西省南昌市第十中学2021届高三年级上学期第二次月考理科数学试题江西省南昌市第十中学2021届高三上学期第二次月考数学(文)试题(已下线)专题12 定比点差法及其应用 微点2 定比点差法综合应用(一)——解决定点、定值、定直线问题(已下线)拔高点突破01 定比点差法、齐次化、极点极线问题、蝴蝶问题、坎迪定理(五大题型)
名校
10 . 已知椭圆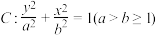 的离心率为
的离心率为 ,其上焦点到直线
,其上焦点到直线 的距离为
的距离为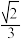 .
.
(1)求椭圆 的方程;
的方程;
(2)过点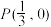 的直线
的直线 交椭圆
交椭圆 于
于 ,
, 两点.试探究以线段
两点.试探究以线段 为直径的圆是否过定点?若过,求出定点坐标,若不过,请说明理由.
为直径的圆是否过定点?若过,求出定点坐标,若不过,请说明理由.
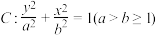 的离心率为
的离心率为 ,其上焦点到直线
,其上焦点到直线 的距离为
的距离为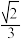 .
.(1)求椭圆
 的方程;
的方程;(2)过点
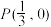 的直线
的直线 交椭圆
交椭圆 于
于 ,
, 两点.试探究以线段
两点.试探究以线段 为直径的圆是否过定点?若过,求出定点坐标,若不过,请说明理由.
为直径的圆是否过定点?若过,求出定点坐标,若不过,请说明理由.
您最近一年使用:0次
2018-12-29更新
|
900次组卷
|
4卷引用:福建省泉州市泉港区第一中学2018-2019学年高二年上学期期末考数学(理)试题



