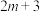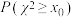1 . 已知 和
和 之间的一组数据如下表,
之间的一组数据如下表, 与
与 线性相关,且回归方程为
线性相关,且回归方程为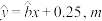 为
为 的方差的1.2倍,则当
的方差的1.2倍,则当 时,
时,
______ .
 和
和 之间的一组数据如下表,
之间的一组数据如下表, 与
与 线性相关,且回归方程为
线性相关,且回归方程为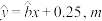 为
为 的方差的1.2倍,则当
的方差的1.2倍,则当 时,
时,
| 0 | 1 | 2 | 3 |
|
|
| 5 |
|
您最近一年使用:0次
解题方法
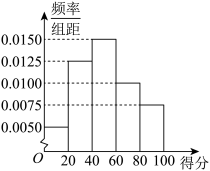
2 . 为加大自然生态系统和环境保护力度,加强企业对尊重自然、顺应自然、保护自然的生态文明理念,某市对化工企业的排污情况进行调查,并出台相应的整治措施.相关部门对1000家化工企业所排污水的质量及周围空气质量进行了综合检测,得分情况如频率分布直方图所示. (同一组中的数据以这组数据的中间值为代表);
(同一组中的数据以这组数据的中间值为代表);
(2)已知化工企业的得分情况 近似服从正态分布
近似服从正态分布 ,其中
,其中 ,则得分在
,则得分在 内的企业大约有多少家;
内的企业大约有多少家;
(3)按照(2)中概率分布随机抽取100家化工企业,分数不低于19分的企业有多少家时概率最大.
参考数据:若随机变量 服从正态分布
服从正态分布 ,则
,则 ,
,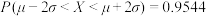 ,
,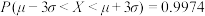 .
.
 (同一组中的数据以这组数据的中间值为代表);
(同一组中的数据以这组数据的中间值为代表);(2)已知化工企业的得分情况
 近似服从正态分布
近似服从正态分布 ,其中
,其中 ,则得分在
,则得分在 内的企业大约有多少家;
内的企业大约有多少家;(3)按照(2)中概率分布随机抽取100家化工企业,分数不低于19分的企业有多少家时概率最大.
参考数据:若随机变量
 服从正态分布
服从正态分布 ,则
,则 ,
,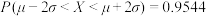 ,
,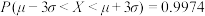 .
.
您最近一年使用:0次
解题方法
3 . 某外卖公司为提高外卖骑手的服务意识和服务水平,对骑手的服务水平进行了考核,并从中随机抽取了100名骑手,根据这100名骑手的服务水平评分制成如下的频率分布直方图,已知所有骑手的服务水平评分均在区间 内.
内. 及服务水平评分的平均数和中位数(同一组中的数据用该组数据的中间值为代表,结果保留1位小数);
及服务水平评分的平均数和中位数(同一组中的数据用该组数据的中间值为代表,结果保留1位小数);
(2)从服务水平评分在区间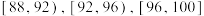 内的骑手中用分层抽样的方法抽取12人,再从这12人中随机抽取4人,记
内的骑手中用分层抽样的方法抽取12人,再从这12人中随机抽取4人,记 为4人中评分落在
为4人中评分落在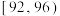 内的人数,求
内的人数,求 的分布列和期望.
的分布列和期望.
 内.
内.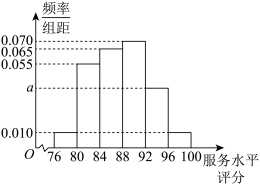
 及服务水平评分的平均数和中位数(同一组中的数据用该组数据的中间值为代表,结果保留1位小数);
及服务水平评分的平均数和中位数(同一组中的数据用该组数据的中间值为代表,结果保留1位小数);(2)从服务水平评分在区间
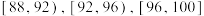 内的骑手中用分层抽样的方法抽取12人,再从这12人中随机抽取4人,记
内的骑手中用分层抽样的方法抽取12人,再从这12人中随机抽取4人,记 为4人中评分落在
为4人中评分落在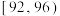 内的人数,求
内的人数,求 的分布列和期望.
的分布列和期望.
您最近一年使用:0次
4 . 2023年3月22日是第三十一届“世界水日”,3月22-28日是第三十六届“中国水周”.我国纪念2023年“世界水日”“中国水周”活动主题为“强化依法治水,携手共护母亲河”.为提高学生惜水爱水、节约护水的意识,某高中随机抽取了 人进行专项答题测试,数据如下表:
人进行专项答题测试,数据如下表:
若学生的答题测试成绩大于等于 分,则视为“护水意识强”,否则视为“护水意识薄弱”.
分,则视为“护水意识强”,否则视为“护水意识薄弱”.
(1)求该校高一、高二学生的专项答题测试成绩的中位数(保留1位小数);
(2)判断是否有 的把握认为护水意识与年级有关.
的把握认为护水意识与年级有关.
 人进行专项答题测试,数据如下表:
人进行专项答题测试,数据如下表:| 成绩 年级 |  |  |  |  |
| 高一 |  |  | 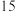 |  |
| 高二 |  |  | 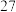 |  |
 分,则视为“护水意识强”,否则视为“护水意识薄弱”.
分,则视为“护水意识强”,否则视为“护水意识薄弱”.(1)求该校高一、高二学生的专项答题测试成绩的中位数(保留1位小数);
(2)判断是否有
 的把握认为护水意识与年级有关.
的把握认为护水意识与年级有关.
您最近一年使用:0次
5 . 近年来,随着社会对教育越来越重视,家庭的平均教育支出呈现出逐年增长的趋势,下表反映了2018-2022年某市家庭平均教育支出占家庭总支出的比例 (百分比)与年份编号
(百分比)与年份编号 之间的关系:
之间的关系:
则 与
与 的样本相关系数
的样本相关系数
______ (保留3位小数).
附: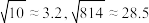 ,
,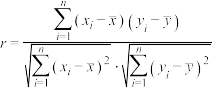 .
.
 (百分比)与年份编号
(百分比)与年份编号 之间的关系:
之间的关系:年份 | 2018 | 2019 | 2020 | 2021 | 2022 |
| 1 | 2 | 3 | 4 | 5 |
| 21 | 26 | 40 | 49 | 54 |
 与
与 的样本相关系数
的样本相关系数
附:
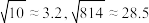 ,
,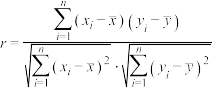 .
.
您最近一年使用:0次
解题方法
6 . 若随机变量 的方差为
的方差为 ,
, (
( 常数,且
常数,且 ),你能推导出
),你能推导出 与
与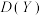 的关系吗?
的关系吗?
 的方差为
的方差为 ,
, (
( 常数,且
常数,且 ),你能推导出
),你能推导出 与
与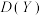 的关系吗?
的关系吗?
您最近一年使用:0次
解题方法
7 . 为了巩固拓展脱贫攻坚的成果,振兴乡村经济,某知名电商平台决定为脱贫乡村的特色水果开设直播带货专场.该特色水果的热卖黄金时段为7月10日至9月10日,为了解直播的效果和关注度,该电商平台统计了已直播的7月10日至7月14日时段中的相关数据,这5天中的第 天到该电商平台专营店购物的人数
天到该电商平台专营店购物的人数 (单位:万人)的数据如下表:
(单位:万人)的数据如下表:
参考数据: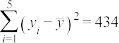 ,
,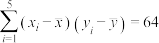 ,
,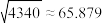 .
.
附:相关系数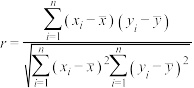 ,回归直线方程的斜率
,回归直线方程的斜率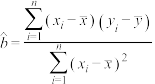 ,截距
,截距 .
.
(1)依据表中的统计数据,请判断该电商平台直播的第 天与到该电商平台专营店购物人数
天与到该电商平台专营店购物人数 (单位:万人)是否具有较高的线性相关程度?(参考:若
(单位:万人)是否具有较高的线性相关程度?(参考:若 ,则线性相关程度一般,若
,则线性相关程度一般,若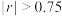 ,则线性相关程度较高,计算
,则线性相关程度较高,计算 时精确度为0.01)
时精确度为0.01)
(2)求购物人数 与直播的第
与直播的第 天的回归直线方程;用样本估计总体,请预测从7月10日起的第38天到该专营店购物的人数(单位:万人).
天的回归直线方程;用样本估计总体,请预测从7月10日起的第38天到该专营店购物的人数(单位:万人).
 天到该电商平台专营店购物的人数
天到该电商平台专营店购物的人数 (单位:万人)的数据如下表:
(单位:万人)的数据如下表:日期 | 7月10日 | 7月11日 | 7月12日 | 7月13日 | 7月14日 |
第 | 1 | 2 | 3 | 4 | 5 |
人数 | 75 | 84 | 93 | 98 | 100 |
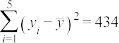 ,
,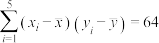 ,
,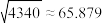 .
.附:相关系数
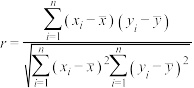 ,回归直线方程的斜率
,回归直线方程的斜率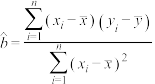 ,截距
,截距 .
.(1)依据表中的统计数据,请判断该电商平台直播的第
 天与到该电商平台专营店购物人数
天与到该电商平台专营店购物人数 (单位:万人)是否具有较高的线性相关程度?(参考:若
(单位:万人)是否具有较高的线性相关程度?(参考:若 ,则线性相关程度一般,若
,则线性相关程度一般,若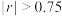 ,则线性相关程度较高,计算
,则线性相关程度较高,计算 时精确度为0.01)
时精确度为0.01)(2)求购物人数
 与直播的第
与直播的第 天的回归直线方程;用样本估计总体,请预测从7月10日起的第38天到该专营店购物的人数(单位:万人).
天的回归直线方程;用样本估计总体,请预测从7月10日起的第38天到该专营店购物的人数(单位:万人).
您最近一年使用:0次
8 . 下列说法中错误的是( )
| A.将一组数据中的每一个数据都加上或减去同一个常数后,方差不变 |
B.对于回归直线方程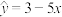 ,变量 ,变量 增加1个单位时, 增加1个单位时, 平均增加5个单位 平均增加5个单位 |
C.回归直线 必过点 必过点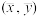 |
D.设具有相关关系的两个变量 , , 的相关系数为 的相关系数为 ,则 ,则 越接近于0, 越接近于0, , , 之间的线性相关程度越强 之间的线性相关程度越强 |
您最近一年使用:0次
解题方法
9 . 为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查,得到了如下的统计结果.
表1:男生上网时间与频率分布表
表2:女生上网时间与频率分布表
(1)若该大学生共有女生750人,试估计其中上网时间不少于60分钟的人数;
(2)完成下面的2×2列联表,并回答根据小概率值 的独立性检验,能否认为“大学生上网时间与性别有关”.
的独立性检验,能否认为“大学生上网时间与性别有关”.
附 ,其中
,其中
 为样本容量.
为样本容量.
表1:男生上网时间与频率分布表
上网时间(分) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
人数 | 5 | 25 | 30 | 25 | 15 |
上网时间(分) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
人数 | 10 | 20 | 40 | 20 | 10 |
(2)完成下面的2×2列联表,并回答根据小概率值
 的独立性检验,能否认为“大学生上网时间与性别有关”.
的独立性检验,能否认为“大学生上网时间与性别有关”.上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
男生 | |||
女生 | |||
合计 |
 ,其中
,其中
 为样本容量.
为样本容量.
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
10 . 某市对机动车单双号限行进行了调查,在参加调查的2600名有车人中有1700名持反对意见,2500名无车人中有1400名持反对意见,在运用这些数据说明“拥有车辆”与“反对机动车单双号限行”是否相关时,用下列哪种方法最有说服力( )
| A.独立性检验 | B.数学期望 | C.随机误差 | D.频率分布直方图 |
您最近一年使用:0次