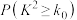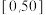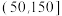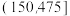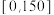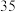型机床,该型机床已投入生产的时间
型机床,该型机床已投入生产的时间 (单位:年)与当年所需要支出的维修费用
(单位:年)与当年所需要支出的维修费用 (单位:万元)有如下统计资料:
(单位:万元)有如下统计资料:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
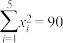 ,
, ,
,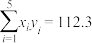 ,
,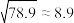 ,
,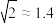
(1)计算
 与
与 的样本相关系数
的样本相关系数 (精确到0.001),并判断该型机床的使用年限与所支出的维修费用的相关性强弱(若
(精确到0.001),并判断该型机床的使用年限与所支出的维修费用的相关性强弱(若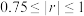 ,则认为
,则认为 与
与 相关性很强,否则不强).
相关性很强,否则不强).(2)该厂购入一台新的
 型机床,工人们分别使用这台机床(记为
型机床,工人们分别使用这台机床(记为 )和一台已经使用多年的
)和一台已经使用多年的 型机床(记为
型机床(记为 )各制造50个零件,统计得出的数据如下表:
)各制造50个零件,统计得出的数据如下表:机床 | 零件 | 合计 | |
合格 | 不合格 | ||
| 4 | ||
| 40 | ||
合计 | |||
 列联表补充完整,并判断是否有99%的把握认为“零件合格情况是否与机床的使用情况有关”.
列联表补充完整,并判断是否有99%的把握认为“零件合格情况是否与机床的使用情况有关”.附参考公式及数据
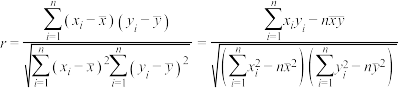
 ,其中
,其中 .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
课余学习时间超过两小时 | 课余学习时间不超过两小时 | |
200名以前 | 40 |
|
200名以后 |
| 40 |
(2)依据上表,判断是否有99.9%的把握认为,高三学生课余学习时间超过两小时跟学生成绩有关;
(3)学校在成绩200名以前的学生中,采用分层抽样,按课余学习时间是否超过两小时抽取6人,再从这6人中随机抽取3人,记这3人中课余学习时间超过两小时的学生人数为X,求X的分布列和数学期望.
附:参考公式:
 ,其中
,其中 .
.a | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
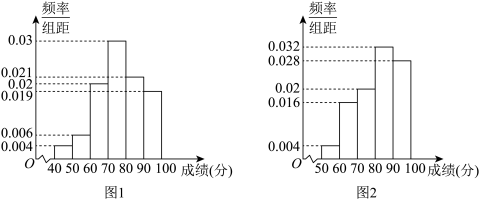
(2)我们规定得分80分以上(含80分)的为“优秀”,低于80分的为“非优秀”.
优秀人数 | 非优秀人数 | 合计 | |
强化训练前 | |||
强化训练后 | |||
合计 |
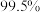 的把握认为跳水运动员是否优秀与强化训练有关.
的把握认为跳水运动员是否优秀与强化训练有关.附:
 .
.
| 0.05 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 |  | |
| 乙班 |  | 30 |
 ,则下列说法正确的是
,则下列说法正确的是①列联表中
 的值为
的值为 的值为40;
的值为40;②列联表中
 的值为
的值为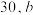 的值为50;
的值为50;③根据列联表中的数据,若按
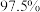 的可靠性要求,能认为“成绩与班级有关系”;
的可靠性要求,能认为“成绩与班级有关系”;④根据列联表中的数据,若按
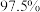 的可靠性要求,不能认为“成绩与班级有关系”.
的可靠性要求,不能认为“成绩与班级有关系”.附:
 ,其中
,其中 .
. | 0.15 | 0.1 | 0.05 | 0.025 | 0.01 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
场次编号 | 1 | 2 | 3 | 4 | 5 |
观众人数 | 0.7 | 0.8 | 1 | 1.2 | 1.3 |
 与
与 的关系,请建立
的关系,请建立 关于
关于 的线性回归方程;
的线性回归方程;(2)若该烟花秀节目分A、B、C三个等次的票价,某机构随机调查了该烟花秀节目现场200位观众的性别与购票情况,得到的部分数据如表所示,请将
 列联表补充完整,并判断能否有
列联表补充完整,并判断能否有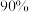 的把握认为该烟花秀节目的观众是否购买A等票与性别有关.
的把握认为该烟花秀节目的观众是否购买A等票与性别有关.购买A等票 | 购买非A等票 | 总计 | |
男性观众 | 50 | ||
女性观众 | 60 | ||
总计 | 100 | 200 |
 中斜率与截距的最小二乘法估计公式分别为
中斜率与截距的最小二乘法估计公式分别为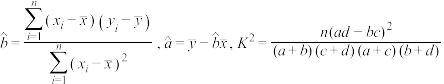 ,其中
,其中 .
.
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
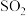 的浓度(单位:
的浓度(单位: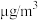 ),整理数据得到下表:
),整理数据得到下表:
空气质量等级 |
|
|
|
1(优) | 84 | 18 | 6 |
2(良) | 15 | 21 | 24 |
3(轻度污染) | 9 | 24 | 27 |
4(中度污染) | 3 | 36 | 33 |
(1)完成下面的
 列联表:
列联表:
空气质量 |
|
| 合计 |
空气质量好 | |||
空气质量不好 | |||
合计 |
 的把握认为该市一天的空气质量与当天
的把握认为该市一天的空气质量与当天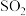 的浓度有关?
的浓度有关?附:
 ;
;
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
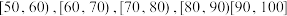 )
)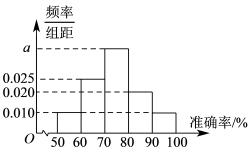
 的值,并完成下面的
的值,并完成下面的 列联表;
列联表;| 大型数据集 | 小型数据集 | 合计 | |
| 达标 | 30 | ||
| 不达标 | |||
| 合计 |
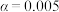 的独立性检验,能否认为语言模型准确率是否达标与使用的训练数据集大小有关联?
的独立性检验,能否认为语言模型准确率是否达标与使用的训练数据集大小有关联?附:
 其中
其中
 | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
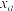 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
| 得分 | 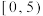 | 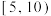 | 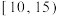 | 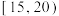 | 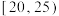 | 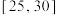 |
| 人数 | 2 | 3 | 4 | 6 | 4 | 1 |
(1)请根据上述表格中的统计数据,将下面的
 列联表补充完全,并通过计算判断在20位新成员中,是否有
列联表补充完全,并通过计算判断在20位新成员中,是否有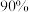 的把握认为“获奖”与性别有关?
的把握认为“获奖”与性别有关?| 没获奖 | 获奖 | 合计 | |
| 男 | 4 | ||
| 女 | 7 | 8 | |
| 合计 |
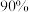 的把握认为“获奖”与性别有关.请判断这5名老成员的性别?
的把握认为“获奖”与性别有关.请判断这5名老成员的性别?附:参考公式:
 .
.临界值表:
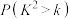 | 0.100 | 0.050 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 10.828 |
 年
年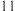 月
月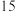 日
日 时
时 分,长征四号丙运载火箭在酒泉卫星发射中心点火起飞,随后将遥感三十四号
分,长征四号丙运载火箭在酒泉卫星发射中心点火起飞,随后将遥感三十四号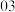 星送入预定轨道发射,大量观众通过某网络直播平台观看了发射全过程.为了解大家是否关注航空航天技术,该平台随机抽取了
星送入预定轨道发射,大量观众通过某网络直播平台观看了发射全过程.为了解大家是否关注航空航天技术,该平台随机抽取了 名用户进行调查,相关数据如下表.
名用户进行调查,相关数据如下表.关注 | 不关注 | 合计 | |
男性用户 |
| ||
女性用户 |
|
| |
合计 |
|
(2)能否有
 的把握认为是否关注航空航天技术与性别有关?
的把握认为是否关注航空航天技术与性别有关?附:
 ,
, .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
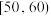 ,
,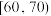 ,
,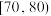 ,
,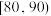 ,
, ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
(1)估计这100名学生的竞赛成绩的中位数(结果保留整数);
(2)在抽取的100名学生中,规定:竞赛成绩不低于70分为“优秀”,竞赛成绩低于70分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“竞赛成绩是否优秀与性别有关”?(精确到0.001)
优秀 | 非优秀 | 合计 | |
男 | 30 | ||
女 | 50 | ||
合计 | 100 |
 ,其中
,其中 .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |