2023·广东肇庆·二模
名校
解题方法
1 . 随着春节的临近,小王和小张等4位同学准备互相送祝福.他们每人写了一个祝福的贺卡,这四张贺卡收齐后让每人从中随机抽取一张作为收到的新春祝福,则( )
A.小王和小张恰好互换了贺卡的概率为 |
B.已知小王抽到的是小张写的贺卡的条件下,小张抽到小王写的贺卡的概率为 |
C.恰有一个人抽到自己写的贺卡的概率为 |
D.每个人抽到的贺卡都不是自己写的概率为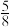 |
您最近一年使用:0次
2023-01-10更新
|
5491次组卷
|
14卷引用:第七章 随机变量及其分布 (单元测)
(已下线)第七章 随机变量及其分布 (单元测)(已下线)8.1.1 条件概率(2)云南省红河州开远市第一中学校2022-2023学年高二下学期4月月考数学试题(已下线)3.1.1 条件概率(同步练习)2022-2023学年高二选择性必修第二册素养提升检测(基础篇)专题12排列组合与计数原理专题14条件概率与全概率公式广东省肇庆市2023届高三第二次教学质量检测数学试题广东省广州市大湾区2023届高三第一次联合模拟数学试题(已下线)模块七 计数原理与统计概率-3(已下线)专题10 计数原理与概率统计(理科)(已下线)模块八 专题5 以概率与统计为背景的压轴小题专题22计数原理与概率与统计(多选题)江苏省镇江第一中学2023-2024学年高三上学期期初学情检测数学试题广东省肇庆市封开县江口中学2024届高三上学期第四次月考数学试题
2023·湖南·一模
名校
解题方法
2 . 下列说法正确的是( )
A.已知随机变量 服从二项分布: 服从二项分布: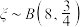 ,设 ,设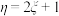 ,则 ,则 的方差 的方差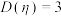 |
B.数据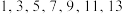 的第60百分位数为9 的第60百分位数为9 |
C.若样本数据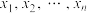 的平均数为2,则 的平均数为2,则 的平均数为8 的平均数为8 |
D.用简单随机抽样的方法从51个个体中抽取2个个体,则每个个体被抽到的概率都是 |
您最近一年使用:0次
2023-12-02更新
|
2217次组卷
|
4卷引用:6.4.1二项分布(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)
(已下线)6.4.1二项分布(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)2024届湖南省高三九校联盟第一次联考数学试卷江苏省苏州市西交大苏州附中2024届高三上学期12月月考数学试题河南省安阳市林州市第一中学2024届高三上学期期末数学试题
名校
解题方法
3 . 疫情当下,通过直播带货来助农,不仅为更多年轻人带来了就业岗位,同时也为当地农民销售出了农产品,促进了当地的经济发展.某直播平台的主播现要对6种不同的脐橙进行选品,其方法为首先对这6种不同的脐橙(数量均为1),进行标号为1~6,然后将其放入一个箱子中,从中有放回的随机取两次,每次取一个脐橙,记第一次取出的脐橙的标号为 ,第二次为
,第二次为 ,设
,设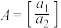 ,其中[x]表示不超过x的最大整数,则( )
,其中[x]表示不超过x的最大整数,则( )
 ,第二次为
,第二次为 ,设
,设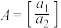 ,其中[x]表示不超过x的最大整数,则( )
,其中[x]表示不超过x的最大整数,则( )A. | B.事件 与 与 互斥 互斥 |
C.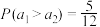 | D.事件 与 与 对立 对立 |
您最近一年使用:0次
2023-01-05更新
|
1961次组卷
|
13卷引用:湖北省荆州市八县市2022-2023学年高二上学期期末联考数学试题
湖北省荆州市八县市2022-2023学年高二上学期期末联考数学试题陕西省西安市铁一中学2022-2023学年高二上学期1月期末数学试题四川省眉山市东坡区多悦高级中学校等2023-2024学年高二上学期期中联考数学试题海南省海口市海南中学2023-2024学年高二上学期期末考试数学试题 四川省泸县第五中学2023-2024学年高二上学期第一次月考试数学试题(已下线)专题10.9 概率全章综合测试卷(提高篇)-2022-2023学年高一数学举一反三系列(人教A版2019必修第二册)第十章《概率》单元达标高分突破必刷卷(培优版)-《考点·题型·技巧》(已下线)模块四 专题6 暑期结束综合检测6(能力卷)辽宁省本溪市高级中学2023-2024学年高三上学期高考适应性测试(一)数学试题单元测试A卷——第十章?概率(已下线)高一下学期期末数学试卷(提高篇)-举一反三系列(人教A版2019必修第二册)(已下线)第06讲 第十章 概率 章末题型大总结-【帮课堂】(人教A版2019必修第二册)(已下线)专题24 事件的相互独立性 频率与概率-《重难点题型·高分突破》(人教A版2019必修第二册)
名校
解题方法
4 . 某短视频平台以讲故事,赞家乡,聊美食,展才艺等形式展示了丰富多彩的新时代农村生活,吸引了众多粉丝,该平台通过直播带货把家乡的农产品推销到全国各地,从而推进了“新时代乡村振兴”.从平台的所有主播中,随机选取300人进行调查,其中青年人,中年人,其他人群三个年龄段的比例饼状图如图1所示,各年龄段主播的性别百分比等高堆积条形图如图2所示,则下列说法正确的有( )
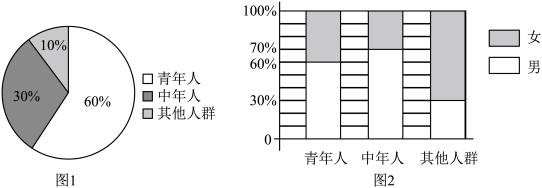

| A.该平台女性主播占比的估计值为0.4 |
| B.从所调查的主播中,随机抽取一位参加短视频剪辑培训,则被抽到的主播是中年男性的概率为0.7 |
| C.按年龄段把所调查的主播分为三层,用分层抽样法抽取20名主播担当平台监管,若样本量按比例分配,则中年主播应抽取6名 |
| D.从所调查的主播中,随机选取一位做为幸运主播,已知该幸运主播是青年人的条件下,又是女性的概率为0.6 |
您最近一年使用:0次
2023-04-21更新
|
2054次组卷
|
10卷引用:湖北省孝感市部分学校2023-2024学年高二上学期9月起点考试数学试题
湖北省孝感市部分学校2023-2024学年高二上学期9月起点考试数学试题浙江省余姚中学2023-2024学年高二上学期期中考试数学试卷山东省聊城市2023届高三二模数学试题江苏省南通市海安高级中学2023届高三下学期阶段检测(五)数学试题(已下线)模块六 专题2 易错题目重组卷(山东卷)(已下线)押新高考第9题 概率统计与随机变量分布列及期望方差专题22计数原理与概率与统计(多选题)(已下线)情境5 关注生产生活山东省烟台市中英文高级中学2023届高考模拟预测数学试题(已下线)模块一 专题4 《概率和分布》单元检测篇 A基础卷
名校
5 . 红黄蓝被称为三原色,选取任意几种颜色调配,可以调配出其他颜色.已知同一种颜色混合颜色不变,等量的红色加黄色调配出橙色;等量的红色加蓝色调配出紫色;等量的黄色加蓝色调配出绿色.现有红黄蓝彩色颜料各两瓶,甲从六瓶中任取两瓶颜料,乙再从余下四瓶中任取两瓶颜料,两人分别进行等量调配,A表示事件“甲调配出红色”;B表示事件“甲调配出绿色”;C表示事件“乙调配出紫色”,则下列说法正确的是( ).
| A.事件A与事件C是独立事件 | B.事件A与事件B是互斥事件 |
C. | D. |
您最近一年使用:0次
2023-03-13更新
|
1999次组卷
|
5卷引用:湖南师范大学附属中学2022-2023学年高二下学期期中数学试题
湖南师范大学附属中学2022-2023学年高二下学期期中数学试题重庆市2023届高三第七次质量检测数学试题重庆市南开中学校2023届高三第七次质量检测数学试题(已下线)押新高考第9题 概率统计与随机变量分布列及期望方差(已下线)模块六 专题8 易错题目重组卷(重庆卷)
2021·山东滨州·二模
名校
6 . 为庆祝建党100周年,讴歌中华民族实现伟大复兴的奋斗历程,增进全体党员干部职工对党史知识的了解,某单位组织开展党史知识竞赛活动,以支部为单位参加比赛,某支部在5道党史题中(有3道选择题和 道填空题),不放回地依次随机抽取
道填空题),不放回地依次随机抽取 道题作答,设事件A为“第1次抽到选择题”,事件B为“第
道题作答,设事件A为“第1次抽到选择题”,事件B为“第 次抽到选择题”,则下列结论中正确的是( )
次抽到选择题”,则下列结论中正确的是( )
 道填空题),不放回地依次随机抽取
道填空题),不放回地依次随机抽取 道题作答,设事件A为“第1次抽到选择题”,事件B为“第
道题作答,设事件A为“第1次抽到选择题”,事件B为“第 次抽到选择题”,则下列结论中正确的是( )
次抽到选择题”,则下列结论中正确的是( )A.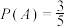 | B.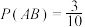 |
C.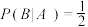 | D. |
您最近一年使用:0次
2021-05-14更新
|
5518次组卷
|
18卷引用:【新教材精创】第七章 随机变量及其分布--复习与小结 -A基础练
(已下线)【新教材精创】第七章 随机变量及其分布--复习与小结 -A基础练(已下线)【新教材精创】7.1.1 条件概率 -B提高练江苏省南京市金陵中学2020-2021学年高二下学期期末数学试题人教B版(2019) 选修第二册 突围者 第四章 第一节 课时1 条件概率(已下线)选择性必修三综合测试(一)-【上好课】2020-2021学年高二数学同步备课系列(人教A版2019选择性必修第三册)(已下线)第四章 概率与统计 4.1 条件概率与事件的独立性 4.1.1 条件概率苏教版(2019) 选修第二册 名师精选 第八章 第五单元 条件概率人教A版(2019) 选修第三册 名师精选 第三单元 条件概率与全概率公式山西省实验中学2022-2023学年高二下学期第一次月考数学试题辽宁省重点高中沈阳市郊联体2023-2024学年高二上学期1月期末考试数学试题(已下线)第01讲 7.1.1条件概率-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)陕西省西安市蓝田县城关中学大学区联考2023-2024学年高二下学期3月阶段性学习效果评测数学试题(已下线)7.1.1 条件概率——课后作业(基础版)山东省滨州市2021届高三二模(5月)数学试题(已下线)8.2 古典概型与条件概率(精练)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)(已下线)考点73 章末检测十一-备战2022年高考数学一轮复习考点帮(新高考地区专用)【学科网名师堂】重庆市万州第二高级中学2023届高三下学期第二次诊断数学试题甘肃省庆阳市华池县第一中学2022-2023学年高一下学期期中数学试题
名校
解题方法
7 . 小张等四人去甲、乙、丙三个景点旅游,每人只去一个景点,记事件A为“恰有两人所去景点相同”,事件 为“只有小张去甲景点”,则( )
为“只有小张去甲景点”,则( )
 为“只有小张去甲景点”,则( )
为“只有小张去甲景点”,则( )| A.这四人不同的旅游方案共有64种 | B.“每个景点都有人去”的方案共有72种 |
C.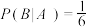 | D.“四个人只去了两个景点”的概率是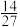 |
您最近一年使用:0次
2023-10-20更新
|
1455次组卷
|
7卷引用:黑龙江省双鸭山市第一中学2023-2024学年高二上学期12月月考数学试题
黑龙江省双鸭山市第一中学2023-2024学年高二上学期12月月考数学试题陕西省渭南市韩城市象山中学2023-2024学年高二上学期第三次月考数学试题(已下线)6.1.1条件概率的概念(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)(已下线)4.1.1 条件概率(分层练习)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第二册)河南省平许济洛2023-2024学年高三上学期第一次质量检测数学试题福建省莆田市第二十五中学2023-2024学年高三上学期期中数学试题海南省儋州市洋浦中学2024届高三上学期第四次月考数学试题
名校
8 . 某中药材盒中共有包装相同的7袋药材,其中党参有3袋,黄芪有4袋,从中取出两袋,下列说法正确的是( )
A.若有放回抽取,则取出一袋党参一袋黄芪的概率为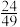 |
B.若有放回抽取,则在至少取出一袋党参的条件下,第2次取出党参的概率为 |
C.若不放回抽取,则第2次取到党参的概率算法可以是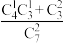 |
D.若不放回抽取,则在至少取出一袋党参的条件下,取到一袋党参一袋黄芪的概率为 |
您最近一年使用:0次
名校
解题方法
9 . 某研究机构为了探究吸烟与肺气肿是否有关,调查了200人.统计过程中发现随机从这200人中抽取一人,此人为肺气肿患者的概率为0.1.在制定 列联表时,由于某些因素缺失了部分数据,而获得如图所示的
列联表时,由于某些因素缺失了部分数据,而获得如图所示的 列联表,下列结论正确的是( )
列联表,下列结论正确的是( )
参考公式与临界值表:
 列联表时,由于某些因素缺失了部分数据,而获得如图所示的
列联表时,由于某些因素缺失了部分数据,而获得如图所示的 列联表,下列结论正确的是( )
列联表,下列结论正确的是( )| 患肺气肿 | 不患肺气肿 | 合计 | |
| 吸烟 | 15 | ||
| 不吸烟 | 120 | ||
| 合计 | 200 |

 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A.不吸烟患肺气肿的人数为5人 | B.200人中患肺气肿的人数为10人 |
C. 的观测值 的观测值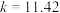 | D.按99.9%的可靠性要求,可以认为“吸烟与肺气肿有关系” |
您最近一年使用:0次
2023-04-05更新
|
1304次组卷
|
2卷引用:江苏省连云港市灌南高级中学2022-2023学年高二下学期第二次月考数学试题
解题方法
10 . 如图,某高速服务区停车场中有A至H共8个停车位(每个车位只能停一辆车),现有2辆黑色车和2辆白色车要在该停车场停车,则( )
A | B | C | D |
E | F | G | H |
| A.4辆车的停车方法共有1680种 |
B.4辆车恰好停在同一行的概率是 |
| C.2辆黑色车恰好相邻(停在同一行或同一列)的停车方法共有300种 |
D.相同颜色的车不停在同一行,也不停在同一列的概率是 |
您最近一年使用:0次



