1 . 当正态密度函数中的 一定时,曲线的形状由
一定时,曲线的形状由 确定.
确定.
即当 越大时,曲线变“矮胖”,表示总体的分布向
越大时,曲线变“矮胖”,表示总体的分布向 的两边
的两边__________ ;
当 越小时,曲线变“高瘦”,表示总体的分布向中心
越小时,曲线变“高瘦”,表示总体的分布向中心 处
处__________ .
 一定时,曲线的形状由
一定时,曲线的形状由 确定.
确定.即当
 越大时,曲线变“矮胖”,表示总体的分布向
越大时,曲线变“矮胖”,表示总体的分布向 的两边
的两边当
 越小时,曲线变“高瘦”,表示总体的分布向中心
越小时,曲线变“高瘦”,表示总体的分布向中心 处
处
您最近一年使用:0次
2 . 通常说正态分布集中在其期望 的附近,即参数
的附近,即参数 表示分布
表示分布__________ 的位置;参数 描述的是分布的
描述的是分布的__________ 程度.
 的附近,即参数
的附近,即参数 表示分布
表示分布 描述的是分布的
描述的是分布的
您最近一年使用:0次
3 . 正态密度函数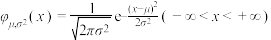 图像也称为钟形曲线,现有以下结论:
图像也称为钟形曲线,现有以下结论:
①曲线在 轴的上方,与
轴的上方,与 轴不相交;
轴不相交;
②曲线是单峰的,它关于直线 对称;
对称;
③曲线在 处达到峰值
处达到峰值 (最高点);
(最高点);
④当 无限增大时,曲线无限接近
无限增大时,曲线无限接近 轴;
轴;
⑤ 轴与正态曲线所夹面积恒等于1.
轴与正态曲线所夹面积恒等于1.
其中所有正确的结论序号为__________ .
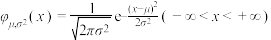 图像也称为钟形曲线,现有以下结论:
图像也称为钟形曲线,现有以下结论:①曲线在
 轴的上方,与
轴的上方,与 轴不相交;
轴不相交;②曲线是单峰的,它关于直线
 对称;
对称;③曲线在
 处达到峰值
处达到峰值 (最高点);
(最高点);④当
 无限增大时,曲线无限接近
无限增大时,曲线无限接近 轴;
轴;⑤
 轴与正态曲线所夹面积恒等于1.
轴与正态曲线所夹面积恒等于1.其中所有正确的结论序号为
您最近一年使用:0次
名校
4 . 某班级共有 40 名同学, 其中 15 人是团员. 现从该班级通过抽签选择 10 名同学参加活动,定义随机变量 为其中团员的人数,则
为其中团员的人数,则  服从 ( )
服从 ( )
 为其中团员的人数,则
为其中团员的人数,则  服从 ( )
服从 ( )| A.二项分布 | B.超几何分布 | C.正态分布 | D.伯努利分布 |
您最近一年使用:0次
5 . 某班级测验均分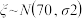 ,根据检测结果可知
,根据检测结果可知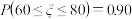 ,若该班级40名学生,则60分以下的人数大约为
,若该班级40名学生,则60分以下的人数大约为__________ .
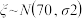 ,根据检测结果可知
,根据检测结果可知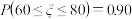 ,若该班级40名学生,则60分以下的人数大约为
,若该班级40名学生,则60分以下的人数大约为
您最近一年使用:0次
名校
6 . 当前新能源汽车已经走进我们的生活,主要部件是电池,一般地电池的生产工艺和过程条件要去较高,一般一块电池充满电后可连续正常工作的时间(小时)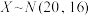 ,若检测到
,若检测到 则视为产品合格,否则进行维护,维护费用为3万元/块,近一年来由于受极端天气影响,某汽车制造公司技术部门加急对生产的一大批汽车电池随机抽取10个进行抽样检测,结果发现
则视为产品合格,否则进行维护,维护费用为3万元/块,近一年来由于受极端天气影响,某汽车制造公司技术部门加急对生产的一大批汽车电池随机抽取10个进行抽样检测,结果发现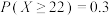 .
.
(1)求出10个样品中有几个不合格产品;
(2)若从10 个样品中随机抽取3件,记抽到的不合格产品个数为 ,求其分布列;
,求其分布列;
(3)若以样本频率估计总体,从本批次的产品中再抽取200块进行检测,记不合格品的个数为 ,预计会支出多少维护费
,预计会支出多少维护费 元?
元?
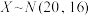 ,若检测到
,若检测到 则视为产品合格,否则进行维护,维护费用为3万元/块,近一年来由于受极端天气影响,某汽车制造公司技术部门加急对生产的一大批汽车电池随机抽取10个进行抽样检测,结果发现
则视为产品合格,否则进行维护,维护费用为3万元/块,近一年来由于受极端天气影响,某汽车制造公司技术部门加急对生产的一大批汽车电池随机抽取10个进行抽样检测,结果发现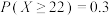 .
.(1)求出10个样品中有几个不合格产品;
(2)若从10 个样品中随机抽取3件,记抽到的不合格产品个数为
 ,求其分布列;
,求其分布列;(3)若以样本频率估计总体,从本批次的产品中再抽取200块进行检测,记不合格品的个数为
 ,预计会支出多少维护费
,预计会支出多少维护费 元?
元?
您最近一年使用:0次
2024-04-16更新
|
1140次组卷
|
5卷引用:上海市复旦中学2023-2024学年高二下学期5月月考数学试卷
上海市复旦中学2023-2024学年高二下学期5月月考数学试卷广东省珠海市第二中学2023-2024学年高二下学期第一阶段考试数学试题(已下线)7.5 正态分布(6大题型)精练-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)河北省邯郸市大名县大名中学2023—2024学年高二下学期期中考试数学试题山东省菏泽市鄄城县2023-2024学年高二下学期6月月考数学试题
名校
7 . 象棋是中国棋文化之一,也是中华民族的文化瑰宝,源远流长,雅俗共赏.某地举办象棋比赛,规定:每一局比赛中胜方得1分,负方得0分,没有平局.
(1)若甲、乙两名选手进行象棋比赛冠亚军的激烈角逐,每局比赛甲获胜的概率是 ,乙获胜的概率是
,乙获胜的概率是 ,先得3分者夺冠,比赛结束.
,先得3分者夺冠,比赛结束.
(i)求比赛结束时,恰好进行了3局的概率;
(ii)若前两局甲、乙各胜一局,记 表示到比赛结束还需要进行的局数,求
表示到比赛结束还需要进行的局数,求 的分布列及数学期望;
的分布列及数学期望;
(2)统计发现,本赛季参赛选手总得分 近似地服从正态分布
近似地服从正态分布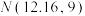 .若
.若 ,则参赛选手可获得“参赛纪念证书”;若
,则参赛选手可获得“参赛纪念证书”;若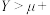
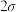 ,则参赛选手可获得“优秀参赛选手证书”.若共有200名选手参加本次比赛,试估计获得“参赛纪念证书”的选手人数.(结果保留整数)
,则参赛选手可获得“优秀参赛选手证书”.若共有200名选手参加本次比赛,试估计获得“参赛纪念证书”的选手人数.(结果保留整数)
附:若 ,则
,则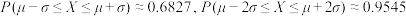 ,
,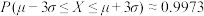 .
.
(1)若甲、乙两名选手进行象棋比赛冠亚军的激烈角逐,每局比赛甲获胜的概率是
 ,乙获胜的概率是
,乙获胜的概率是 ,先得3分者夺冠,比赛结束.
,先得3分者夺冠,比赛结束.(i)求比赛结束时,恰好进行了3局的概率;
(ii)若前两局甲、乙各胜一局,记
 表示到比赛结束还需要进行的局数,求
表示到比赛结束还需要进行的局数,求 的分布列及数学期望;
的分布列及数学期望;(2)统计发现,本赛季参赛选手总得分
 近似地服从正态分布
近似地服从正态分布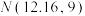 .若
.若 ,则参赛选手可获得“参赛纪念证书”;若
,则参赛选手可获得“参赛纪念证书”;若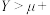
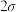 ,则参赛选手可获得“优秀参赛选手证书”.若共有200名选手参加本次比赛,试估计获得“参赛纪念证书”的选手人数.(结果保留整数)
,则参赛选手可获得“优秀参赛选手证书”.若共有200名选手参加本次比赛,试估计获得“参赛纪念证书”的选手人数.(结果保留整数)附:若
 ,则
,则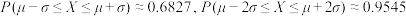 ,
,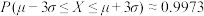 .
.
您最近一年使用:0次
2024-03-08更新
|
1333次组卷
|
3卷引用:第七章 概率初步(续)(知识归纳+题型突破)(3)
名校
8 . 某产品的尺寸与标准尺寸的误差绝对值不超过4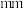 即视为合格品,否则视为不合格品.假设误差服从正态分布且每件产品是否为合格品相互独立.现随机抽取100件产品,误差的样本均值为0,样本方差为4.用样本估计总体.
即视为合格品,否则视为不合格品.假设误差服从正态分布且每件产品是否为合格品相互独立.现随机抽取100件产品,误差的样本均值为0,样本方差为4.用样本估计总体.
(1)试估计100件产品中不合格品的件数(精确到1);
(2)在(1)的条件下,现出售随机包装的100箱该产品,每箱均有100件产品.收货方对每箱产品均采取不放回地随机抽取方式进行检验,箱与箱之间的检验相互独立.每箱按以下规则判断是否接受该箱产品:如果抽检的第1件产品不合格,则拒绝该箱产品;如果抽检的第1件产品合格,则再抽1件,如果抽检的第2件产品合格,则接受该箱产品,否则拒绝该箱产品.若该箱产品通过检验后生产方获利1000元;该箱产品被拒绝,则亏损89元.求100箱该产品利润的期望值.
附:若随机变量 服从正态分布
服从正态分布 ,则
,则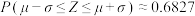 ,
,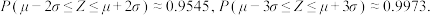
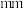 即视为合格品,否则视为不合格品.假设误差服从正态分布且每件产品是否为合格品相互独立.现随机抽取100件产品,误差的样本均值为0,样本方差为4.用样本估计总体.
即视为合格品,否则视为不合格品.假设误差服从正态分布且每件产品是否为合格品相互独立.现随机抽取100件产品,误差的样本均值为0,样本方差为4.用样本估计总体.(1)试估计100件产品中不合格品的件数(精确到1);
(2)在(1)的条件下,现出售随机包装的100箱该产品,每箱均有100件产品.收货方对每箱产品均采取不放回地随机抽取方式进行检验,箱与箱之间的检验相互独立.每箱按以下规则判断是否接受该箱产品:如果抽检的第1件产品不合格,则拒绝该箱产品;如果抽检的第1件产品合格,则再抽1件,如果抽检的第2件产品合格,则接受该箱产品,否则拒绝该箱产品.若该箱产品通过检验后生产方获利1000元;该箱产品被拒绝,则亏损89元.求100箱该产品利润的期望值.
附:若随机变量
 服从正态分布
服从正态分布 ,则
,则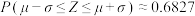 ,
,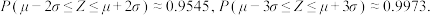
您最近一年使用:0次
2024-03-07更新
|
993次组卷
|
4卷引用:第七章 概率初步(续)(知识归纳+题型突破)(3)
(已下线)第七章 概率初步(续)(知识归纳+题型突破)(3)安徽省江南十校2024届高三3月联考数学试卷(已下线)第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)辽宁省锦州市某校2023-2024学年高三下学期考前测试数学试卷(A)
9 . 设 为任取的某袋有包装误差的产品的质量,
为任取的某袋有包装误差的产品的质量, 分别求
分别求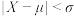 ,
, 及
及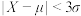 的概率.(结果精确到
的概率.(结果精确到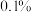 ,
,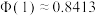 ,
,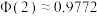 ,
, ).
).
 为任取的某袋有包装误差的产品的质量,
为任取的某袋有包装误差的产品的质量, 分别求
分别求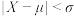 ,
, 及
及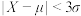 的概率.(结果精确到
的概率.(结果精确到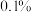 ,
,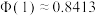 ,
,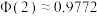 ,
, ).
).
您最近一年使用:0次

 、
、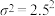 的正态分布.问:随意买一包糖果,其质量误差超过5g(即1%)的可能性有多大?(结果精确到0.1%)
的正态分布.问:随意买一包糖果,其质量误差超过5g(即1%)的可能性有多大?(结果精确到0.1%)


