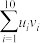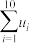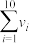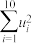1 . 为抓住新一轮科技和产业革命带来的创业机遇,某企业欲购进一批新机床,对现有机床进行更新换代.
(Ⅰ)现有旧机床生产的零件10个,其中直径大于124mm的有3个,若从中随机抽取4个,设 表示取出的零件中直径大于124mm的个数,求
表示取出的零件中直径大于124mm的个数,求 的分布列及数学期望
的分布列及数学期望 ;
;
(Ⅱ)若新机床生产零件的直径(单位:mm)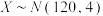 ,从新机床生产的零件中随机抽取10个,求其中至少有1个零件的直径大于124mm的概率.
,从新机床生产的零件中随机抽取10个,求其中至少有1个零件的直径大于124mm的概率.
参考数据:若 ,则
,则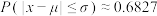 ,
,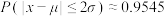 ,
,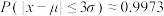 ,
,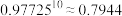 ,
,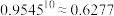 .
.
(Ⅰ)现有旧机床生产的零件10个,其中直径大于124mm的有3个,若从中随机抽取4个,设
 表示取出的零件中直径大于124mm的个数,求
表示取出的零件中直径大于124mm的个数,求 的分布列及数学期望
的分布列及数学期望 ;
;(Ⅱ)若新机床生产零件的直径(单位:mm)
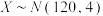 ,从新机床生产的零件中随机抽取10个,求其中至少有1个零件的直径大于124mm的概率.
,从新机床生产的零件中随机抽取10个,求其中至少有1个零件的直径大于124mm的概率.参考数据:若
 ,则
,则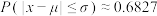 ,
,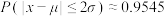 ,
,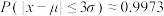 ,
,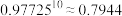 ,
,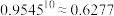 .
.
您最近一年使用:0次
名校
2 . 零部件生产水平是评判一个国家高端装备制造能力的重要标准之一,其中切割加工技术是一项重要技术.某精密仪器制造商研发了一种切割设备,用来生产高精度的机械零件,经过长期生产检验,可以认为该设备生产的零件尺寸服从正态分布 .某机械加工厂购买了该切割设备,在正式投入生产前进行了试生产,从试生产的零件中任意抽取10件作为样本,下面是样本的尺寸
.某机械加工厂购买了该切割设备,在正式投入生产前进行了试生产,从试生产的零件中任意抽取10件作为样本,下面是样本的尺寸 (
(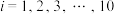 ,单位:
,单位: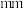 ):
):
用样本的平均数 作为
作为 的估计值,用样本的标准差
的估计值,用样本的标准差 作为
作为 的估计值.
的估计值.
(1)按照技术标准的要求,若样本尺寸均在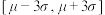 范围内,则认定该设备质量合格,根据数据判断该切割设备的质量是否合格;
范围内,则认定该设备质量合格,根据数据判断该切割设备的质量是否合格;
(2)该机械加工厂将该切割设备投入生产,对生产的零件制订了两种销售方案(假设每种方案对销售量没有影响):
方案1:每个零件均按70元定价销售;
方案2:若零件的实际尺寸在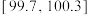 范围内,则该零件为
范围内,则该零件为 级零件,每个零件定价100元,否则为
级零件,每个零件定价100元,否则为 级零件,每个零件定价60元.
级零件,每个零件定价60元.
哪种销售方案的利润更大?请根据数据计算说明.
附: ,样本方差
,样本方差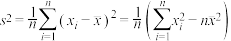 .
.
 .某机械加工厂购买了该切割设备,在正式投入生产前进行了试生产,从试生产的零件中任意抽取10件作为样本,下面是样本的尺寸
.某机械加工厂购买了该切割设备,在正式投入生产前进行了试生产,从试生产的零件中任意抽取10件作为样本,下面是样本的尺寸 (
(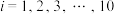 ,单位:
,单位: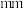 ):
):100.03 | 100.4 | 99.92 | 100.52 | 99.98 |
100.35 | 99.92 | 100.44 | 100.66 | 100.78 |
 作为
作为 的估计值,用样本的标准差
的估计值,用样本的标准差 作为
作为 的估计值.
的估计值.(1)按照技术标准的要求,若样本尺寸均在
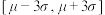 范围内,则认定该设备质量合格,根据数据判断该切割设备的质量是否合格;
范围内,则认定该设备质量合格,根据数据判断该切割设备的质量是否合格;(2)该机械加工厂将该切割设备投入生产,对生产的零件制订了两种销售方案(假设每种方案对销售量没有影响):
方案1:每个零件均按70元定价销售;
方案2:若零件的实际尺寸在
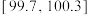 范围内,则该零件为
范围内,则该零件为 级零件,每个零件定价100元,否则为
级零件,每个零件定价100元,否则为 级零件,每个零件定价60元.
级零件,每个零件定价60元.哪种销售方案的利润更大?请根据数据计算说明.
附:
 ,样本方差
,样本方差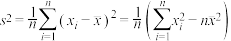 .
.
您最近一年使用:0次
2021-09-23更新
|
514次组卷
|
7卷引用:河南省平顶山市2019-2020学年高二(下)期末数学(理科)试题
3 . 一鲜花店销售某种玫瑰花,根据以往的日销售记录,这种玫瑰花的日销售额(单位:元)服从正态分布 在销售记录中,随机抽取
在销售记录中,随机抽取 天,至少有一天日销售额在
天,至少有一天日销售额在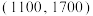 之外的概率约为0.0257.在这
之外的概率约为0.0257.在这 天里,鲜花店老板每天给表现最好的5位员工每位两次抽奖的机会,每次抽奖结果只有“100元和50元”两种结果,由于某种原因,二者出现的概率不一定是等可能的,设出现“100元”的概率为
天里,鲜花店老板每天给表现最好的5位员工每位两次抽奖的机会,每次抽奖结果只有“100元和50元”两种结果,由于某种原因,二者出现的概率不一定是等可能的,设出现“100元”的概率为 ,各次抽奖相互独立.
,各次抽奖相互独立.
(1)求 的值;
的值;
(2)当有10人次参与抽奖时,恰有6人次得到100元的概率为 ,求
,求 的最大值点
的最大值点 ,当
,当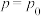 时,设每位员工抽奖得到的金额为
时,设每位员工抽奖得到的金额为 ,预计在这
,预计在这 天里,鲜花店老板需要拿出的抽奖金额的期望是多少?
天里,鲜花店老板需要拿出的抽奖金额的期望是多少?
附:若随机变量 服从正态分布
服从正态分布 ,则
,则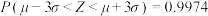 .
.
 在销售记录中,随机抽取
在销售记录中,随机抽取 天,至少有一天日销售额在
天,至少有一天日销售额在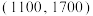 之外的概率约为0.0257.在这
之外的概率约为0.0257.在这 天里,鲜花店老板每天给表现最好的5位员工每位两次抽奖的机会,每次抽奖结果只有“100元和50元”两种结果,由于某种原因,二者出现的概率不一定是等可能的,设出现“100元”的概率为
天里,鲜花店老板每天给表现最好的5位员工每位两次抽奖的机会,每次抽奖结果只有“100元和50元”两种结果,由于某种原因,二者出现的概率不一定是等可能的,设出现“100元”的概率为 ,各次抽奖相互独立.
,各次抽奖相互独立.(1)求
 的值;
的值;(2)当有10人次参与抽奖时,恰有6人次得到100元的概率为
 ,求
,求 的最大值点
的最大值点 ,当
,当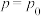 时,设每位员工抽奖得到的金额为
时,设每位员工抽奖得到的金额为 ,预计在这
,预计在这 天里,鲜花店老板需要拿出的抽奖金额的期望是多少?
天里,鲜花店老板需要拿出的抽奖金额的期望是多少?附:若随机变量
 服从正态分布
服从正态分布 ,则
,则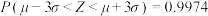 .
.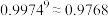 | 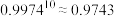 |  | 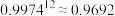 |
您最近一年使用:0次
4 . “公平正义”是构建社会主义和谐社会的重要特征之一,是社会主义法治理念的价值追求.“考试”作为一种公平公正选拔人才的有效途径,正被广泛采用.每次考试过后,考生最关心的问题是:自己的考试名次是多少?自己能否被录取?能获得什么样的职位?
某单位准备通过考试(按照高分优先录取的原则)录用300名职员,其中275个高薪职位和25个普薪职位.实际报名人数为2000名,考试满分为400分(一般地,对于一次成功的考试来说,考试成绩应服从正态分布).考试后考生考试成绩的部分统计结果如下:
考试平均成绩是180分,360分及以上的高分考生有30名.
(1)最低录取分数是多少?(结果保留为整数)
(2)考生甲的成绩为286分,若甲被录取,能否获得高薪职位?若不能被录取,请说明理由.
参考资料:①当 时,令
时,令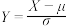 ,则
,则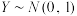 .
.
②当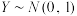 时,
时,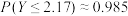 ,
,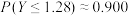 ,
,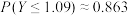 ,
,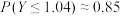 .
.
某单位准备通过考试(按照高分优先录取的原则)录用300名职员,其中275个高薪职位和25个普薪职位.实际报名人数为2000名,考试满分为400分(一般地,对于一次成功的考试来说,考试成绩应服从正态分布).考试后考生考试成绩的部分统计结果如下:
考试平均成绩是180分,360分及以上的高分考生有30名.
(1)最低录取分数是多少?(结果保留为整数)
(2)考生甲的成绩为286分,若甲被录取,能否获得高薪职位?若不能被录取,请说明理由.
参考资料:①当
 时,令
时,令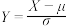 ,则
,则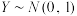 .
.②当
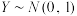 时,
时,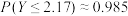 ,
,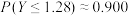 ,
,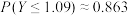 ,
,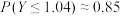 .
.
您最近一年使用:0次
2021-08-26更新
|
196次组卷
|
4卷引用:河南省洛阳市2019-2020学年高三上学期第一次统一考试(1月)数学(理)试题
河南省洛阳市2019-2020学年高三上学期第一次统一考试(1月)数学(理)试题(已下线)专题05 正态分布与原则(第四篇)-备战2020年高考数学大题精做之解答题题型全覆盖山西省怀仁市2020-2021学年高二下学期期中数学(理)试题(已下线)考向42 四大分布:两点分布、二项分布、超几何分布与正态分布(十大经典题型)-3
名校
5 . 某单位招考工作人员,须参加初试和复试,初试通过后组织考生参加复试,共5000人参加复试,复试共三道题,第一题考生答对得3分,答错得0分,后两题考生每答对一道题得5分,答错得0分,答完三道题后的得分之和为考生的复试成绩.
(1)通过分析可以认为参加复试的考生初试成绩 服从正态分布
服从正态分布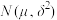 ,其中
,其中 ,
,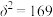 ,试估计这5000人中初试成绩不低于90分的人数;
,试估计这5000人中初试成绩不低于90分的人数;
(2)已知某考生已通过初试,他在复试中第一题答对的概率为 ,后两题答对的概率均为
,后两题答对的概率均为 ,且每道题回答正确与否互不影响.记该考生的复试试成绩为
,且每道题回答正确与否互不影响.记该考生的复试试成绩为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
附:若随机变量 服从正态分布
服从正态分布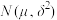 ,则
,则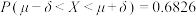 ,
,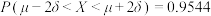 ,
,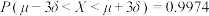 .
.
(1)通过分析可以认为参加复试的考生初试成绩
 服从正态分布
服从正态分布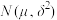 ,其中
,其中 ,
,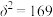 ,试估计这5000人中初试成绩不低于90分的人数;
,试估计这5000人中初试成绩不低于90分的人数;(2)已知某考生已通过初试,他在复试中第一题答对的概率为
 ,后两题答对的概率均为
,后两题答对的概率均为 ,且每道题回答正确与否互不影响.记该考生的复试试成绩为
,且每道题回答正确与否互不影响.记该考生的复试试成绩为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.附:若随机变量
 服从正态分布
服从正态分布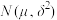 ,则
,则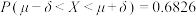 ,
,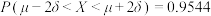 ,
,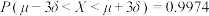 .
.
您最近一年使用:0次
2020-11-27更新
|
3415次组卷
|
17卷引用:河南省郑州市第十一中学2022-2023学年高三上学期1月份线上考试理科数学试题
河南省郑州市第十一中学2022-2023学年高三上学期1月份线上考试理科数学试题江苏省南京市六校联合体2020-2021学年高三上学期11月联考数学试题江苏省南京市第二十九中学2020-2021学年高三上学期期中数学试题江苏省徐州市三校联考2020-2021学年高三上学期期末数学试题重庆市第八中学2021届高三上学期12月阶段性检测(6)数学试题江苏省南京市秦淮中学2021届高三下学期期初学情调研数学试题(已下线)7.5 正态分布(精练)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)安徽省六安市城南中学2020-2021学年高三上学期第三次月考数学(理)试题(已下线)2021届高三高考数学适应性测试八省联考考后仿真系列卷七黑龙江省大庆实验中学实验三部2020-2021学年第一次线上教学质量检测数学(理)试题湖南省益阳市桃江县第一中学2020-2021学年高二(研学班)下学期入学考试数学试题福建省漳州市第三中学2021届高三第五次月考数学科试题河北省衡水中学2021届高三下学期三模数学试题(已下线)数学-2021年高考考前20天终极冲刺攻略(三)(新高考地区专用)【学科网名师堂】(6月3日)(已下线)预测12 概率统计-【临门一脚】2021年高考数学三轮冲刺过关(新高考专用)【学科网名师堂】广东省揭阳市普宁国贤学校2023届高三下学期3月连考3数学试题江苏省郑梁梅高级中学2022-2023学年高二下学期4月月考数学试题
6 . 2020年初,新型冠状病毒肆虐,全民开启防疫防控.冠状肺炎的感染主要是人与人之间进行传播,可以通过飞沫以及粪便进行传染,冠状肺炎感染人群年龄大多数是40岁以上的人群.该病毒进入人体后有潜伏期,潜伏期是指病原体侵入人体至最早出现临床症状的这段时间.潜伏期越长,感染到他人的可能性越高,现对200个病例的潜伏期(单位:天)进行调查,统计发现潜伏期中位数为5,平均数为7.1,方差为5.06.如果认为超过8天的潜伏期属于“长潜伏期”,按照年龄统计样本,得到下面的列联表:
(1)能否有95%的把握认为“长潜伏期”与年龄有关;
(2)假设潜伏期 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .现在很多省份对入境旅客一律要求隔离14天,请用概率的知识解释其合理性;
.现在很多省份对入境旅客一律要求隔离14天,请用概率的知识解释其合理性;
(3)以题目中的样本频率估计概率,设1000个病例中恰有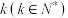 个属于“长潜伏期”的概率是
个属于“长潜伏期”的概率是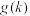 ,当
,当 为何值时,
为何值时,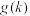 取得最大值?
取得最大值?
附: .
.
若随机变量 服从正态分布
服从正态分布 ,则
,则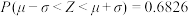 ,
,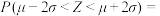
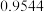 ,
,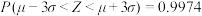 ,
,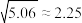 .
.
| 长潜伏期 | 非长潜伏期 | |
40岁以上 | 30 | 110 |
40岁及40岁以下 | 20 | 40 |
(2)假设潜伏期
 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .现在很多省份对入境旅客一律要求隔离14天,请用概率的知识解释其合理性;
.现在很多省份对入境旅客一律要求隔离14天,请用概率的知识解释其合理性;(3)以题目中的样本频率估计概率,设1000个病例中恰有
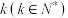 个属于“长潜伏期”的概率是
个属于“长潜伏期”的概率是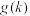 ,当
,当 为何值时,
为何值时,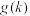 取得最大值?
取得最大值?附:
 .
. | 0.1 | 0.05 | 0.010 |
 | 2.706 | 3.841 | 6.635 |
 服从正态分布
服从正态分布 ,则
,则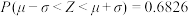 ,
,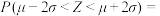
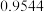 ,
,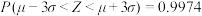 ,
,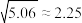 .
.
您最近一年使用:0次
7 . 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如图的频率分布直方图:
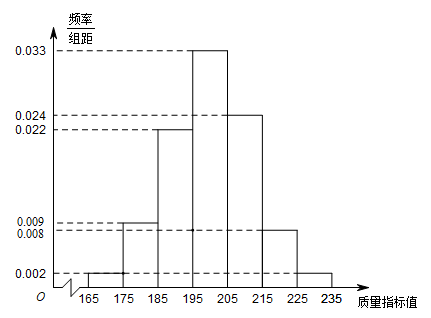
(1)求这500件产品质量指标值的样本平均数 和样本方差
和样本方差 (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(2)由频率分布直方图可以认为,这种产品的质量指标值 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .
.
(i)利用该正态分布,求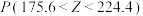 ;
;
(ii)某用户从该企业购买了200件这种产品,记X表示这200件产品中质量指标值位于区间 的产品件数,利用(i)的结果,求
的产品件数,利用(i)的结果,求 .
.
附: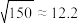 .若
.若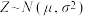 ,则
,则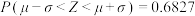 ,
,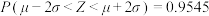 .
.

(1)求这500件产品质量指标值的样本平均数
 和样本方差
和样本方差 (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);(2)由频率分布直方图可以认为,这种产品的质量指标值
 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .
.(i)利用该正态分布,求
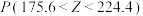 ;
;(ii)某用户从该企业购买了200件这种产品,记X表示这200件产品中质量指标值位于区间
 的产品件数,利用(i)的结果,求
的产品件数,利用(i)的结果,求 .
.附:
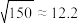 .若
.若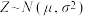 ,则
,则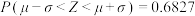 ,
,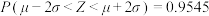 .
.
您最近一年使用:0次
名校
解题方法
8 . 当前,全球贸易格局发生重大变化,随着中美贸易战的不断升级,让越来越多的中国科技企业开始意识到自主创新的重要性,大大加强科技研发投入的力度,形成掌控高新尖端核心技术及其市场的能力.某企业为确定下一年对某产品进行科技升级的研发费用,需了解该产品年研发费用 (单位:千万元)对年销售量
(单位:千万元)对年销售量 (单位:千万件)和年利润
(单位:千万件)和年利润 (单位:千万元)的影响.根据市场调研与模拟,对收集的数据
(单位:千万元)的影响.根据市场调研与模拟,对收集的数据 进行初步处理,得到散点图及一些统计量的值如下:
进行初步处理,得到散点图及一些统计量的值如下:
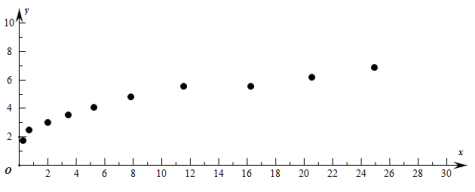
表中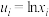 ,
,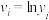 .
.
(1)根据散点图判断, 与
与 哪一个更适合作为年销售量
哪一个更适合作为年销售量 关于年研发费用
关于年研发费用 的回归方程类型(给出判断即可,不必说明理由),并根据判断结果及表中数据,建立
的回归方程类型(给出判断即可,不必说明理由),并根据判断结果及表中数据,建立 关于
关于 的回归方程;
的回归方程;
附:对于一组数据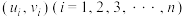 ,其回归直线
,其回归直线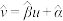 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为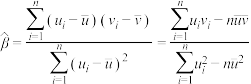 ,
, .
.
(2)已知年利润 与
与 ,
, 的关系为
的关系为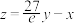 (其中
(其中 为自然对数的底数),要使企业下一年的年利润最大,预计下一年应投入多少研发费用?
为自然对数的底数),要使企业下一年的年利润最大,预计下一年应投入多少研发费用?
(3)科技升级后,该产品的效率 大幅提高,经试验统计得
大幅提高,经试验统计得 大致服从正态分布
大致服从正态分布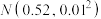 .企业对科技升级团队的奖励方案如下:若
.企业对科技升级团队的奖励方案如下:若 不超过
不超过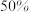 ,不予奖励;若
,不予奖励;若 超过
超过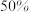 ,但不超过
,但不超过 ,每件产品奖励2元;若
,每件产品奖励2元;若 超过
超过 ,每件产品奖励4元.记
,每件产品奖励4元.记 为每件产品获得的奖励,求
为每件产品获得的奖励,求 (精确到0.01).
(精确到0.01).
附:若随机变量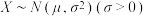 ,则
,则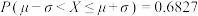 ,
,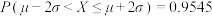 .
.
 (单位:千万元)对年销售量
(单位:千万元)对年销售量 (单位:千万件)和年利润
(单位:千万件)和年利润 (单位:千万元)的影响.根据市场调研与模拟,对收集的数据
(单位:千万元)的影响.根据市场调研与模拟,对收集的数据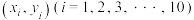 进行初步处理,得到散点图及一些统计量的值如下:
进行初步处理,得到散点图及一些统计量的值如下:
|
|
|
|
30.5 | 15 | 15 | 46.5 |
表中
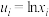 ,
,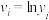 .
.(1)根据散点图判断,
 与
与 哪一个更适合作为年销售量
哪一个更适合作为年销售量 关于年研发费用
关于年研发费用 的回归方程类型(给出判断即可,不必说明理由),并根据判断结果及表中数据,建立
的回归方程类型(给出判断即可,不必说明理由),并根据判断结果及表中数据,建立 关于
关于 的回归方程;
的回归方程;附:对于一组数据
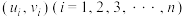 ,其回归直线
,其回归直线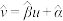 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为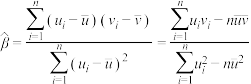 ,
, .
.(2)已知年利润
 与
与 ,
, 的关系为
的关系为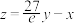 (其中
(其中 为自然对数的底数),要使企业下一年的年利润最大,预计下一年应投入多少研发费用?
为自然对数的底数),要使企业下一年的年利润最大,预计下一年应投入多少研发费用?(3)科技升级后,该产品的效率
 大幅提高,经试验统计得
大幅提高,经试验统计得 大致服从正态分布
大致服从正态分布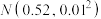 .企业对科技升级团队的奖励方案如下:若
.企业对科技升级团队的奖励方案如下:若 不超过
不超过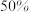 ,不予奖励;若
,不予奖励;若 超过
超过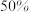 ,但不超过
,但不超过 ,每件产品奖励2元;若
,每件产品奖励2元;若 超过
超过 ,每件产品奖励4元.记
,每件产品奖励4元.记 为每件产品获得的奖励,求
为每件产品获得的奖励,求 (精确到0.01).
(精确到0.01).附:若随机变量
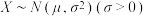 ,则
,则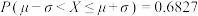 ,
,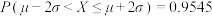 .
.
您最近一年使用:0次
2020-07-14更新
|
408次组卷
|
2卷引用:河南省开封市2020届高三第三次模拟考试数学(理)试题
9 . 在市高二下学期期中考试中,理科学生的数学成绩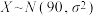 ,已知
,已知 ,则从全市理科生中任选一名学生,他的数学成绩小于110分的概率为( )
,则从全市理科生中任选一名学生,他的数学成绩小于110分的概率为( )
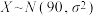 ,已知
,已知 ,则从全市理科生中任选一名学生,他的数学成绩小于110分的概率为( )
,则从全市理科生中任选一名学生,他的数学成绩小于110分的概率为( )| A.0.15 | B.0.50 | C.0.70 | D.0.85 |
您最近一年使用:0次
2020-10-14更新
|
1737次组卷
|
4卷引用:河南省洛阳市2018-2019学年高二5月期末数学(理)试题
名校
10 . 为进一步深化“平安校园”创建活动,加强校园安全教育宣传,某高中对该校学生进行了安全教育知识测试(满分100分),并从中随机抽取了200名学生的成绩,经过数据分析得到如图1所示的频数分布表,并绘制了得分在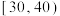 以及
以及 的茎叶图,分别如图2、3所示.
的茎叶图,分别如图2、3所示.

(1)求这200名同学得分的平均数;(同组数据用区间中点值作代表)
(2)如果变量 满足
满足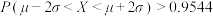 且
且 ,则称变量
,则称变量 “近似满足正态分布
“近似满足正态分布 的概率分布”.经计算知样本方差为210,现在取
的概率分布”.经计算知样本方差为210,现在取 和
和 分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布
分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布 的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
(3)学校决定对90分及以上的同学进行奖励,为了体现趣味性,采用抽奖的方式进行,其中得分不低于94的同学有两次抽奖机会,低于94的同学只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为:
现在从不低于90同学中随机选一名同学,记其获奖金额为 ,以样本估计总体,将频率视为概率,求
,以样本估计总体,将频率视为概率,求 的分布列和数学期望.
的分布列和数学期望.
(参考数据: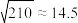 )
)
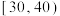 以及
以及 的茎叶图,分别如图2、3所示.
的茎叶图,分别如图2、3所示.成绩 | 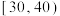 | 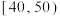 |  |  |  |  |  |
频数 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
图1

(1)求这200名同学得分的平均数;(同组数据用区间中点值作代表)
(2)如果变量
 满足
满足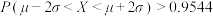 且
且 ,则称变量
,则称变量 “近似满足正态分布
“近似满足正态分布 的概率分布”.经计算知样本方差为210,现在取
的概率分布”.经计算知样本方差为210,现在取 和
和 分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布
分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布 的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.(3)学校决定对90分及以上的同学进行奖励,为了体现趣味性,采用抽奖的方式进行,其中得分不低于94的同学有两次抽奖机会,低于94的同学只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为:
奖金 | 50 | 100 |
概率 |  |  |
 ,以样本估计总体,将频率视为概率,求
,以样本估计总体,将频率视为概率,求 的分布列和数学期望.
的分布列和数学期望.(参考数据:
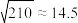 )
)
您最近一年使用:0次
2020-05-25更新
|
508次组卷
|
3卷引用:河南省信阳市2020-2021学年高三上学期期末数学(理科)试题