名校
1 . 如图, 病人服下一粒某种退烧药后, 每毫升血液中含药量  (微克) 与时间
(微克) 与时间 (小时)之间的关系满足: 前 5 个小时按函数
(小时)之间的关系满足: 前 5 个小时按函数 递增, 后 5 个小时
递增, 后 5 个小时 随着时间
随着时间 变化的图像是一条线段.
变化的图像是一条线段.
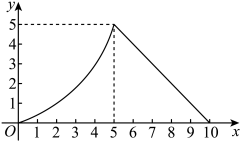
(1)求 关于
关于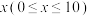 的函数关系式;
的函数关系式;
(2)已知每毫升血液中含药量不低于 3 微克时有治疗效果, 含药量低于 3 微克时无治疗效果, 试问病人服下一粒该退烧药后有治疗效果的时间为多少小时?
 (微克) 与时间
(微克) 与时间 (小时)之间的关系满足: 前 5 个小时按函数
(小时)之间的关系满足: 前 5 个小时按函数 递增, 后 5 个小时
递增, 后 5 个小时 随着时间
随着时间 变化的图像是一条线段.
变化的图像是一条线段.
(1)求
 关于
关于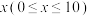 的函数关系式;
的函数关系式;(2)已知每毫升血液中含药量不低于 3 微克时有治疗效果, 含药量低于 3 微克时无治疗效果, 试问病人服下一粒该退烧药后有治疗效果的时间为多少小时?
您最近一年使用:0次
2022-12-20更新
|
454次组卷
|
4卷引用:宁夏银川市贺兰县第一中学2022-2023学年高一上学期期末考试数学试题
名校
2 . 学校计划将花坛改造为一个容积为8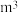 长方体无盖喷泉池,池底每1
长方体无盖喷泉池,池底每1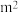 的造价为120元,池壁每1
的造价为120元,池壁每1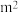 的造价为100元,
的造价为100元,
(1)若池底周长为12 ,设矩形池底的一条边长为x,现要求池深不超过1
,设矩形池底的一条边长为x,现要求池深不超过1 ,问池底的边长x应控制在什么范围内?
,问池底的边长x应控制在什么范围内?
(2)若深为0.5 ,问怎么设计喷泉池底能使总价最低,最低总价是多少?
,问怎么设计喷泉池底能使总价最低,最低总价是多少?
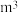 长方体无盖喷泉池,池底每1
长方体无盖喷泉池,池底每1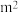 的造价为120元,池壁每1
的造价为120元,池壁每1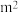 的造价为100元,
的造价为100元,(1)若池底周长为12
 ,设矩形池底的一条边长为x,现要求池深不超过1
,设矩形池底的一条边长为x,现要求池深不超过1 ,问池底的边长x应控制在什么范围内?
,问池底的边长x应控制在什么范围内?(2)若深为0.5
 ,问怎么设计喷泉池底能使总价最低,最低总价是多少?
,问怎么设计喷泉池底能使总价最低,最低总价是多少?
您最近一年使用:0次
2022-11-11更新
|
239次组卷
|
3卷引用:宁夏银川市贺兰县景博中学2022-2023学年高一上学期期中考试数学试题



