解题方法
1 . 设函数 ,若函数
,若函数 在
在 上是增函数,则
上是增函数,则 的取值范围是
的取值范围是___________ .
 ,若函数
,若函数 在
在 上是增函数,则
上是增函数,则 的取值范围是
的取值范围是
您最近半年使用:0次
解题方法
2 . 如图,在面积为 的
的 中,M,N分别为
中,M,N分别为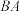 ,
,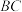 的中点,点P在
的中点,点P在 上,若
上,若 ,则
,则 的最小值是
的最小值是________ .
 的
的 中,M,N分别为
中,M,N分别为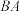 ,
,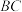 的中点,点P在
的中点,点P在 上,若
上,若 ,则
,则 的最小值是
的最小值是
您最近半年使用:0次
2024高三·全国·专题练习
3 . 已知不等式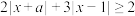 的解集为
的解集为 .
.
(1)求实数 的取值范围;
的取值范围;
(2)若 为负实数,且
为负实数,且 的最大值为
的最大值为 ,正实数
,正实数 ,
, 满足
满足 ,证明:
,证明: .
.
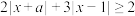 的解集为
的解集为 .
.(1)求实数
 的取值范围;
的取值范围;(2)若
 为负实数,且
为负实数,且 的最大值为
的最大值为 ,正实数
,正实数 ,
, 满足
满足 ,证明:
,证明: .
.
您最近半年使用:0次
2024·全国·模拟预测
解题方法
4 . 已知函数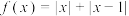 .
.
(1)求不等式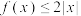 的解集;
的解集;
(2)若 的最小值为t,
的最小值为t, ,
, ,求
,求 的最小值.
的最小值.
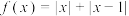 .
.(1)求不等式
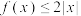 的解集;
的解集;(2)若
 的最小值为t,
的最小值为t, ,
, ,求
,求 的最小值.
的最小值.
您最近半年使用:0次
名校
解题方法
5 . 设 .
.
(1)若不等式 对一切实数x恒成立,求实数m的取值范围;
对一切实数x恒成立,求实数m的取值范围;
(2)在(1)的条件下,求 的最小值;
的最小值;
(3)解关于x的不等式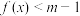 .
.
 .
.(1)若不等式
 对一切实数x恒成立,求实数m的取值范围;
对一切实数x恒成立,求实数m的取值范围;(2)在(1)的条件下,求
 的最小值;
的最小值;(3)解关于x的不等式
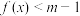 .
.
您最近半年使用:0次
6 . 在平面直角坐标系 中,一动圆经过点
中,一动圆经过点 且与直线
且与直线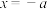 相切,设该动圆圆心的轨迹为曲线K, P是曲线K上一点.
相切,设该动圆圆心的轨迹为曲线K, P是曲线K上一点.
(1)当 时,求曲线K的轨迹方程;
时,求曲线K的轨迹方程;
(2)已知过点A 且斜率为k的直线l与曲线K交于B,C 两点,若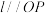 且直线
且直线 与直线
与直线 交于Q点.求证:
交于Q点.求证:  为定值:
为定值:
(3)若
 且点 D,E在y轴上,
且点 D,E在y轴上, 的内切圆的方程为
的内切圆的方程为
 求
求 面积的最小值.
面积的最小值.
 中,一动圆经过点
中,一动圆经过点 且与直线
且与直线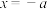 相切,设该动圆圆心的轨迹为曲线K, P是曲线K上一点.
相切,设该动圆圆心的轨迹为曲线K, P是曲线K上一点.(1)当
 时,求曲线K的轨迹方程;
时,求曲线K的轨迹方程;(2)已知过点A 且斜率为k的直线l与曲线K交于B,C 两点,若
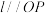 且直线
且直线 与直线
与直线 交于Q点.求证:
交于Q点.求证:  为定值:
为定值:(3)若

 且点 D,E在y轴上,
且点 D,E在y轴上, 的内切圆的方程为
的内切圆的方程为
 求
求 面积的最小值.
面积的最小值.
您最近半年使用:0次
解题方法
7 . 在 中,角A,B,C所对的边分别为a,b,c,若
中,角A,B,C所对的边分别为a,b,c,若 ,则
,则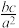 的最大值为( )
的最大值为( )
 中,角A,B,C所对的边分别为a,b,c,若
中,角A,B,C所对的边分别为a,b,c,若 ,则
,则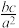 的最大值为( )
的最大值为( )A. | B. | C. | D.3 |
您最近半年使用:0次
解题方法
8 . 若 ,则
,则 的最小值是( )
的最小值是( )
 ,则
,则 的最小值是( )
的最小值是( )A. | B. | C.4 | D.2 |
您最近半年使用:0次
9 . 如图, 是边长为2的正方形纸片,沿某动直线
是边长为2的正方形纸片,沿某动直线 为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点
为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点 都落在边
都落在边 上,记为
上,记为 ;折痕
;折痕 与
与 交于点
交于点 ,点
,点 满足关系式
满足关系式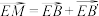 .以点
.以点 为坐标原点建立坐标系,若曲线
为坐标原点建立坐标系,若曲线 是由点
是由点 的轨迹及其关于边
的轨迹及其关于边 对称的曲线组成的,等腰梯形
对称的曲线组成的,等腰梯形 的
的 分别与曲线
分别与曲线 切于点P、Q、
切于点P、Q、 ,且
,且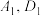 在x轴上.则梯形
在x轴上.则梯形 的面积最小值为( )
的面积最小值为( )
 是边长为2的正方形纸片,沿某动直线
是边长为2的正方形纸片,沿某动直线 为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点
为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点 都落在边
都落在边 上,记为
上,记为 ;折痕
;折痕 与
与 交于点
交于点 ,点
,点 满足关系式
满足关系式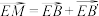 .以点
.以点 为坐标原点建立坐标系,若曲线
为坐标原点建立坐标系,若曲线 是由点
是由点 的轨迹及其关于边
的轨迹及其关于边 对称的曲线组成的,等腰梯形
对称的曲线组成的,等腰梯形 的
的 分别与曲线
分别与曲线 切于点P、Q、
切于点P、Q、 ,且
,且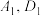 在x轴上.则梯形
在x轴上.则梯形 的面积最小值为( )
的面积最小值为( )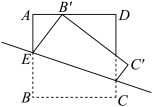
| A.6 | B. | C.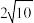 | D. |
您最近半年使用:0次
解题方法
10 . 已知 为锐角,且
为锐角,且 ,则
,则 的最大值为( )
的最大值为( )
 为锐角,且
为锐角,且 ,则
,则 的最大值为( )
的最大值为( )A.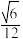 | B.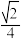 | C.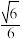 | D. |
您最近半年使用:0次



