名校
解题方法
1 . 若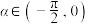 ,且
,且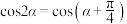 ,则
,则
__________ .
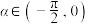 ,且
,且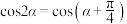 ,则
,则
您最近一年使用:0次
昨日更新
|
690次组卷
|
3卷引用:湖北省部分学校2025届高三上学期第一次大联考(一模)数学试题
2 . 已知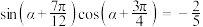 ,则
,则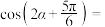 ( )
( )
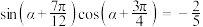 ,则
,则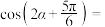 ( )
( )A. | B. | C. | D.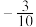 |
您最近一年使用:0次
名校
解题方法
3 . 已知 为锐角,
为锐角,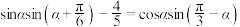 ,则
,则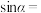 ( )
( )
 为锐角,
为锐角,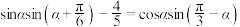 ,则
,则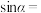 ( )
( )A.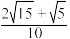 | B.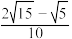 | C. | D.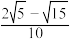 |
您最近一年使用:0次
7日内更新
|
546次组卷
|
3卷引用:重庆市拔尖强基联盟2025届高三上学期10月联合考试数学试卷
重庆市拔尖强基联盟2025届高三上学期10月联合考试数学试卷吉林省通化市梅河口市第五中学2025届高三上学期10月月考数学试题(已下线)考点33 诱导公式的应用 --高考数学100个黄金考点(2025届)【讲】
名校
解题方法
4 . 已知 为锐角,
为锐角,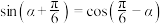 ,则
,则 ( ).
( ).
 为锐角,
为锐角,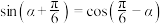 ,则
,则 ( ).
( ).A. | B.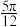 | C. | D.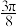 |
您最近一年使用:0次
名校
5 . 已知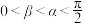 ,
, ,
, ,则
,则
______ .
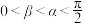 ,
, ,
, ,则
,则
您最近一年使用:0次
7日内更新
|
426次组卷
|
2卷引用:山东省泰安第一中学2024-2025学年高三上学期10月月考数学试题
名校
解题方法
6 . 已知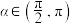 ,
,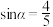 ,则
,则
____________ .
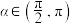 ,
,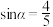 ,则
,则
您最近一年使用:0次
名校
解题方法
7 . 已知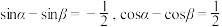 ,且
,且 均为锐角,则
均为锐角,则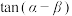 的值等于
的值等于______________
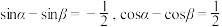 ,且
,且 均为锐角,则
均为锐角,则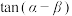 的值等于
的值等于
您最近一年使用:0次
名校
8 . 已知 ,
,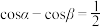 ,则
,则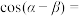 ( )
( )
 ,
,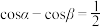 ,则
,则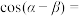 ( )
( )A.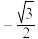 | B. | C. | D. |
您最近一年使用:0次
名校
9 . 已知 ,则
,则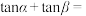 ( )
( )
 ,则
,则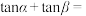 ( )
( )A. | B. | C.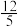 | D.12 |
您最近一年使用:0次
7日内更新
|
1246次组卷
|
2卷引用:浙江省嘉兴市2024-2025学年高三上学期9月基础测试数学试题
解题方法
10 . 已知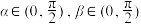 .
.
(1)若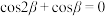 ,
,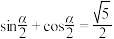 ,求
,求 的值;
的值;
(2)证明: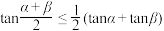 .
.
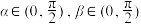 .
.(1)若
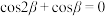 ,
,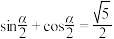 ,求
,求 的值;
的值;(2)证明:
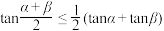 .
.
您最近一年使用:0次
7日内更新
|
265次组卷
|
2卷引用:江苏省淮安市十校2024-2025学年高三上学期第一次联考数学试题



